Zusammenhangsmaß

Ein Zusammenhangsmaß oder auch Assoziationsmaß genannt, gibt in der Statistik die Stärke und gegebenenfalls die Richtung eines Zusammenhangs zweier statistischer Variablen wieder.

Allgemeines

Je nach Voraussetzung gibt es einen oder mehrere mögliche Zusammenhangsmaße, z.B.

abhängig vom Skalenniveau der Merkmale oder Zufallsvariablen: kategorial (nominal, ordinal) oder metrisch und
abhängig davon, ob man ein standardisiertes oder ein nicht-standardisiertes Maß verwenden möchte.

Als nicht-standardisierte Zusammenhangsmaße werden solche bezeichnet, die ausschließlich für Tabellen gleicher Dimension und/oder bei gleichem Stichprobenumfang vergleichbar sind. Diese Maße nehmen in der Regel den Wert null an, wenn keine Abhängigkeit zwischen den betrachteten Merkmalen vorliegt. Standardisierte Zusammenhangsmaße nehmen Werte in einem Intervall an; damit kann man auch die Stärke des Zusammenhangs beurteilen.

Standardisierte Zusammenhangsmaße, bei denen mindestens ein Merkmal nominal skaliert ist, nehmen meist nur Werte im Intervall [0;1] an. Sind beide Merkmale mindestens ordinal skaliert, dann nehmen die standardisierten Zusammenhangsmaße Werte in Intervall [-1;1] (Fall 1) oder [0;1] (Fall 2) an. Im ersten Fall wird neben der Stärke des Zusammenhangs auch eine Richtung angegeben.

Zum zweiten Fall zählen auch die Fehlerreduktionsmaße. Hier wird vorausgesetzt, dass ein Vorhersagewert für die abhängige Variable berechnet werden kann. Einmal unter Kenntnis des Zusammenhangs (je nach Wert/Kategorie der unabhängigen Variablen sage ich einen bestimmten Wert/Kategorie der abhängigen Variablen voraus) und einmal ohne Kenntnis des Zusammenhangs (nur basierend auf den Werten/Kategorien der abhängigen Variablen). Danach wird die Reduktion des Vorhersagefehlers bei beiden Methoden betrachtet. Damit wird der Zusammenhang zwischen den Variablen indirekt quantifiziert. Dies führt auch zu asymmetrischen Maßzahlen, je nachdem welche der beiden Variablen die abhängige Variable ist. Asymmetrisch bedeutet hier, dass sich der Wert des Koeffizienten ändert, wenn man statt der Beobachtungsreihe (x_i, y_i) die Beobachtungsreihe $(y_{i},x_{i})$ betrachtet.

Koeffizienten

Für zwei nominale Variablen

→ >Hauptartikel: Kontingenzkoeffizient

Bei Koeffizienten für zwei nominal skalierten Variablen liegt eine Kontingenztabelle mit den gemeinsamen Häufigkeiten (bzw. Wahrscheinlichkeiten für Zufallsvariablen) zugrunde. Für die direkte Messung des Zusammenhang wird die quadratische Kontingenz verwendet, die die beobachten gemeinsamen Häufigkeiten mit den erwarteten gemeinsamen Häufigkeiten unter Unabhängigkeit (= kein Zusammenhang) vergleicht. Weichen die beiden Häufigkeiten für eine oder mehrere Kombinationen von Merkmalsausprägungen voneinander ab, dann liegt ein Zusammenhang vor. Des Weiteren gibt es spezielle Koeffizienten für 2x2-Kontingenztabellen. Zusammenhangsmaße für nominale Variablen können auch für ordinale oder metrisch diskrete Merkmale eingesetzt werden. Allerdings wird dabei ein Teil der Information in den Daten, z.B. die Rangfolge der Merkmalsausprägungen, nicht ausgenutzt.

Koeffizient	Wertebereich	Bemerkung
Quadratische Kontingenz	größer gleich null	nicht-standardisiert, symmetrisch
Mittlere quadratische Kontingenz	größer gleich null	standardisiert für 2x2-Kontingenztabellen, symmetrisch
Kontingenzkoeffizient	größer gleich null und kleiner als eins	nicht-standardisiert, symmetrisch
Korrigierter Kontingenzkoeffizient	im Intervall	standardisiert, symmetrisch
Cramérs V	im Intervall (?)	standardisiert, symmetrisch
Phi-Koeffizient	im Intervall (?)	standardisiert, symmetrisch, Spezialfall von Cramérs V für 2x2-Kontingenztabellen
Chancenverhältnis	größer gleich null	nicht-standardisiert, asymmetrisch, meist für 2x2-Kontingenztabellen
Goodman und Kruskals Lambda	im Intervall	standardisiert, symmetrisch und asymmetrisch, Fehlerreduktionsmaß
Goodman und Kruskals Tau	im Intervall	standardisiert, symmetrisch und asymmetrisch, Fehlerreduktionsmaß
Unsicherheitskoeffizient	im Intervall	standardisiert, symmetrisch und asymmetrisch, Fehlerreduktionsmaß

Für zwei ordinale Variablen

Bei Koeffizienten für zwei ordinal skalierte Variablen wird die Zahl der Beobachtungspaare $(x_{i},y_{i}),(x_{j},y_{j})$ ermittelt, die konkordant ( $x_{i}<x_{j}$ und $y_{i}<y_{j}$ ) bzw. diskordant ( $x_{i}<x_{j}$ und $y_{i}>y_{j}$ ) sind. Konkordante Paare sprechen eher für einen positiven Zusammenhang, d.h. bei den Beobachtungen treten kleine Werte von mit kleinen Werten von und große Werte von mit großen Werten von auf. Diskordante Paare sprechen eher für einen negativen Zusammenhang, d.h. bei den Beobachtungen treten kleine Werte von mit großen Werten von und große Werte von mit kleinen Werten von auf. Aus der Zahl der konkordanten und diskordanten wird dann ein Zusammenhangsmaß berechnet. Die einzelnen Koeffizienten unterscheiden sich dann in der Art und Weise wie Bindungen, d.h. Beobachtungspaare mit $x_{i}=x_{j}$ und/oder $y_{i}=y_{j}$ berücksichtigt werden.

Eine Alternative ist die Verwendung von Rängen. Hierbei wird jedem Beobachtungswert $x_{i}$ ein Rang zugeordnet, der seiner Position in der sortierten Reihe der Werte angibt. Das Gleiche geschieht mit den -Werten. Dann wird für jede Beobachtung der Rang von $x_{i}$ mit dem Rang von $y_{i}$ verglichen. Je stärker die Ränge bei einer Beobachtung übereinstimmen, desto mehr spricht es für einen positiven Zusammenhang. Je stärker sich die Ränge bei einer Beobachtung unterscheiden, desto mehr spricht es für einen negativen Zusammenhang.

Zusammenhangsmaße für ordinale Variablen können auch für metrisch Merkmale eingesetzt werden. Auch hierbei wird dann ein Teil der Information in den Daten nicht ausgenutzt, andererseits sind diese Koeffizienten dann robust gegen Ausreißer und zeigen auch nicht-linearen Zusammenhänge an.

Koeffizient	Wertebereich	Bemerkung
Kovarianz für Rangplätze	im Intervall $\left[-{\tfrac {n(n-1)}{2}};+{\tfrac {n(n-1)}{2}}\right]$	nicht-standardisiert, symmetrisch, Differenz der konkordanten und diskordanten Paare
Kendall’sches Tau a	im Intervall	standardisiert, symmetrisch, berücksichtigt keine Bindungen
Kendall’sches Tau b	im Intervall	standardisiert, symmetrisch, berücksichtigt keine Beobachtungspaare mit $x_{i}=x_{j}$ und $y_{i}=y_{j}$ , erreicht die Werte und auf nicht-quadratischen Tabellen nicht
Kendall’sches Tau c	im Intervall	standardisiert, symmetrisch, berücksichtigt keine Bindungen, korrigiert aber für nicht-quadratischen Tabellen
Kendall’sches Tau	im Intervall	standardisiert, symmetrisch, berücksichtigt keine Beobachtungspaare mit $x_{i}=x_{j}$ und $y_{i}=y_{j}$
Goodman und Kruskals Gamma	im Intervall	standardisiert, symmetrisch, weist beim Vorliegen von Bindungen zu hohe Werte auf, der Absolutbetrag ist ein Fehlerreduktionsmaß
Yule's Q	im Intervall	standardisiert, symmetrisch, Spezialfall von Goodman und Kruskals Gamma für dichotome Variablen, kann auch für nominale Variablen eingesetzt werden
Spearman’scher Rangkorrelationskoeffizient	im Intervall	standardisiert, symmetrisch, setzt implizit voraus, dass benachbarte Ränge immer den gleichen Abstand haben

Für zwei metrische Variablen

Konstruktion der Kovarianz: $s_{{xy}}:={\frac 1n}\sum _{{i=1}}^{n}(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})$

Bei Koeffizienten für zwei metrisch skalierte Variablen wird für jede Beobachtung der Abstand von $x_{i}$ zu einem Mittelwert der Werte sowie der Abstand von $y_{i}$ zu einem Mittelwert der Werte ermittelt. Danach wird für jede Beobachtung das Produkt der beiden Abstände berechnet und über alle Beobachtungen gemittelt. 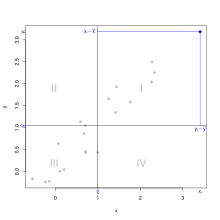Positive Werte des Produktes sprechen für einen positiven Zusammenhang, negative Werte für einen negativen Zusammenhang. Die Grafik rechts zeigt dies für die Kovarianz einer Beobachtungsreihe: Für jede Beobachtung wird der Abstand zum Mittelwert ermittelt, dann multipliziert und gemittelt. Die Koeffizienten unterscheiden sich darin wie der Abstand berechnet wird und welcher Mittelwert verwendet wird (arithmetisches Mittel oder Median).

Auch der Spearmans Rangkorrelationskoeffizient folgt diesem Schema, statt $x_{i}$ und $y_{i}$ werden die Ränge von $x_{i}$ und $y_{i}$ in der Bravais-Pearson-Korrelation verwendet. Durch die Eigenschaften der Ränge, z.B. $\textstyle \sum _{i=1}^{n}\operatorname {Rang} (x_{i})={\tfrac {n(n+1)}{2}}$ , kann die Formel der Bravais-Pearson-Korrelation vereinfacht werden.

Koeffizient	Wertebereich	Bemerkung
Kovarianz	im Intervall $(-\infty ;+\infty )$	nicht-standardisiert, symmetrisch, nicht robust, misst nur den linearen Zusammenhang
Bravais-Pearson-Korrelation	im Intervall	standardisiert, symmetrisch, nicht robust, misst nur den linearen Zusammenhang
Quadrantenkorrelation	im Intervall	standardisiert, symmetrisch, robust, misst auch nicht-lineare Zusammenhänge
Bestimmtheitsmaß	im Intervall	standardisiert, symmetrisch, nicht robust, Fehlerreduktionsmaß

Für zwei Variablen unterschiedlichen Skalenniveaus

Eine oft genutzte Möglichkeit ist die Benutzung eines Koeffizienten, der für zwei Variablen des niedrigen Skalenniveaus geeignet ist. Ist z.B. eine Variable ordinal, die andere metrisch skaliert, dann benutzt man einen Koeffizienten für zwei ordinale Variablen. Dabei nimmt man in Kauf, dass man nicht alle Informationen in den Beobachtungen ausnutzt.

Sehr problematisch wird dies, wenn eine Variable metrisch (stetig) ist und die andere nominal. Daher wurden eine Reihe von speziellen Koeffizienten für unterschiedliche Skalenniveaus entwickelt. Eine Vertauschung der Rollen der Variablen in den Formeln ist nicht möglich, d.h. es ergibt keinen Sinn, von symmetrischen oder asymmetrischen Koeffizienten zu sprechen.

Koeffizient			Wertebereich	Bemerkung
Eta Quadrat	nominal	metrisch	im Intervall	Fehlerreduktionsmaß, nicht robust
Punktbiseriale Korrelation	dichotom	metrisch	im Intervall	nicht robust

Basierend auf einem Artikel in:

Wikipedia.de