Multiple lineare Regression

In der Statistik ist die multiple lineare Regression, auch mehrfache lineare Regression (kurz: MLR) oder lineare Mehrfachregression genannt, ein regressionsanalytisches Verfahren und ein Spezialfall der linearen Regression. Die multiple lineare Regression ist ein statistisches Verfahren, mit dem versucht wird, eine beobachtete abhängige Variable durch mehrere unabhängige Variablen zu erklären. Das dazu verwendete Modell ist linear in den Parametern, wobei die abhängige Variable eine Funktion der unabhängigen Variablen ist. Diese Beziehung wird durch eine additive Störgröße überlagert. Die multiple lineare Regression stellt eine Verallgemeinerung der einfachen linearen Regression bzgl. der Anzahl der Regressoren dar.

Das klassische Modell der linearen Mehrfachregression

Im Folgenden wird von linearen Funktionen ausgegangen. Es ist dann keine weitere Beschränkung der Allgemeinheit, dass diese Funktionen direkt aus den unabhängigen (erklärenden, exogenen) Variablen bestehen und es ebenso viele zu schätzende Regressionsparameter $\beta _{k}$ gibt wie unabhängige Variablen $x_{k}$ (Index $k=1,2,\dots ,K$ ). Zum Vergleich: In der einfachen linearen Regression ist K=2 und $x_{1}$ konstant gleich , der zugehörige Regressionsparameter also der Achsenabschnitt.

Das Modell für Messungen der abhängigen (endogenen) Variablen ist also

$y_{t}=x_{t1}\beta _{1}+x_{t2}\beta _{2}+\ldots +x_{tK}\beta _{K}+\varepsilon _{t}$ ,

mit Störgrößen $\varepsilon _{t}$ , die rein zufällig sind, falls das lineare Modell passt. Für das Modell wird weiterhin angenommen, dass die Gauß-Markow-Annahmen gelten. In einem stichprobentheoretischen Ansatz wird jedes Stichprobenelement $\varepsilon _{t}$ als eine eigene Zufallsvariable interpretiert, ebenso jedes y_t .

Liegen die Daten

$(y_{1};x_{11},\dotsc ,x_{1K}),(y_{2};x_{21},\dotsc ,x_{2K}),\dotsc ,(y_{T};x_{T1},\dotsc ,x_{TK})$

vor, so ergibt sich folgendes lineare Gleichungssystem:

${\begin{matrix}y_{1}=x_{11}\beta _{1}+x_{12}\beta _{2}\,+&\dotsb &+\,x_{1K}\beta _{K}+\varepsilon _{1}\\y_{2}=x_{21}\beta _{1}+x_{22}\beta _{2}\,+&\dotsb &+\,x_{2K}\beta _{K}+\varepsilon _{2}\\&\vdots &\\y_{T}=x_{T1}\beta _{1}+x_{T2}\beta _{2}\,+&\dotsb &+\,x_{TK}\beta _{K}+\varepsilon _{T}\\\end{matrix}}$

Das multiple lineare Regressionsmodell (selten und doppeldeutig allgemeines lineares Modell) lässt sich in Matrixschreibweise wie folgt formulieren

$\mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}$

Dies ist das zugrundeliegende Modell in der Grundgesamtheit und wird auch als „wahres Modell“ bezeichnet. Hierbei stehen $\mathbf y$ , ${\boldsymbol {\varepsilon }}$ und ${\boldsymbol {\beta }}$ für die Vektoren bzw. Matrizen:

$\mathbf {y} ={\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{t}\\\vdots \\y_{T}\end{pmatrix}}_{(T\times 1)}\;,\;\;\;\;\;$ ${\boldsymbol {\varepsilon }}={\begin{pmatrix}\varepsilon _{1}\\\varepsilon _{2}\\\vdots \\\varepsilon _{t}\\\vdots \\\varepsilon _{T}\end{pmatrix}}_{(T\times 1)}\;\;\;\;$ und $\;\;\;{\boldsymbol {\beta }}={\begin{pmatrix}\beta _{1}\\\beta _{2}\\\vdots \\\beta _{k}\\\vdots \\\beta _{K}\end{pmatrix}}_{(K\times 1)}$

und $\mathbf {X}$ eine $T\times K$ -Matrix (Versuchsplan- oder Datenmatrix):

$\mathbf {X} ={\begin{pmatrix}x_{11}&x_{12}&\cdots &x_{1k}&\cdots &x_{1K}\\x_{21}&x_{22}&\cdots &x_{2k}&\cdots &x_{2K}\\\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\x_{t1}&x_{t2}&\cdots &x_{tk}&\cdots &x_{tK}\\\vdots &\vdots &\ddots &\vdots &\ddots &\vdots \\x_{T1}&x_{T2}&\cdots &x_{Tk}&\cdots &x_{TK}\end{pmatrix}}_{(T\times K)}={\begin{pmatrix}\ \mathbf {x} _{1}^{\top }\\\ \mathbf {x} _{2}^{\top }\\\vdots \\\ \mathbf {x} _{t}^{\top }\\\vdots \\\\\mathbf {x} _{T}^{\top }\end{pmatrix}}_{(T\times K)}={\begin{pmatrix}\mathbf {x} _{(1)}\mathbf {x} _{(2)}&\cdots &\mathbf {x} _{(k)}&\cdots &\mathbf {x} _{(K)}\end{pmatrix}}_{(T\times K)}\quad$ , wobei $\quad \mathbf {x} _{(1)}\equiv 1\!\!1_{T}={\begin{pmatrix}1\\1\\\vdots \\1\\\vdots \\1\end{pmatrix}}_{(T\times 1)}$

Aufgrund der unterschiedlichen Schreibweisen für ${\mathbf {X}}$ lässt sich erkennen, dass sich das Modell $\mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}$ auch darstellen lässt als:

$y_{t}=x_{t1}\beta _{1}+x_{t2}\beta _{2}+\dotsb +x_{tK}\beta _{K}+\varepsilon _{t}=\mathbf {x} _{t}^{\top }{\boldsymbol {\beta }}+\varepsilon _{t},\quad t=1,2,\dotsc ,T$

mit

$\mathbf {x} _{t}={\begin{pmatrix}\ x_{t1}\\\ x_{t2}\\\vdots \\\ x_{tk}\\\vdots \\\\x_{tK}\end{pmatrix}}_{(K\times 1)}$ ,

hierbei ist y_t die beobachtete abhängige Variable für Beobachtung und $x_{tk}\;,t=1,\ldots ,T$ , sind die unabhängigen Variablen. Wie gewöhnlich ist, $\beta _{1}$ das Absolutglied und $\beta _{2},\beta _{3},\dotsc ,\beta _{K}$ sind unbekannte skalare Steigungsparameter. Die Störgröße $\varepsilon _{t}$ für Beobachtung ist eine unbeobachtbare Zufallsvariable. Der Vektor $\mathbf {x} _{t}^{\top }$ ist der transponierte Vektor der Regressoren und $\mathbf {x} _{t}^{\top }{\boldsymbol {\beta }}$ wird auch als linearer Prädiktor bezeichnet.

Die wesentliche Voraussetzung an das multiple lineare Regressionsmodell ist, dass es bis auf die Störgröße ${\boldsymbol {\varepsilon }}$ das „wahre Modell“ beschreibt. Dabei wird in der Regel nicht genau spezifiziert, von welcher Art die Störgröße ist; sie kann beispielsweise von zusätzlichen Faktoren oder Messfehlern herrühren. Jedoch nimmt man als Grundvoraussetzung an, dass dessen Erwartungswert (in allen Komponenten) 0 ist: $\operatorname {E} ({\boldsymbol {\varepsilon }})={\boldsymbol {0}}$ (Annahme 1). Diese Annahme bedeutet, dass das Modell grundsätzlich für korrekt gehalten wird und die beobachtete Abweichung als zufällig angesehen wird oder von vernachlässigbaren äußeren Einflüssen herrührt. Typisch ist die Annahme, dass die Komponenten des Vektors unkorreliert sind (Annahme 2) und dieselbe Varianz $\sigma ^{2}$ besitzen (Annahme 3), wodurch sich mit Hilfe klassischer Verfahren wie der Methode der kleinsten Quadrate (englisch ordinary least squares, kurz: OLS) einfache Schätzer für die unbekannten Parameter ${\boldsymbol {\beta }}$ und $\sigma ^{2}$ ergeben. Die Methode wird daher auch (multiple lineare) KQ-Regression (englisch OLS regression) genannt.

Zusammenfassend wird für die Störgrößen angenommen, dass

(A1) sie den Erwartungswert null haben: $\operatorname {E} ({\boldsymbol {\varepsilon }})=\mathbf {0} \$ ,
(A2) unkorreliert sind: $\operatorname {Cov} (\varepsilon _{t},\varepsilon _{s})=\operatorname {E} [(\varepsilon _{t}-\operatorname {E} (\varepsilon _{t}))((\varepsilon _{s}-\operatorname {E} (\varepsilon _{s}))]=\operatorname {E} (\varepsilon _{t}\varepsilon _{s})=0\quad \forall t\neq s$ und
(A3) eine homogene Varianz haben: ${\mbox{Cov}}({\boldsymbol {\varepsilon }})=\sigma ^{2}\mathbf {I} _{T}$ (skalare Kovarianzmatrix).

Hierbei bezeichnet $\mathbf {0}$ den Nullvektor und $\mathbf {I} _{T}$ die Einheitsmatrix der Dimension . Die oben genannten Annahmen sind die Annahmen der klassischen linearen Regression. Das Modell (die Gleichung $\mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}$ zusammen mit obigen Annahmen) wird daher das klassische Modell der linearen Mehrfachregression genannt.

Statt nur die Varianzen und Kovarianzen der Störgrößen einzeln zu betrachten, werden diese in folgender Kovarianzmatrix zusammengefasst:

${\begin{aligned}{\mbox{Cov}}({\boldsymbol {\varepsilon }})&=\operatorname {E} \left(({\boldsymbol {\varepsilon }}-\underbrace {\operatorname {E} ({\boldsymbol {\varepsilon }})} _{=\mathbf {0} \;{\text{aus A1}}})({\boldsymbol {\varepsilon }}-\underbrace {\operatorname {E} ({\boldsymbol {\varepsilon }})} _{=\mathbf {0} \;{\text{aus A1}}})^{\top }\right)=\operatorname {E} ({\boldsymbol {\varepsilon }}{\boldsymbol {\varepsilon }}^{\top })={\begin{pmatrix}\operatorname {Var} (\varepsilon _{1})&\operatorname {Cov} (\varepsilon _{1},\varepsilon _{2})&\cdots &\operatorname {Cov} (\varepsilon _{1},\varepsilon _{T})\\\\\operatorname {Cov} (\varepsilon _{2},\varepsilon _{1})&\operatorname {Var} (\varepsilon _{2})&\cdots &\operatorname {Cov} (\varepsilon _{2},\varepsilon _{T})\\\\\vdots &\vdots &\ddots &\vdots \\\\\operatorname {Cov} (\varepsilon _{T},\varepsilon _{1})&\operatorname {Cov} (\varepsilon _{T},\varepsilon _{2})&\cdots &\operatorname {Var} (\varepsilon _{T})\end{pmatrix}}\\&{\stackrel {\text{aus A2}}{=}}{\begin{pmatrix}\sigma ^{2}&0&\cdots &0\\0&\sigma ^{2}&\ddots &\vdots \\\vdots &\ddots &\ddots &0\\0&\cdots &0&\sigma ^{2}\end{pmatrix}}_{(T\times T)}=\sigma ^{2}\mathbf {I} _{T}\end{aligned}}$

Somit gilt für $\mathbf{y}$

$\operatorname {E} (\mathbf {y} )=\mathbf {X} {\boldsymbol {\beta }}\quad$ mit $\quad {\mbox{Cov}}(\mathbf {y} )={\mbox{Cov}}({\boldsymbol {\varepsilon }})=\sigma ^{2}\mathbf {I} _{T}$ .

Über diese grundlegende Annahme hinaus sind grundsätzlich alle Verteilungsannahmen an ${\boldsymbol {\varepsilon }}$ erlaubt. Wird zudem vorausgesetzt, dass der Vektor ${\boldsymbol {\varepsilon }}$ mehrdimensional normalverteilt ist, lässt sich ferner zeigen, dass die beiden Schätzer Lösungen der Maximum-Likelihood-Gleichungen sind (siehe Statistische Inferenz). In diesem Modell ist die Unabhängigkeit der Störgrößen dann gleichbedeutend mit der der y_t .

Schätzung des Parametervektors mit der Kleinste-Quadrate-Schätzung

Auch im multiplen linearen Regressionsmodell wird der Vektor der Störgrößen mithilfe der Kleinste-Quadrate-Schätzung (KQ-Schätzung) minimiert, das heißt, es soll ${\boldsymbol {\beta }}$ so gewählt werden, dass die euklidische Norm $\|\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}\|_{2}$ minimal wird. Im Folgenden wird der Ansatz benutzt, dass die Residuenquadratsumme minimiert wird. Dazu wird vorausgesetzt, dass $\mathbf {X}$ den Rang hat. Dann ist $\mathbf {X} ^{\top }\mathbf {X}$ invertierbar und man erhält als Minimierungsproblem:

${\underset {\boldsymbol {\beta }}{\rm {arg\,min}}}\,Q({\boldsymbol {\beta }})={\underset {\boldsymbol {\beta }}{\rm {arg\,min}}}\,(\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }})^{\top }(\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }})={\underset {\boldsymbol {\beta }}{\rm {arg\,min}}}\,\sum _{t=1}^{T}(y_{t}-\mathbf {x} _{t}^{\top }{\boldsymbol {\beta }})^{2}={\underset {\boldsymbol {\beta }}{\rm {arg\,min}}}\,\left(\mathbf {y} ^{\top }\mathbf {y} -2{\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {y} +{\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {X} {\boldsymbol {\beta }}\right)$

Die Bedingung erster Ordnung (Nullsetzen des Gradienten) lautet:

${\frac {\partial \,Q({\boldsymbol {\beta }})}{\partial {\boldsymbol {\beta }}}}={\begin{pmatrix}{\frac {\partial \,Q({\boldsymbol {\beta }})}{\partial \beta _{1}}}\\{\frac {\partial \,Q({\boldsymbol {\beta }})}{\partial \beta _{2}}}\\\vdots \\{\frac {\partial \,Q({\boldsymbol {\beta }})}{\partial \beta _{K}}}\end{pmatrix}}{\overset {\mathrm {!} }{=}}\;\mathbf {0}$

Die Kleinste-Quadrate-Schätzung kann als eine Projektion auf die Ebene, die durch die Regressoren aufgespannt wird, interpretiert werden.

Die partiellen Ableitungen erster Ordnung lauten:

${\begin{aligned}{\frac {\partial \,Q({\boldsymbol {\beta }})}{\partial \beta _{1}}}&={\frac {\partial (\mathbf {y} ^{\top }\mathbf {y} )}{\partial \beta _{1}}}-{\frac {\partial (2{\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {y} )}{\partial \beta _{1}}}+{\frac {\partial ({\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {X} {\boldsymbol {\beta }})}{\partial \beta _{1}}}=-2\mathbf {x} _{(1)}^{\top }\mathbf {y} +2\mathbf {x} _{(1)}^{\top }\mathbf {X} {\boldsymbol {\beta }}\\{\frac {\partial \,Q({\boldsymbol {\beta }})}{\partial \beta _{2}}}&={\frac {\partial (\mathbf {y} ^{\top }\mathbf {y} )}{\partial \beta _{2}}}-{\frac {\partial (2{\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {y} )}{\partial \beta _{2}}}+{\frac {\partial ({\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {X} {\boldsymbol {\beta }})}{\partial \beta _{2}}}=-2\mathbf {x} _{(2)}^{\top }\mathbf {y} +2\mathbf {x} _{(2)}^{\top }\mathbf {X} {\boldsymbol {\beta }}\\\vdots \\{\frac {\partial \,Q({\boldsymbol {\beta }})}{\partial \beta _{K}}}&={\frac {\partial (\mathbf {y} ^{\top }\mathbf {y} )}{\partial \beta _{K}}}-{\frac {\partial (2{\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {y} )}{\partial \beta _{K}}}+{\frac {\partial ({\boldsymbol {\beta }}^{\top }\mathbf {X} ^{\top }\mathbf {X} {\boldsymbol {\beta }})}{\partial \beta _{K}}}=-2\mathbf {x} _{(K)}^{\top }\mathbf {y} +2\mathbf {x} _{(K)}^{\top }\mathbf {X} {\boldsymbol {\beta }}\end{aligned}}$

Dies zeigt, dass sich die Bedingung erster Ordnung für den Vektor $\mathbf{b}$ der geschätzten Regressionsparameter kompakt darstellen lässt als:

$\left.{\frac {\partial Q({\boldsymbol {\beta }})}{\partial \mathbf {\beta } }}\right|_{\mathbf {b} }=-2\mathbf {X} ^{\top }\mathbf {y} +2\mathbf {X} ^{\top }\mathbf {X} \mathbf {b} \;{\overset {\mathrm {!} }{=}}\;\mathbf {0}$

bzw.

$\mathbf {X} ^{\top }\mathbf {X} \mathbf {b} =\mathbf {X} ^{\top }\mathbf {y}$ .

Dieses lineare Gleichungssystem wird in der Regel (Gaußsches) Normalgleichungssystem genannt.

Da die Matrix ${\mathbf {X}}$ den Rang hat, ist die quadratische symmetrische Matrix $\mathbf {X} ^{\top }\mathbf {X}$ nichtsingulär und die Inverse für $\mathbf {X} ^{\top }\mathbf {X}$ existiert. Daher erhält man nach linksseitiger Multiplikation mit der Inversen der Produktsummenmatrix $(\mathbf {X} ^{\top }\mathbf {X} )^{-1}$ als Lösung des Minimierungsproblems den folgenden Vektor der geschätzten Regressionskoeffizienten:

$\mathbf {b} ={\begin{pmatrix}b_{1}\\b_{2}\\b_{2}\\\vdots \\b_{K}\end{pmatrix}}=(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y}$

Wenn der Rang von ${\mathbf {X}}$ kleiner als ist, dann ist $\mathbf {X} ^{\top }\mathbf {X}$ nicht invertierbar, also das Normalgleichungssystem nicht eindeutig lösbar, mithin $\mathbf{b}$ nicht identifizierbar, siehe hierzu aber den Begriff der Schätzbarkeit. Da $\mathbf{b}$ die Residuenquadratsumme minimiert, wird $\mathbf{b}$ auch Kleinste-Quadrate-Schätzer (kurz: KQ-Schätzer) genannt. Alternativ kann der Kleinste-Quadrate-Schätzer durch Einsetzen des wahren Modells $\mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}$ auch dargestellt werden als

$\mathbf {b} =(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }(\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }})={\boldsymbol {\beta }}+(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}$

Für die Kovarianzmatrix des Kleinste-Quadrate-Schätzers ergibt sich (dargestellt in kompakter Form):^[5]

$\operatorname {Cov} (\mathbf {b} )={\boldsymbol {\beta }}+(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}=(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\operatorname {Cov} (\mathbf {Y} )\ \mathbf {X} (\mathbf {X} ^{\top }\mathbf {X} )^{-1}=\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )^{-1}=\Sigma _{\mathbf {b} }$

Im Fall der linearen Einfachregression ( ${\boldsymbol {\beta }}=(\beta _{1},\beta _{2})^{\top }$ ) reduziert sich die obigen Formel auf die bekannten Ausdrücke für die Varianzen der KQ-Schätzer $\operatorname {Var} (\beta _{2})={\frac {\sigma ^{2}}{\sum _{t=1}^{T}(x_{t2}-{\overline {x}}_{2})^{2}}}$ und $\operatorname {Var} (\beta _{1})={\frac {\sigma ^{2}\sum _{t=1}^{T}x_{t2}^{2}}{T\sum _{t=1}^{T}(x_{t2}-{\overline {x}}_{2})^{2}}}$ (siehe Statistische Eigenschaften der Kleinste-Quadrate-Schätzer).

Beweis

${\begin{aligned}\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )^{-1}&=\sigma ^{2}\left({\begin{pmatrix}1&1&\cdots \\x_{12}&x_{22}&\cdots \end{pmatrix}}{\begin{pmatrix}1&x_{12}\\1&x_{22}\\\vdots &\vdots \,\,\,\end{pmatrix}}\right)^{-1}\\[6pt]&=\sigma ^{2}\left(\sum _{t=1}^{T}{\begin{pmatrix}1&x_{t2}\\x_{t2}&x_{t2}^{2}\end{pmatrix}}\right)^{-1}\\[6pt]&=\sigma ^{2}{\begin{pmatrix}T&\sum x_{t2}\\\sum x_{t2}&\sum x_{t2}^{2}\end{pmatrix}}^{-1}\\[6pt]&=\sigma ^{2}\cdot {\frac {1}{T\sum x_{t2}^{2}-(\sum x_{i2})^{2}}}{\begin{pmatrix}\sum x_{t2}^{2}&-\sum x_{t2}\\-\sum x_{t2}&T\end{pmatrix}}\\[6pt]&=\sigma ^{2}\cdot {\frac {1}{T\sum {(x_{t2}-{\overline {x}})^{2}}}}{\begin{pmatrix}\sum x_{t2}^{2}&-\sum x_{t2}\\-\sum x_{t2}&T\end{pmatrix}}\\[8pt]\Rightarrow \operatorname {Var} (\beta _{1})&=\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )_{11}^{-1}={\frac {\sigma ^{2}\sum _{t=1}^{T}x_{t2}^{2}}{T\sum _{t=1}^{T}(x_{t2}-{\overline {x}}_{2})^{2}}}\\\Rightarrow \operatorname {Var} (\beta _{2})&=\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )_{22}^{-1}={\frac {\sigma ^{2}}{\sum _{t=1}^{T}(x_{t2}-{\overline {x}}_{2})^{2}}}.\end{aligned}}$

Man erhält mit Hilfe des Kleinste-Quadrate-Schätzers $\mathbf{b}$ das Gleichungssystem

${\hat {\mathbf {y} }}=\mathbf {X} \mathbf {b} =\mathbf {y} -{\hat {\boldsymbol {\varepsilon }}}$ ,

wobei ${\hat {\boldsymbol {\varepsilon }}}$ der Vektor der Residuen und ${\hat {\mathbf {y} }}$ die Schätzung für $\mathbf{y}$ ist. Das Interesse der Analyse liegt oft in der Schätzung ${\hat {\mathbf {y} }}_{0}$ oder in der Vorhersage der abhängigen Variablen $\mathbf{y}$ für ein gegebenes Tupel von ${\mathbf {x} }_{0}$ . Diese berechnet sich als

${\hat {\mathbf {y} }}_{0}=x_{01}b_{1}+x_{02}b_{2}+\dotsc +x_{0K}b_{K}=\mathbf {x} _{0}^{\top }{\mathbf {b} }$ .

Güteeigenschaften des Kleinste-Quadrate-Schätzers

Erwartungstreue

Im multiplen Fall kann man genauso wie im einfachen Fall zeigen, dass der Kleinste-Quadrate-Schätzvektor erwartungstreu für ${\boldsymbol {\beta }}$ ist. Dies gilt allerdings nur, wenn die Annahme der Exogenität der Regressoren gegeben ist. Dies ist der Fall, wenn die möglicherweise zufälligen Regressoren und die Störgrößen unkorreliert sind, d.h. wenn $\operatorname {E} (\mathbf {x} ^{\top }\mathbf {\cdot } {\boldsymbol {\varepsilon }})\mathbf {=} 0$ gilt. Wenn man also hier voraussetzt, dass die exogenen Variablen keine Zufallsvariablen sind, sondern wie in einem Experiment kontrolliert werden können, gilt $\forall k\in \{1,\dotsc ,K\}\colon \operatorname {E} (x_{tk}\varepsilon _{t})=x_{tk}\cdot \operatorname {E} (\varepsilon _{t})=0$ bzw. $\operatorname {E} (\mathbf {x} ^{\top }\mathbf {\cdot } {\boldsymbol {\varepsilon }})=\mathbf {0}$ und damit ist ${\mathbf b}$ erwartungstreu für ${\boldsymbol {\beta }}$ .

Beweis

${\begin{aligned}\operatorname {E} (\mathbf {b} )&=\operatorname {E} ((\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} )\\&=\operatorname {E} ((\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }(\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}))\\&=\operatorname {E} ((\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {X} {\boldsymbol {\beta }}+(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}))=(\mathbf {X} ^{\top }\mathbf {X} )^{-1}(\mathbf {X} ^{\top }\mathbf {X} ){\boldsymbol {\beta }}+(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\underbrace {\operatorname {E} (\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }})} _{=\mathbf {0} }={\boldsymbol {\beta }}\end{aligned}}$

Falls die Exogenitätsannahme nicht zutrifft, $\operatorname {E} (\mathbf {x} ^{\top }{\boldsymbol {\varepsilon }})\mathbf {\neq } 0$ , ist der Kleinste-Quadrate-Schätzer nicht erwartungstreu. Es liegt also eine Verzerrung (englisch bias) vor, d.h., „im Mittel“ weicht der Parameterschätzer vom wahren Parameter ab:

$\operatorname {Bias} \left(\mathbf {b} \right)=\operatorname {E} (\mathbf {b} )-{\boldsymbol {\beta }}\neq \mathbf {0}$ .

Der Erwartungswert des Kleinste-Quadrate-Parametervektor für ${\mathbf b}$ ist also nicht gleich dem wahren Parameter ${\boldsymbol {\beta }}$ , siehe dazu auch unter Regression mit stochastischen Regressoren.

Effizienz

Der Kleinste-Quadrate-Schätzer ist linear:

$\mathbf {b} =\underbrace {(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }} _{:=\mathbf {A} }\mathbf {y} =\mathbf {A} \mathbf {y}$ .

Nach dem Satz von Gauß-Markow ist der Schätzer $\mathbf{b}$ , bester linearer erwartungstreuer Schätzer (BLES bzw. englisch Best Linear Unbiased Estimator, kurz: BLUE), das heißt, er ist derjenige lineare erwartungstreue Schätzer, der unter allen linearen erwartungstreuen Schätzern die kleinste Varianz bzw. Kovarianzmatrix besitzt. Für diese Eigenschaften der Schätzfunktion $\mathbf{b}$ braucht keine Verteilungsinformation der Störgröße vorzuliegen. Wenn die Störgrößen normalverteilt sind, ist $\mathbf{b}$ Maximum-Likelihood-Schätzer und nach dem Satz von Lehmann-Scheffé beste erwartungstreue Schätzung (BES bzw. englisch Best Unbiased Estimator, kurz: BUE).

Konsistenz

Der KQ-Schätzer ist unter den bisherigen Annahmen erwartungstreu für ${\boldsymbol {\beta }}$ ( $\operatorname {E} (\mathbf {b} )={\boldsymbol {\beta }}$ ), wobei die Stichprobengröße keinen Einfluss auf die Erwartungstreue hat (schwaches Gesetz der großen Zahlen). Ein Schätzer ist genau dann konsistent für den wahren Wert, wenn er in Wahrscheinlichkeit gegen den wahren Wert konvergiert (englisch probability limit, kurz: plim). Die Eigenschaft der Konsistenz bezieht also das Verhalten des Schätzers mit ein, wenn die Anzahl der Beobachtungen größer wird.

Für die Folge $(\mathbf {b} _{t})_{t\in \mathbb {N} }$ gilt, dass sie in Wahrscheinlichkeit gegen den wahren Parameterwert ${\boldsymbol {\beta }}$ konvergiert

$\forall \epsilon >0\colon \lim _{t\to \infty }\mathbb {P} (|\mathbf {b} _{t}-{\boldsymbol {\beta }}|\geq \epsilon )=0$

oder vereinfacht ausgedrückt $\quad \mathbf {b} \;{\stackrel {p}{\longrightarrow }}\;\mathbf {\boldsymbol {\beta }} \quad$ bzw. $\quad \operatorname {plim} (\mathbf {b} )={\boldsymbol {\beta }}$

Die Grundlegende Annahme, um die Konsistenz des KQ-Schätzers sicherzustellen lautet

$\lim _{T\to \infty }\left({\frac {\mathbf {X} _{T}^{\top }\mathbf {X} _{T}}{T}}\right)=\mathbf {Q}$ ,

d.h. man geht davon aus, dass das durchschnittliche Quadrat der beobachteten Werte der erklärenden Variablen auch bei einem ins Unendliche gehendem Stichprobenumfang endlich bleibt (siehe Produktsummenmatrix). Außerdem nimmt man an, dass

$\operatorname {plim} \left({\frac {\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}}{T}}\right)=0$ .

Die Konsistenz kann wie folgt gezeigt werden:

Beweis

${\begin{aligned}\operatorname {plim} (\mathbf {b} )&=\operatorname {plim} ((\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y} )\\&=\operatorname {plim} ({\boldsymbol {\beta }}+(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}))\\&={\boldsymbol {\beta }}+\operatorname {plim} ((\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }})\\&={\boldsymbol {\beta }}+\operatorname {plim} \left(((\mathbf {X} ^{\top }\mathbf {X} )^{-1}/T)\right)\cdot \operatorname {plim} \left(((\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }})/T)\right)\\&={\boldsymbol {\beta }}+[\operatorname {plim} \left(((\mathbf {X} ^{\top }\mathbf {X} )/T)\right)]^{-1}\cdot \underbrace {\operatorname {plim} \left(((\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }})/T)\right)} _{=0}={\boldsymbol {\beta }}+\mathbf {Q} ^{-1}\cdot 0={\boldsymbol {\beta }}\end{aligned}}$

Hierbei wurde das Slutsky-Theorem und die Eigenschaft verwendet, dass wenn ${\mathbf {X}}$ deterministisch bzw. nichtstochastisch ist $\operatorname {plim} \left((\mathbf {X} ^{\top }\mathbf {X} )/T\right)=\lim \left((\mathbf {X} ^{\top }\mathbf {X} )/T\right)$ gilt.

Folglich ist der Kleinste-Quadrate-Schätzer konsistent für ${\boldsymbol {\beta }}$ . Die Eigenschaft besagt, dass mit steigender Stichprobengröße die Wahrscheinlichkeit, dass der Schätzer ${\mathbf b}$ vom wahren Parameter ${\boldsymbol {\beta }}$ abweicht, sinkt. Weiterhin lässt sich durch das Chintschin-Theorem zeigen, dass für die durch die KQ-Schätzung gewonnene Störgrößenvarianz gilt, dass sie konsistent für $\sigma ^{2}$ ist, d. h. $\operatorname {plim} ({\hat {\sigma }}^{2})=\sigma ^{2}$ .

Beweis

Dazu schreibt man zunächst die geschätzte Störgrößenvarianz wie folgt um

${\begin{aligned}{\hat {\sigma }}^{2}&={\frac {\left(\mathbf {y} -\mathbf {X} \mathbf {b} \right)^{\top }\left(\mathbf {y} -\mathbf {X} \mathbf {b} \right)}{T-K}}\\&={\frac {1}{T-K}}{\boldsymbol {\varepsilon }}^{\top }\left(\mathbf {I} -\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\right){\boldsymbol {\varepsilon }}\\&=\left({\frac {T}{T-K}}\right)\left({\frac {{\boldsymbol {\varepsilon }}^{\top }{\boldsymbol {\varepsilon }}}{T}}-{\frac {{\boldsymbol {\varepsilon }}^{\top }\mathbf {X} }{T}}\left({\frac {\mathbf {X} ^{\top }\mathbf {X} }{T}}\right)^{-1}{\frac {\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}}{T}}\right)\end{aligned}}$

Damit ergibt sich als Wahrscheinlichkeitslimes

$\operatorname {plim} ({\hat {\sigma }}^{2})=\operatorname {plim} \left(\left({\frac {T}{T-K}}\right)\left({\frac {{\boldsymbol {\varepsilon }}^{\top }{\boldsymbol {\varepsilon }}}{T}}-{\frac {{\boldsymbol {\varepsilon }}^{\top }\mathbf {X} }{T}}\left({\frac {\mathbf {X} ^{\top }\mathbf {X} }{T}}\right)^{-1}{\frac {\mathbf {X} ^{\top }{\boldsymbol {\varepsilon }}}{T}}\right)\right)=\sigma ^{2}-0\cdot \mathbf {Q} ^{-1}\cdot 0=\sigma ^{2}$

Somit ist ${\hat \sigma }^{2}$ ein konsistenter Schätzer für $\sigma ^{2}$ .

Verbindung zur optimalen Versuchsplanung

Wenn die Werte der unabhängigen Variablen $\mathbf {x} _{k}$ einstellbar sind, kann durch optimale Wahl dieser Werte die Matrix $(\mathbf {X} ^{\top }\mathbf {X} )^{-1}$ (d.h. bis auf einen Faktor die Kovarianzmatrix des Kleinste-Quadrate-Schätzers) im Sinne der Loewner-Halbordnung „verkleinert“ werden. Das ist eine Hauptaufgabe der optimalen Versuchsplanung.

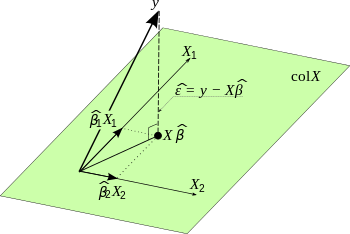
Residuen und geschätzte Zielwerte

Die Schätzwerte der y_t berechnen sich mithilfe des KQ-Schätzers $\mathbf {b}$ als

${\hat {\mathbf {y} }}=\mathbf {Xb} =\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\mathbf {y}$ ,

wobei man dies auch kürzer als

${\hat {\mathbf {y} }}=\mathbf {P} \mathbf {y}$ mit $\mathbf {P} \in \mathbb {R} ^{T\times T}$

schreiben kann. Die Projektionsmatrix $\mathbf{P}$ ist die Matrix der Orthogonalprojektion auf den Spaltenraum von $\mathbf {X}$ und hat maximal den Rang . Sie wird auch Prädiktionsmatrix genannt, da sie die vorhergesagten Werte ( ${\hat {y}}$ -Werte) generiert wenn man die Matrix auf die -Werte anwendet. Die Prädiktionsmatrix beschreibt numerisch die Projektion von auf die durch ${\mathbf {X}}$ definierte Ebene.

Der Residualvektor lässt sich mittels der Prädiktionsmatrix darstellen als: ${\hat {\boldsymbol {\varepsilon }}}=\mathbf {y} -{\hat {\mathbf {y} }}=\mathbf {y} -\mathbf {X} \mathbf {b} =(\mathbf {I} -\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top })\mathbf {y} =(\mathbf {I} -\mathbf {P} )\mathbf {y}$ .

Die Matrix $(\mathbf {I} -\mathbf {X} \left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top })=\left(\mathbf {I} -\mathbf {P} \right)$ wird auch als Residualmatrix bezeichnet und mit $\mathbf M$ abgekürzt. Ferner ist die Residuenquadratsumme als nichtlineare Transformation Chi-Quadrat-verteilt mit $(T-K)$ Freiheitsgraden. Dies zeigt folgende Beweisskizze:

Beweisskizze

Sei

${\boldsymbol {\varepsilon }}=\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}$ ,

damit erhält man

${\begin{aligned}{\boldsymbol {\varepsilon }}^{\top }\left(\mathbf {I} -\mathbf {P} \right){\boldsymbol {\varepsilon }}/\sigma ^{2}&=(\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }})^{\top }\mathbf {M} \mathbf {M} (\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }})/\sigma ^{2}\\&=\mathbf {y} ^{\top }\mathbf {M} \mathbf {y} /\sigma ^{2}\\&=SQR/\sigma ^{2}\sim \chi ^{2}(T-K)\end{aligned}}$ ,

wobei

$\mathbf {M} \mathbf {X} =0$

und der Satz von Cochran verwendet wurden.

Außerdem gilt ebenso

$\|{\hat {\mathbf {y} }}-\mathbf {X} {\boldsymbol {\beta }}\|_{2}^{2}/\sigma ^{2}\sim \chi _{K}^{2}$ .

Erwartungstreue Schätzung des unbekannten Varianzparameters

→ Hauptartikel: Erwartungstreue Schätzung der Varianz der Störgrößen

Obwohl manchmal angenommen wird, dass die Störgrößenvarianz $\sigma ^{2}$ bekannt ist, muss man davon ausgehen, dass sie in den meisten Anwendungsfällen unbekannt ist (beispielsweise bei der Schätzung von Nachfrageparametern in ökonomischen Modellen, oder Produktionsfunktionen). Ein naheliegender Schätzer des Vektors der Störgrößen $\boldsymbol{\varepsilon}$ ist der Residulavektor ${\hat {\boldsymbol {\varepsilon }}}=\left(\mathbf {y} -\mathbf {X} \mathbf {b} \right)$ , der aus der Regression gewonnen wird. Die in den Residuen steckende Information könnte also für einen Schätzer der Störgrößenvarianz genutzt werden. Aufgrund der Tatsache, dass $\operatorname {E} (\varepsilon _{t}^{2})=\sigma ^{2}$ gilt, ist $\sigma ^{2}$ aus frequentistischer Sicht der „Mittelwert“ von $\varepsilon _{t}^{2}$ . Die Größe $\varepsilon _{t}^{2}$ ist aber unbeobachtbar, da die Störgrößen unbeobachtbar sind. Wenn man statt $\varepsilon _{t}^{2}$ nun das beobachtbare Pendant ${\hat {\varepsilon }}_{t}^{2}$ benutzt, führt dies zum Schätzer:

${\tilde {s}}^{2}={\frac {1}{T}}\sum \nolimits _{t=1}^{T}{\hat {\varepsilon }}_{t}^{2}={\frac {1}{T}}{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}={\frac {1}{T}}SQR$ ,

wobei $SQR$ die Residuenquadratsumme darstellt. Allerdings erfüllt der Schätzer nicht gängige Qualitätskriterien für Punktschätzer und wird daher nicht oft genutzt. Beispielsweise ist der Schätzer nicht erwartungstreu für $\sigma ^{2}$ . Dies liegt daran, dass der Erwartungswert der Residuenquadratsumme $\operatorname {E} ({\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}})=\sigma ^{2}(T-K)$ ergibt und daher für den Erwartungswert dieses Schätzers $\operatorname {E} ({\hat {\sigma }}_{\text{ML}}^{2})={\frac {T-K}{T}}\sigma ^{2}$ gilt. Eine erwartungstreue Schätzung für $\sigma ^{2}$ , d.h. eine Schätzung die $\operatorname {E} ({\hat {\sigma }}^{2})=\sigma ^{2}$ erfüllt, ist in der multiplen linearen Regression gegeben ist durch das mittlere Residuenquadrat

${\hat {\sigma }}^{2}=SQR/(T-K)={\frac {{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}}{T-K}}={\frac {\left(\mathbf {y} -\mathbf {X} \mathbf {b} \right)^{\top }\left(\mathbf {y} -\mathbf {X} \mathbf {b} \right)}{T-K}}$ mit dem Kleinste-Quadrate-Schätzer $\mathbf {b} =(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} ^{\top }\mathbf {y}$ .

Wenn nun bei der Kovarianzmatrix des KQ-Schätzvektors $\sigma ^{2}$ durch ${\hat {\sigma }}^{2}$ ersetzt wird ergibt sich für die geschätzte Kovarianzmatrix des KQ-Schätzers

${\hat {\Sigma }}_{\mathbf {b} }={\hat {\sigma }}^{2}\left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}={\frac {{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}}{T-K}}\left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}$ .

Statistische Inferenz

→ Hauptartikel: Klassisches lineares Modell der Normalregression

Für die statistische Inferenz (Schätzen und Testen) wird noch die Information über die Verteilung des Vektors der Störgrößen $\boldsymbol{\varepsilon}$ gefordert. Bedingt auf die Datenmatrix ${\mathbf {X}}$ sind die $\varepsilon _{t}$ unabhängig und identisch verteilt und folgen einer ${\mathcal {N}}(0,\sigma ^{2})$ -Verteilung. Äquivalent ist $\boldsymbol{\varepsilon}$ (bedingt auf ${\mathbf {X}}$ ) mehrdimensional normalverteilt mit dem Erwartungswert $\mathbf {0}$ und der Kovarianzmatrix $\sigma ^{2}\mathbf {I} _{T}$ , d.h.

${\boldsymbol {\varepsilon }}\sim {\mathcal {N}}(\mathbf {0} ,\sigma ^{2}\mathbf {I} _{T})$

Hier sind stochastisch unabhängige Zufallsvariablen auch unkorreliert. Weil der Störgrößenvektor mehrdimensional normalverteilt ist folgt daraus, dass auch der Regressand mehrdimensional normalverteilt ist ( ${\boldsymbol {y}}\sim {\mathcal {N}}(\mathbf {X} {\boldsymbol {\beta }},\sigma ^{2}\mathbf {I} _{T})$ ). Aufgrund der Tatsache, dass beim KQ-Schätzer die einzige zufällige Komponente $\mathbf{y}$ ist, folgt für den Parametervektor $\mathbf{b}$ , dass er ebenfalls normalverteilt ist: $\mathbf {b} \sim {\mathcal {N}}({\boldsymbol {\beta }},\sigma ^{2}(\mathbf {X} ^{\top }\mathbf {X} )^{-1})$ .

Multiples Bestimmtheitsmaß

Das Bestimmtheitsmaß ${\mathit {R}}^{2}$ ist eine Maßzahl für die Güte (Bestimmtheit) einer multiplen linearen Regression. In der multiplen linearen Regression, lässt sich das Bestimmtheitsmaß darstellen als

${\mathit {R}}^{2}=1-{\frac {\mathbf {y} ^{\top }\mathbf {y} -\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {y} }{\mathbf {y} ^{\top }\mathbf {y} -T{\overline {y}}^{2}}}$ .

oder

${\mathit {R}}^{2}={\frac {SQE}{SQT}}={\frac {{\hat {\mathbf {y} }}^{\top }{\hat {\mathbf {y} }}-T{\overline {\hat {y}}}^{2}}{{\hat {\mathbf {y} }}^{\top }{\hat {\mathbf {y} }}+{\hat {\boldsymbol {\varepsilon }}}^{\top }{\hat {\boldsymbol {\varepsilon }}}-T{\overline {y}}^{2}}}={\frac {\mathbf {b} ^{\top }\mathbf {X} ^{\top }\mathbf {y} -T{\overline {y}}^{2}}{\mathbf {y} ^{\top }\mathbf {y} -T{\overline {y}}^{2}}}$ .

Die Besonderheit beim multiplen Bestimmtheitsmaß ist, dass es nicht wie in der einfachen linearen Regression dem quadrierten Korrelationskoeffizienten zwischen und , sondern dem Quadrat des Korrelationskoeffizienten zwischen den Messwerten y_t und den Schätzwerten ${\hat {y}}_{t}$ entspricht (für einen Beweis, siehe Matrixschreibweise).

Test auf Gesamtsignifikanz eines Modells

→ Hauptartikel: Globaler F-Test

Hat man eine Regression ermittelt, ist man auch an der Güte dieser Regression interessiert. Im Fall $x_{t1}=1$ für alle wird häufig als Maß für die Güte das Bestimmtheitsmaß $R^{2}$ verwendet. Generell gilt, je näher der Wert des Bestimmtheitsmaßes bei liegt, desto besser ist die Güte der Regression. Ist das Bestimmtheitsmaß klein, kann man seine Signifikanz durch das Hypothesenpaar

$H_{0}\colon \beta _{1}=\beta _{2}=\ldots =\beta _{k}\;=\;0\Rightarrow \rho ^{2}=0$ gegen $H_{1}:\beta _{j}\;\neq \;0\;\mathrm {f{\ddot {u}}r\;mindestens\;ein} \;j\in \{1,\ldots ,k\}\Rightarrow \rho ^{2}\neq 0$ ,

mit der Prüfgröße

$F={\frac {R^{2}/(K-1)}{(1-R^{2})/(T-K)}}\sim F(K-1,T-K)$

testen. Die Prüfgröße ist F-verteilt mit K-1 und $T-K$ Freiheitsgraden. Überschreitet die Prüfgröße bei einem Signifikanzniveau $\alpha$ den kritischen Wert $F(K-1,T-K)$ , das $(1-\alpha)$ -Quantil der F-Verteilung mit $(K-1)$ und $(T-K)$ Freiheitsgraden, wird $H_{0}$ abgelehnt. $R^{2}$ ist dann ausreichend groß, mindestens ein Regressor trägt also vermutlich genügend viel Information zur Erklärung von bei.

Unter den Voraussetzungen des klassischen linearen Regressionsmodells ist der Test ein Spezialfall der einfachen Varianzanalyse. Für jeden Beobachtungswert ist die Störgröße $\varepsilon _{t}\sim {\mathcal {N}}(0,\sigma ^{2})$ und damit $y_{t}\sim {\mathcal {N}}\left(\mu _{t}=x_{t1}\beta _{1}+x_{t2}\beta _{2}+\dotsc +x_{tK}\beta _{K},\sigma ^{2}\right)$ -verteilt (mit $\mu _{t}$ der wahre Regressionswert in der Grundgesamtheit), d.h., die Voraussetzungen der Varianzanalyse sind erfüllt. Sind alle $\beta _{k}$ -Koeffizienten gleich null, so ist dies äquivalent zur Nullhypothese der Varianzanalyse: $H_{0}\colon \mu _{1}=\dotsb =\mu _{T}$ .

Die Residualanalyse, bei der man die Residuen über den unabhängigen Variablen aufträgt, gibt Aufschluss über

die Richtigkeit des angenommenen linearen Zusammenhangs,
mögliche Ausreißer,
Homoskedastizität, Heteroskedastizität.

Ein Ziel bei der Residualanalyse ist es, die Voraussetzung der Residuen ${\hat {\varepsilon }}_{t}$ zu überprüfen. Hierbei ist es wichtig zu beachten, dass

${\hat {\varepsilon }}_{t}\neq \varepsilon _{t}$

gilt. Das Residuum ${\hat {\varepsilon }}_{t}$ ist mit der Formel ${\hat {\varepsilon }}_{t}=y_{t}-{\hat {y}}_{t}$ berechenbar. Im Gegensatz hierzu ist die Störgröße $\varepsilon _{t}$ nicht berechenbar oder beobachtbar. Nach den oben getroffenen Annahmen soll für alle Störgrößen gelten

$\operatorname {Var} (\varepsilon _{t})=\sigma ^{2}=\mathrm {konst.}$

Es liegt somit eine Varianzhomogenität vor. Dieses Phänomen wird auch als Homoskedastizität bezeichnet und ist auf die Residuen übertragbar. Dies bedeutet: Wenn man die unabhängigen Variablen gegen die Residuen ${\hat {\varepsilon }}$ aufträgt, sollten keine systematischen Muster erkennbar sein.

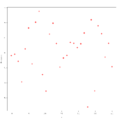Beispiel 1 zur Residualanalyse
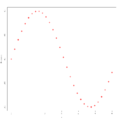Beispiel 2 zur Residualanalyse
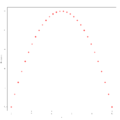Beispiel 3 zur Residualanalyse

In den obigen drei Grafiken wurden die unabhängigen Variablen gegen die Residuen ${\hat {\varepsilon }}$ abgetragen, und im Beispiel 1 sieht man, dass hier tatsächlich kein erkennbares Muster in den Residuen vorliegt, d.h., dass die Annahme der Varianzhomogenität erfüllt ist. In den Beispielen 2 und 3 dagegen ist diese Annahme nicht erfüllt: Man erkennt ein Muster. Zur Anwendung der linearen Regression sind daher hier zunächst geeignete Transformationen durchzuführen. So ist im Beispiel 2 ein Muster zu erkennen, das an eine Sinus-Funktion erinnert, womit hier eine Daten-Transformation der Form $a\cdot \sin(tx_{t}+c)$ denkbar wäre, während im Beispiel 3 ein Muster zu erkennen ist, das an eine Parabel erinnert, in diesem Fall also eine Daten-Transformation der Form $a\cdot (x_{t}-c)^{2}$ angebracht sein könnte.

Beitrag der einzelnen Regressoren zur Erklärung der abhängigen Variablen

Man ist daran interessiert, ob man einzelne Parameter oder Regressoren aus dem Regressionsmodell entfernen kann, ob also ein Regressor nicht (oder nur gering) zur Erklärung von $\mathbf y$ beiträgt. Dies ist dann möglich, falls ein Parameter $\beta _{k}$ gleich null ist, somit testet man die Nullhypothese $H_{0}\colon \beta _{k}=0$ . Das heißt, man testet, ob der -te Parameter gleich Null ist. Wenn dies der Fall ist, kann der zugehörige -te Regressor $x_{k}$ aus dem Modell entfernt werden. Der Vektor ${\mathbf b}$ ist als lineare Transformation von $\mathbf y$ wie folgt verteilt:

$\mathbf {b} \;\sim \;{\mathcal {N}}\left({\boldsymbol {\beta }},\sigma ^{2}{(\mathbf {X} ^{\top }\mathbf {X} )}^{-1}\right)$

Wenn man die Varianz der Störgrößen schätzt, erhält man für die geschätzte Kovarianzmatrix des Kleinste-Quadrate-Schätzers

${\hat {\Sigma }}_{\mathbf {b} }={\hat {\sigma }}^{2}(\mathbf {X} ^{\top }\mathbf {X} )^{-1}$ .

Die geschätzte Varianz $\sigma ^{2}$ eines Regressionsparameters b_k steht als -tes Diagonalelement in der geschätzten Kovarianzmatrix. Es ergibt sich die Prüfgröße

$t_{k}={\frac {b_{k}}{{\hat {\sigma }}_{b_{k}}}}\sim t(T-K)$ ,

wobei die Wurzel der geschätzten Varianz ${\hat {\sigma }}_{b_{k}}^{2}={\hat {\sigma }}^{2}(\mathbf {X} ^{\top }\mathbf {X} )_{kk}^{-1}$ des -ten Parameters den (geschätzten) Standardfehler des Regressionskoeffizienten ${\hat {\sigma }}_{b_{k}}$ darstellt.

Die Prüf- bzw. Pivotstatistik ist t-verteilt mit $T-K$ Freiheitsgraden. Ist $|t_{k}|$ größer als der kritische Wert $t_{(1-\alpha /2,T-K)}$ , dem $(1-\alpha /2)$ -Quantil der -Verteilung mit $T-K$ Freiheitsgraden, wird die Hypothese abgelehnt. Somit wird der Regressor $x_{k}$ im Modell beibehalten und der Beitrag des Regressors $x_{k}$ zur Erklärung von ist signifikant groß, d.h. signifikant von null verschieden.

Vorhersage

Ein einfaches Modell zur Vorhersage von endogenen Variablen ergibt sich durch

$\mathbf {y} _{0}=\mathbf {X} _{0}{\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}_{0}$ ,

wobei $\mathbf {y} _{0}$ den Vektor von zukünftigen abhängigen Variablen und $\mathbf {X} _{0}$ die Matrix der erklärenden Variablen zum Zeitpunkt $T_{0}$ darstellt.

Die Vorhersage wird wie folgt dargestellt: ${\hat {\mathbf {y} }}_{0}=\mathbf {X} _{0}\mathbf {b}$ , woraus sich folgender Vorhersagefehler ergibt: ${\hat {\mathbf {y} }}_{0}-\mathbf {y} _{0}$

Eigenschaften des Vorhersagefehlers:

Der Vorhersagefehler ist im Mittel null: $\operatorname {E} ({\hat {\mathbf {y} }}_{0}-\mathbf {y} _{0})=\operatorname {E} (\mathbf {X} _{0}(\mathbf {b} -{\boldsymbol {\beta }})-{\boldsymbol {\varepsilon }}_{0})=\mathbf {0}$

Die Kovarianzmatrix des Vorhersagefehlers lautet: $\operatorname {E} \left(({\hat {\mathbf {y} }}_{0}-\mathbf {y} _{0}-\operatorname {E} ({\hat {\mathbf {y} }}_{0}-\mathbf {y} _{0}))(({\hat {\mathbf {y} }}_{0}-\mathbf {y} _{0}-\operatorname {E} ({\hat {\mathbf {y} }}_{0}-\mathbf {y} _{0}))^{\top }\right)=\sigma ^{2}\left(\mathbf {X} _{0}(\mathbf {X} ^{\top }\mathbf {X} )^{-1}\mathbf {X} _{0}^{\top }+\mathbf {I} \right)$

Ermittelt man einen Vorhersagewert, möchte man möglicherweise wissen, in welchem Intervall sich die vorhergesagten Werte mit einer festgelegten Wahrscheinlichkeit bewegen. Man wird also ein Vorhersageintervall für den durchschnittlichen Vorhersagewert $\operatorname {E} (\mathbf {y} _{0})$ ermitteln. Im Fall der linearen Einfachregression ergibt sich für die Varianz des Vorhersagefehlers

$\operatorname {Var} ({\hat {y}}_{0}-y_{0})=\sigma ^{2}\left(1+{\frac {1}{T}}+{\frac {(x_{0}-{\overline {x}})^{2}}{\sum \limits _{t=1}^{\top }(x_{t}-{\overline {x}})^{2}}}\right)$ .

Man erhält dann als $(1-\alpha )$ Vorhersageintervall für die Varianz des Vorhersagefehlers

$\left[{\hat {y}}_{0}-t_{1-\alpha /2;T-K}\cdot {\sqrt {\operatorname {Var} ({\hat {y}}_{0}-y_{0})}}\;;\;{\hat {y}}_{0}+t_{1-\alpha /2;T-K}\cdot {\sqrt {\operatorname {Var} ({\hat {y}}_{0}-y_{0})}}\right]$ .

Speziell für den Fall der einfachen linearen Regression ergibt sich das Vorhersageintervall:

$\left[{\hat {y}}_{0}-t_{1-\alpha /2;T-K}\cdot {\sqrt {\sigma ^{2}\left(1+{\frac {1}{T}}+{\frac {(x_{0}-{\overline {x}})^{2}}{\sum \nolimits _{t=1}^{T}(x_{t}-{\overline {x}})^{2}}}\right)}}\;;\;{\hat {y}}_{0}+t_{1-\alpha /2;T-K}\cdot {\sqrt {\sigma ^{2}\left(1+{\frac {1}{T}}+{\frac {(x_{0}-{\overline {x}})^{2}}{\sum \nolimits _{t=1}^{T}(x_{t}-{\overline {x}})^{2}}}\right)}}\right]$

Aus dieser Form des Vorhersageintervalls erkennt man sofort, dass das Vorhersageintervall breiter wird, wenn sich die exogene Vorhersagevariable $x_{0}$ vom „Gravitationszentrum“ der Daten entfernt. Schätzungen der endogenen Variablen sollten also im Beobachtungsraum der Daten liegen, sonst werden sie sehr unzuverlässig.

Das verallgemeinerte Modell der linearen Mehrfachregression

Beim verallgemeinerten Modell der linearen Mehrfachregression wird für die Strukturbeziehung $\mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }},$ zugelassen, dass die Störgrößen heteroskedastisch und autokorreliert sind. Die Kovarianzmatrix des Störgrößenvektors ist dann nicht wie gewöhnlich unter den Gauß-Markow-Annahmen $\operatorname {Cov} ({\boldsymbol {\varepsilon }})=\sigma ^{2}\mathbf {I} _{T}$ , sondern hat die Struktur $\operatorname {Cov} ({\boldsymbol {\varepsilon }})=\mathbb {E} ({\boldsymbol {\varepsilon }}{\boldsymbol {\varepsilon }}^{\top })=\sigma ^{2}\mathbf {\Psi } =\mathbf {\Phi }$ , wobei $\mathbf {\Psi }$ als eine beliebige bekannte reelle nichtsinguläre positiv definite $T \times T$ Matrix angenommen wird und $\sigma ^{2}$ ein noch unbekannter Skalar darstellt. Das resultierende Modell $\mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }}$ mit ${\boldsymbol {\varepsilon }}\sim (\mathbf {0} ,\sigma ^{2}{\boldsymbol {\Psi }})$ nennt man verallgemeinertes (multiples) lineares Regressionsmodell (mit fixen Regressoren), kurz VLR.

Polynomiale Regression

Die polynomiale Regression ist ein Spezialfall der multiplen linearen Regression. Das multiple lineare Regressionsmodell wird auch zur Lösung von speziellen (im Hinblick auf die erklärenden Variablen) nichtlinearen Regressionsproblemen herangezogen. Bei der polynomialen Regression wird der Erwartungswert der abhängigen Variablen von den erklärenden Variablen mithilfe eines Polynoms vom Grade p > 1 , also durch die Funktionsgleichung

$\mu _{Y}=\beta _{1}+\beta _{2}x+\beta _{3}x^{2}+\ldots +\beta _{K}x^{p}$

beschrieben. Man erhält ein multiples lineares Regressionsmodell mit der oben genannten Regressionsfunktion, wenn man für die Potenzen von die Bezeichnungen $x=x_{2},\,x^{2}=x_{3},\,\ldots ,\,x^{p}=x_{K}$ einführt. Im Falle p=2 spricht man von quadratischer Regression.

Beispiel

Zur Illustration der multiplen Regression wird im folgenden Beispiel untersucht, wie die abhängige Variable : Bruttowertschöpfung (in Preisen von 95; bereinigt, Mrd. Euro) von den unabhängigen Variablen „Bruttowertschöpfung nach Wirtschaftsbereichen Deutschland (in jeweiligen Preisen; Mrd. EUR)“ abhängt. Da man in der Regel die Berechnung eines Regressionsmodells am Computer durchführt, wird in diesem Beispiel exemplarisch dargestellt, wie eine multiple Regression mit der Statistik-Software R durchgeführt werden kann.

Variable	Beschreibung der Variablen
${\text{BWSb95}}$	Bruttowertschöpfung in Preisen von 95 (bereinigt)
${\text{BBLandFF}}$	Bruttowertschöpfung von Land- und Forstwirtschaft, Fischerei
${\text{BBProdG}}$	Bruttowertschöpfung des produzierenden Gewerbes ohne Baugewerbe
${\text{BBBau}}$	Bruttowertschöpfung im Baugewerbe
${\text{BBHandGV}}$	Bruttowertschöpfung von Handel, Gastgewerbe und Verkehr
${\text{BBFinVerm}}$	Bruttowertschöpfung durch Finanzierung, Vermietung und Unternehmensdienstleister
${\text{BBDienstOEP}}$	Bruttowertschöpfung von öffentlichen und privaten Dienstleistern

Zunächst lässt man sich ein Streudiagramm ausgeben. Es zeigt, dass die gesamte Wertschöpfung offensichtlich mit den Wertschöpfungen der wirtschaftlichen Bereiche positiv korreliert ist. Das erkennt man daran, dass die Datenpunkte in der ersten Spalte der Grafik in etwa auf einer Geraden mit einer positiven Steigung liegen. Auffällig ist, dass die Wertschöpfung im Baugewerbe negativ mit den anderen Sektoren korreliert. Dies erkennt man daran, dass in der vierten Spalte die Datenpunkte näherungsweise auf einer Geraden mit einer negativen Steigung liegen.

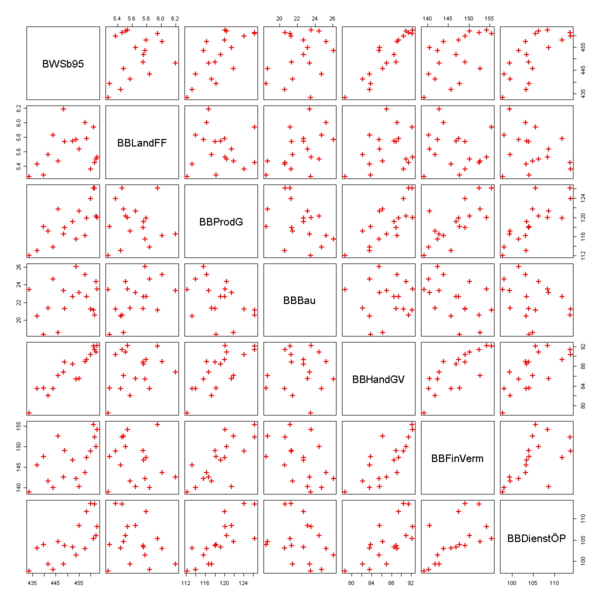
In einem ersten Schritt gibt man das Modell mit allen Regressoren in R ein:

lm(BWSb95~BBLandFF+BBProdG+BBBau+BBHandGV+BBFinVerm+BBDienstÖP)

Anschließend lässt man sich in R ein Summary des Modells mit allen Regressoren ausgeben, dann erhält man folgende Auflistung:

Residuals:
    Min     1Q      Median  3Q     Max
    −1.5465 −0.8342 −0.1684 0.5747 1.5564

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 145.6533 30.1373 4.833 0.000525 ***
BBLandFF      0.4952  2.4182 0.205 0.841493
BBProdG       0.9315  0.1525 6.107 7.67e−05 ***
BBBau         2.1671  0.2961 7.319 1.51e−05 ***
BBHandGV      0.9697  0.3889 2.494 0.029840 *
BBFinVerm     0.1118  0.2186 0.512 0.619045
BBDienstÖP    0.4053  0.1687 2.402 0.035086 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.222 on 11 degrees of freedom
Multiple R-Squared: 0.9889, Adjusted R-squared: 0.9828
F-statistic: 162.9 on 6 and 11 DF, p-value: 4.306e−10

Der globale F-Test ergibt eine Prüfgröße von $F=162{,}9$ . Diese Prüfgröße hat einen p-Wert von $4{,}306\cdot 10^{{-10}}$ , somit ist die Anpassung signifikant gut.

Die Analyse der einzelnen Beiträge der Variablen (Tabelle Coefficients) des Regressionsmodells ergibt bei einem Signifikanzniveau von $\alpha=0{,}05$ , dass die Variablen ${\text{BBLandFF}}$ und ${\text{BBFinVerm}}$ offensichtlich die Variable ${\text{BWSb95}}$ nur unzureichend erklären können. Dies erkennt man daran, dass die zugehörigen -Werte zu diesen beiden Variablen verhältnismäßig klein sind, und somit die Hypothese, dass die Koeffizienten dieser Variablen null sind, nicht verworfen werden kann.

Die Variablen ${\text{BBHandGV}}$ und ${\text{BBDienstOEP}}$ sind gerade noch signifikant. Besonders stark korreliert ist (in diesem Beispiel also ${\text{BWSb95}}$ ) mit den Variablen ${\text{BBProdG}}$ und ${\text{BBBau}}$ , was man an den zugehörigen hohen -Werten erkennen kann.

Im nächsten Schritt werden die nicht-signifikanten Regressoren ${\text{BBLandFF}}$ und ${\text{BBFinVerm}}$ aus dem Modell entfernt:

lm(BWSb95~BBProdG+BBBau+BBHandGV+BBDienstÖP)

Anschließend lässt man sich wiederum ein Summary des Modells ausgeben, dann erhält man folgende Auflistung:

Residuals:
     Min      1Q       Median   3Q      Max
     −1.34447 −0.96533 −0.05579 0.82701 1.42914

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) 158.00900 10.87649 14.528 2.05e−09 ***
BBProdG       0.93203  0.14115  6.603 1.71e−05 ***
BBBau         2.03613  0.16513 12.330 1.51e−08 ***
BBHandGV      1.13213  0.13256  8.540 1.09e−06 ***
BBDienstÖP    0.36285  0.09543  3.802 0.0022 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.14 on 13 degrees of freedom
Multiple R-Squared: 0.9886, Adjusted R-squared: 0.985
F-statistic: 280.8 on 4 and 13 DF, p-value: 1.783e−12

Dieses Modell liefert eine Prüfgröße von $F=280{,}8$ . Diese Prüfgröße hat einen p-Wert von $1{,}783\cdot 10^{{-12}}$ , somit ist die Anpassung besser als im ersten Modell. Dies ist vor allem darauf zurückzuführen, dass in dem jetzigen Modell alle Regressoren signifikant sind.

Basierend auf einem Artikel in:

Wikipedia.de