Primfaktorzerlegung
Die Primfaktorzerlegung ist die Darstellung einer natürlichen Zahl
als Produkt
aus Primzahlen, die dann als
Primfaktoren von
bezeichnet werden. Diese Darstellung ist (bis auf die Reihenfolge der Faktoren)
eindeutig und zählt zu den grundlegenden und klassischen Werkzeugen der Zahlentheorie. Sie ist
Gegenstand des Fundamentalsatzes
der Arithmetik. Es ist bisher kein effizientes
Faktorisierungsverfahren
bekannt, um die Primfaktorzerlegung einer beliebigen Zahl zu erhalten.
Definitionen
Sei
eine natürliche Zahl. Eine Zahl
heißt Primfaktor von
,
Die Primfaktorzerlegung ist die Darstellung der Zahl
als Produkt ihrer Primfaktoren. Da die Multiplikation
kommutativ
und assoziativ
ist, ist die Reihenfolge der Primfaktoren aus Sicht der Zahlentheorie unwichtig.
Die Primfaktorzerlegung der Eins
kann als leeres
Produkt betrachtet werden. Wenn
selbst eine Primzahl ist, so ist sie selbst ihr einziger Primfaktor. Gibt es
mehr als einen Primfaktor, so wird
zusammengesetzte
Zahl genannt. Die Null ist niemals Teil der multiplikativen
Gruppe und wird von solchen Betrachtungen ausgeschlossen. Ein Primfaktor
kann mehrfach auftreten; mehrfach auftretende Primfaktoren können mittels Exponenten-Schreibweise
zusammengefasst werden. Sind die Primfaktoren aufsteigend geordnet, spricht man
auch von der kanonischen Primfaktorzerlegung:
Unter den
Primfaktoren sind
verschiedene.
Der Exponent
eines Primfaktors
ist die Vielfachheit von
in
und wird auch als
-Bewertung von
bezeichnet. Er gibt an, wie oft
durch
teilbar ist.
Beispiele für Primfaktorzerlegungen
(Primzahl)
(Zweierpotenz)
, mit der kanonischen Darstellung
(Zehnerpotenz)
Fundamentalsatz der Arithmetik
Die Aussagen für Existenz der Primfaktorzerlegung für jede natürliche Zahl und deren Eindeutigkeit in der kanonischen Darstellung sind der Fundamentalsatz der Arithmetik, auch Hauptsatz der elementaren Zahlentheorie genannt. Beide Aussagen werden getrennt formuliert und bewiesen. Die Beweise sind elementar, werden klassisch als Widerspruchsbeweis formuliert und nutzen die Wohlordnung der natürlichen Zahlen. Zum ersten Mal vollständig und korrekt bewiesen findet sich der Fundamentalsatz der Arithmetik in den Disquisitiones Arithmeticae von Carl Friedrich Gauß. Er war aber bereits — wenn auch in leicht abgewandelter Form — Euklid bekannt.
Beweis der Existenz
Der Eins wird das leere Produkt zugeordnet und jede Primzahl stellt selbst ihre Primfaktorzerlegung dar. Damit bleibt zu zeigen, dass alle restlichen natürlichen Zahlen tatsächlich aus Primfaktoren zusammengesetzt sind.
Angenommen, es gibt Zahlen, die sich nicht als Produkt von Primzahlen
darstellen lassen, dann gibt es auch eine kleinste solche Zahl (genannt
),
aufgrund der Wohlordnung von
.
Da
dann weder die Eins noch eine Primzahl ist, besitzt
einen nichttrivialen Teiler,
das heißt, es existieren zwei natürliche Zahlen
mit
und beide sind größer als Eins und kleiner als
.
Da
die kleinste Zahl ist, die kein Produkt von Primfaktoren ist, müssen
und
also Primfaktorzerlegungen haben, etwa
und
.
Dann ist aber
auch eine Primfaktorzerlegung von
,
im Widerspruch zur Annahme.
Beweis der Eindeutigkeit
Angenommen, es gibt natürliche Zahlen mit jeweils mehreren unterschiedlichen
Zerlegungen, dann auch wieder eine kleinste, genannt .
Dies kann keine Primzahl sein und zwei Zerlegungen von
können keinen gemeinsamen Primfaktor
enthalten, da dann auch
zwei verschiedene Zerlegungen hätte und kleiner als
wäre, im Widerspruch zur Annahme, dass
minimal ist. Es gilt also etwa
,
wobei
und
Primzahlen sind, und es gilt
.
Das abschließende Argument ist das Lemma
von Euklid: Teilt eine Primzahl ein Produkt, so auch einen der Faktoren. Da
durch
teilbar ist, muss einer der Faktoren der anderen Zerlegung durch
teilbar sein und das ist
,
denn
ist prim. Also taucht ein beliebiger Primfaktor stets in beiden Zerlegungen auf
und damit sind sie identisch.
Eigenschaften
und
können keine gemeinsamen Primfaktoren haben.
- Um die Primfaktorzerlegung einer Zahl zu berechnen, stehen mehrere Faktorisierungsverfahren zur Verfügung, die nichttriviale Teiler ganzer Zahlen berechnen. Diese Aufgabenstellung ist als Faktorisierungsproblem für ganze Zahlen bekannt und kann mit den bisher bekannten Methoden nicht effizient berechnet werden, worauf weltweit Sicherheitskonzepte beruhen, insbesondere in der modernen Kryptographie. Siehe auch Primzahltest.
- Godfrey Harold Hardy
bewies mehrere erstaunliche statistische
Erkenntnisse zum Thema, unter anderem, dass die durchschnittliche Anzahl von
Primfaktoren für größer werdendes
nur sehr langsam anwächst und zwar wie
, also der doppelt angewendete natürliche Logarithmus. Der Satz von Erdős-Kac besagt darüber hinaus, dass die Anzahl der Primfaktoren asymptotisch normalverteilt ist mit einem Erwartungswert
und einer Standardabweichung
. (Zur Notation siehe Landau-Symbole.)
- Die Funktion
, die jede natürliche Zahl auf die Anzahl ihrer paarweise verschiedenen Primfaktoren abbildet, ist ein Beispiel für eine arithmetische Funktion, die additiv aber nicht streng additiv ist. Sie ist zu unterscheiden von der Teileranzahlfunktion, die alle Teiler einer Zahl zählt, nicht nur die Primteiler. Beispielsweise ist
, denn die Primfaktorzerlegung enthält zwei verschiedene Primzahlen: 2 und 5. Mit obiger Definition gilt:
.
- Der asymptotische arithmetische Mittelwert der maximalen Exponenten der Primfaktorzerlegungen der Zahlen 1, 2, 3, … ist die Niven-Konstante (rund 1,7), der asymptotische arithmetische Mittelwert der minimalen Exponenten ist genau 1.
- Der asymptotische Erwartungswert der relativen Anzahl der Ziffern des
größten Primfaktors einer Zahl wird durch die Golomb-Dickman-Konstante
angegeben.
Verallgemeinerung
Es gibt mehrere Möglichkeiten, Primzahlen zu verallgemeinern. Die bekannteste Anwendung sind die ganzen Zahlen, Primzahlen können dort auch ein negatives Vorzeichen haben. Andererseits ist dies schon ein spezielles Beispiel, da auch dort die Primfaktorzerlegung (bis auf Vorzeichen und Reihenfolge) eindeutig ist.
Ein allgemeiner Ansatz verlangt mindestens einen Begriff der Teilbarkeit innerhalb der mathematischen Struktur. David Hilbert bewies, dass für die gewünschte Eindeutigkeit eine additive Struktur zwingend notwendig ist. Üblicherweise wird von einem kommutativen Ring mit Eins ausgegangen, dort können Primelemente definiert werden: Ein Element ist prim, wenn Euklids Lemma dafür gilt. Damit ist nicht garantiert, dass es für alle Elemente des Rings Zerlegungen in Primelemente gibt, aber wenn es welche gibt, dann sind sie eindeutig. Um die Existenz zu sichern, ist eine weitere Eigenschaft notwendig: die Unzerlegbarkeit. Um die definieren zu können, schränkt man die Struktur weiter ein und betrachtet nullteilerfreie Ringe (also Integritätsringe), dort können zusätzlich irreduzible Elemente definiert werden, die aber nicht prim genannt werden können. Sie sind unzerlegbar und enthalten die Primelemente als Teilmenge.
Zerlegungen in irreduzible Elemente in einem Integritätsring sind nicht notwendigerweise eindeutig. Um eine Struktur zu erhalten, in der die Produkt-Zerlegungen eindeutig sind, muss man diese Eindeutigkeit explizit fordern, was zur Definition von faktoriellen Ringen führt. Mit dieser Forderung lässt sich dann aber dort auch schon die Äquivalenz von irreduzibel und prim folgern: Faktorielle Ringe sind ZPE-Ringe. Ein etwas anderer Ansatz wird mit Primideale verfolgt.
Beispiele
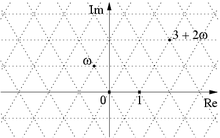
- In dem Integritätsring
sind die Elemente
keine Primelemente aber irreduzibel, und keine zwei sind zueinander assoziiert. Es gilt:
. Man kann also nicht von einer Primfaktorzerlegung sprechen.
- Ein irreduzibles
Polynom heißt Primpolynom,
wenn der Leitkoeffizient
gleich
ist. Im Polynomring
über einem Körper
ist jedes nichtkonstante Polynom im Wesentlichen eindeutig als Produkt von Primpolynomen darstellbar.
- Sowohl in den gaußschen Zahlen als auch den Eisenstein-Zahlen existiert stets eine Primfaktorzerlegung (außer für die 0).
Praktische Anwendung
Aus der Primfaktorenzerlegung lässt sich erkennen, ob eine Zahl durch eine andere teilbar ist. Das kleinste gemeinsame Vielfache (kgV) und der größte gemeinsame Teiler (ggT) können leicht aus der Primfaktorzerlegung bestimmt werden. In der Bruchrechnung können Brüche durch den ggT von Zähler und Nenner gekürzt werden. Beim Addieren und Subtrahieren werden zwei Brüche auf das kgV der Nenner erweitert.
Kryptographie
Eine wichtige Rolle spielen Primzahlen in der Kryptographie. Verschlüsselungssysteme wie RSA basieren darauf, dass kein effizientes Faktorisierungsverfahren bekannt ist. So ist es innerhalb von Sekunden problemlos möglich, zwei 500-stellige Primzahlen zu finden und miteinander zu multiplizieren. Mit den heutigen Methoden würde die Rückgewinnung der beiden Primfaktoren aus diesem 999- oder 1000-stelligen Produkt dagegen sehr lange Zeit dauern.
Gödelnummern
Für jede Aufzählung von Primzahlen
ohne Wiederholung ist die durch
definierte Abbildung aller Tupel ganzer Zahlen
injektiv und berechenbar, durch Primfaktorzerlegung ist die Umkehrfunktion
ebenfalls berechenbar. Die Abbildung eignet sich daher zur Definition von Gödelnummern.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 31.07. 2022