Eisenstein-Zahl

Die Eisenstein-Zahlen sind eine Verallgemeinerung der ganzen Zahlen auf die komplexen Zahlen. Sie
sind nach dem deutschen Mathematiker
Gotthold Eisenstein, einem Schüler von Gauß,
benannt. Die gaußschen
Zahlen sind eine andere Verallgemeinerung der ganzen Zahlen auf die
komplexen Zahlen. Die Eisenstein-Zahlen sind der Ganzheitsring,
also die Maximalordnung
des quadratischen
Zahlkörpers ,
der mit dem 3. Kreisteilungskörper
übereinstimmt. Sie treten beispielsweise bei der Formulierung des kubischen
Reziprozitätsgesetzes auf (→ siehe Kubisches Reziprozitätsgesetz in diesem Artikel).
Definition
Eine komplexe Zahl
ist eine Eisenstein-Zahl, wenn sie sich in der Form
mit
und ganzen Zahlen
und
darstellen lässt.
ist eine (primitive) dritte Einheitswurzel
und erfüllt somit die Gleichung
Im Folgenden bezeichnet
immer genau die oben genannte primitive Einheitswurzel, nicht die zu
konjugiert komplexe zweite Nullstelle dieser quadratischen Gleichung.
Mit anderen Worten: Die Eisensteinzahlen bilden den Ring ,
der aus dem Ring der ganzen Zahlen durch Adjunktion
der primitiven 3. Einheitswurzel
entsteht. Der Ganzheitsring des Kreisteilungskörpers, der aus
durch Adjunktion einer primitiven 6. Einheitswurzel, zum Beispiel
durch Adjunktion des Hauptwertes
entsteht,
,
stimmt ebenfalls mit den Eisenstein-Zahlen überein.
Geometrische Bedeutung
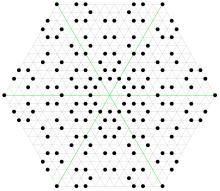
Die Eisenstein-Zahlen bilden ein Dreiecksgitter in der gaußschen Zahlenebene. Sie entsprechen den Mittelpunkten einer dichtesten Kugelpackung in zwei Dimensionen.
Zahlentheorie
Auf den Eisenstein-Zahlen lässt sich Zahlentheorie
betreiben: Die Einheiten
sind genau die sechs komplexen Nullstellen der Gleichung ,
die zyklische
Einheitengruppe
wird also von jeder der beiden primitiven 6. Einheitswurzeln
bzw.
erzeugt. Zu jeder von
verschiedenen Eisensteinzahl
existieren genau sechs assoziierte
Elemente, die in der multiplikativen Gruppe des Körpers
eine Nebenklasse
bilden.
Man kann Primelemente
analog zu den Primzahlen in
definieren und zeigen, dass die Primfaktorzerlegung einer Eisenstein-Zahl –
bis auf Assoziiertheit und Reihenfolge der Primfaktoren – eindeutig ist.
Die Eisensteinzahlen bilden also einen faktoriellen
Integritätsbereich. Alle ganzen Zahlen der Form
sind in den Eisenstein-Zahlen zerlegbar.
Dort sind daher die Zahlen 3, 7, 13, 19, … keine Primelemente.
Genauer treten die folgenden drei Fälle auf:
- 3 ist ein Sonderfall:
. Dies ist die einzige Primzahl in
, die durch das Quadrat eines Primelementes in
teilbar ist. Man sagt in der algebraischen Zahlentheorie, diese Primzahl sei verzweigt.
- Positive Primzahlen
, die die Kongruenz
erfüllen, bleiben auch in
prim. So eine Primzahl nennt man träge.
- Positive Primzahlen
, die die Kongruenz
erfüllen, werden in
zu Produkten von zwei zueinander komplex konjugierten Primelementen Man sagt, solche Primzahlen seien zerlegt.
Die trägen Primzahlen sind also
und eine Primfaktorisierung der ersten zerlegten Primzahlen lautet:
Die sechs mit einem Primelement assoziierten Elemente sind prim, ebenso das
zu einem Primelement
komplex
konjugierte Element
.
Da die Norm
eines Elementes von
stets in
liegt, bilden
,
die trägen ganzen Primzahlen und die Primelemente, die als Faktoren bei der
Zerlegung der zerlegten ganzen Primzahlen auftreten, zusammen mit ihren
Assoziierten die Menge aller Primelemente in
.
Der Ring der Eisenstein-Zahlen ist euklidisch.
Kubischer Rest-Charakter
Im Ring der Eisensteinschen Zahlen gilt ein Satz, der analog zum kleinen fermatschen Satz der elementaren Zahlentheorie ist:
Sind
und
ein Primelement, das
nicht teilt, dann gilt:
Wenn nun für die Norm von
gilt, dass
und also IMG class="text"
style="width: 20.18ex; height: 2.84ex; vertical-align: -0.83ex;"
alt="N(\rho )\equiv 1{\pmod 3}" src="/svg/200bef9739d79ea29260e473bd271c9688f3a55f.svg">
ist, dann ist
eine Potenz mit ganzzahligem Exponenten und es gilt:
für eine eindeutig bestimmte 3. Einheitswurzel
Man nennt diese Einheitswurzel den kubischen Rest-Charakter von
modulo
und schreibt dafür:
Die Bezeichnung als Charakter ergibt sich daraus, dass die Abbildung
bei festem Primelement
einen unitären
Charakter auf der multiplikativen Gruppe des Körpers
bestimmt.
Die Kongruenz
ist in
genau dann lösbar, wenn
gilt. Ist die Kongruenz lösbar und
,
dann nennt man
einen kubischen Rest modulo
;
ist die Kongruenz unlösbar, einen kubischen Nichtrest modulo
.
Ebenso werden die Begriffe kubischer Rest und Nichtrest allgemeiner erklärt,
wenn
zwar teilerfremd zu
,
aber kein Primelement ist.
Der kubische Rest-Charakter hat für Primelemente ,
die nicht zu
assoziiert sind, formale Eigenschaften, die den Eigenschaften des Legendre-Symbols
ähneln:
, wobei der Überstrich für die komplexe Konjugation steht.
- Sind
und
assoziierte Primelemente, dann gilt
.
- Ist
, dann gilt
.
Der kubische Rest-Charakter kann im „Nenner“ multiplikativ auf
zusammengesetzte Zahlen fortgesetzt werden, die teilerfremd zu 3 sind. Dabei
wird dann ergänzend definiert, dass das so definierte kubische Restsymbol
den Wert 0 hat, falls die Zahlen
im Ring der Eisenstein-Zahlen nicht zueinander teilerfremd sind, aber
teilerfremd zu 3 ist. Diese Verallgemeinerung ist analog zu der
Verallgemeinerung des Legendre-Symbols zum Jacobi-Symbol
bis auf die Tatsache, dass für den Fall, dass
gilt oder gleichwertig, dass die Norm von
in
von 3 geteilt wird, kein Wert für das Symbol definiert wird. Manchmal wird im
zuletzt genannten Fall das Symbol 0 gesetzt. Diese Variante ändert an den
folgenden Aussagen nichts.
Ähnlich wie beim Jacobi-Symbol gelten für einen „Nenner“
des kubischen Restsymbols, der kein Primelement ist, folgende Aussagen:
- Durch die multiplikative Fortsetzung gilt nach Definition:
-
es eine Zerlegung
von
in paarweise verschiedene Primelemente
hat, von denen keines zu
assoziiert ist.
- Ist der „Zähler“
ein kubischer Rest modulo
und
, dann nimmt das Symbol den Wert 1 an.
- Nimmt das Symbol einen von 1 verschiedenen Wert an, dann ist der Zähler
kein kubischer Rest modulo
oder
nicht teilerfremd zu 3.
- Das Symbol kann den Wert 1 annehmen, auch wenn der Zähler ein kubischer
Nichtrest modulo
ist.
Primäre Zahlen
Zur Formulierung eines kubischen Reziprozitätsgesetzes auf dem Ring der
Eisenstein-Zahlen müssen aus den Assoziierten einer Eisensteinzahl bestimmte
Vertreter ausgewählt werden. Eisenstein nennt eine Zahl
primär, wenn sie die Kongruenz
erfüllt. Man kann leicht nachweisen, dass für Zahlen, deren Norm (in
)
teilerfremd zu 3 ist, genau ein zu ihnen assoziiertes Element primär im Sinne
dieser Definition ist. Ein Nachteil der Definition ist, dass das Produkt zweier
primärer Zahlen immer die Gegenzahl einer primären Zahl ist.
Man definiert daher heute meistens:
- Eine Eisenstein-Zahl
ist primär, wenn sie zu 3 teilerfremd ist und modulo
zu einer gewöhnlichen ganzen Zahl kongruent ist.
Diese Definition ist gleichbedeutend damit, dass die Kongruenz
im Ring der Eisensteinzahlen gilt. Es gilt dann:
- Falls die Norm von
teilerfremd zu 3 ist, dann ist genau eine der Zahlen
primär.
- Das Produkt von zwei primären Zahlen ist primär.
- Mit jeder Zahl ist auch die zu ihr konjugiert komplexe Zahl primär.
- Eine im modernen Sinn primäre Zahl
ist entweder selbst primär im Sinn von Eisenstein oder
ist es.
- Unter den Assoziierten einer Zahl, die teilerfremd zu 3 ist, sind stets
genau zwei primäre Zahlen
.
Da −1 immer ein kubischer Rest ist, reicht die Eindeutigkeit dieser Definition „bis auf das Vorzeichen“ für die Formulierung des Reziprozitätsgesetzes aus.
Kubisches Reziprozitätsgesetz
Für zwei primäre Zahlen
gilt:
Zu diesem kubischen Reziprozitätsgesetz gibt es Ergänzungssätze für
die Einheiten und das Primelement :
Falls
primär ist und
gilt, dann gilt auch
Für primäre „Nenner“
mit
kann
durch das assoziierte primäre Element
ersetzt werden, ohne dass sich der Wert des Symbols ändert.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.10. 2022