Linse (Optik)

Einfache bikonvexe Linse (Sammellinse)

Als Linsen bezeichnet man in der Optik transparente Scheiben, von deren zwei Oberflächen wenigstens eine – meistens kugelig bzw. sphärisch – gekrümmt ist. Durchgehendes Licht wird an den Oberflächen gebrochen und abgelenkt oder gesammelt(Sammellinse) oder nach außen gestreut. Eine konvexe Oberfläche sammelt, eine konkave Oberfläche zerstreut das Licht.

Der Manginspiegel ist eine Kombination aus einer Linse und einem Spiegel. Die zweite Oberfläche ist verspiegelt, wodurch das Licht zurückgeworfen wird. Die zusätzliche Ablenkung (Sammeln/Zerstreuen) durch Spiegeln entspricht dem Brechen an der unverspiegelten zweiten Fläche.

Zur Korrektur von Abbildungsfehlern werden einzelne Linsen miteinander kombiniert. Dabei werden oft zwei oder mehrere Linsen miteinander verkittet (die entsprechenden Kontaktstellen haben die gleiche Krümmung), so dass wie Einzellinsen zu behandelnde Linsengruppen entstehen.

Dünne Linse

Eine dünne Linse ist eine optische Linse, deren Dicke klein ist im Vergleich zu den Radien ihrer brechenden Oberflächen.

In der paraxialen Optik ist die dünne Linse ein Konzept, nach dem die endlich dicke reale Linse durch eine Ebene ersetzt wird. Die beiden Brechvorgänge von einem Lichtstrahl an den Grenzflächen werden zu einem Brechvorgang an dieser Ebene zusammengefasst. Wenn die reale Linse einen symmetrischen Querschnitt hat (z.B. bikonvex oder bikonkav), so wird ihre Mittelebene zur brechenden Ebene. Ein Lichtstrahl, der auf den Mittelpunkt der Ebene trifft, geht mit unveränderter Richtung und ohne Parallelversatz durch die Linse hindurch.

Das Konzept der dünnen Linse ist eine Idealisierung der endlich dicken realen Linse und eine gute Näherung bei großen Radien ihrer Grenzflächen und damit auch großer Brennweite. Die formale Reduktion auf eine Ebene bedeutet nicht, dass die Linse keinen Brechungsindex oder keine gekrümmten Grenzflächen hat, denn von beidem hängt ihre Brennweite ab. Zur Beschreibung des Verhaltens der dünnen Linse genügt aber ihre Brennweite.

Optische Abbildung mittels einer dünnen Linse

Abbildung 1: Eine bikonvexe dünne Linse

Die zwei Hauptebenen $H_{1}$ und $H_{2}$ eines allgemeinen optischen Systems fallen bei der dünnen Linse in ihrer Ersatzebene (Mittelebene) zusammen. Die dünne Linse hat nur eine Hauptebene . Beide Brennweiten $\overline {OF}$ und $\overline {OF'}$ werden von der Hauptebene aus gemessen. Die strahlenoptische Konstruktion der optischen Abbildung ist etwas einfacher und geschieht wie folgt.

Der Bildpunkt B’ wird mit Hilfe von zwei der drei Hauptstrahlen Parallelstrahl (1), Mittelpunktstrahl (3) oder Brennpunktstrahl (2) (in Abbildung 1 von oben nach unten, die vom Gegenstandspunkt B ausgehen, gefunden. Die Strahlen werden nur einmal – nämlich an der Mittel/Haupt-Ebene – gebrochen (Strahl (3) bleibt ungebrochen). Der Parallelstrahl wird so gebrochen, dass er durch den bildseitigen Brennpunkt F’ geht. Der Brennpunktstrahl geht durch den gegenstandsseitigen Brennpunkt F und wird an der Mittelebene so gebrochen, dass er zum Parallelstrahl auf der Bildseite wird.

Grundlegende Eigenschaften

Radien einer Sammellinse: +R₁ (R₁> 0) ; −R₂ (R₂< 0)

Radien einer Zerstreuungslinse: -R₁ (R₁<0) ; +R₂ (R₂> 0)

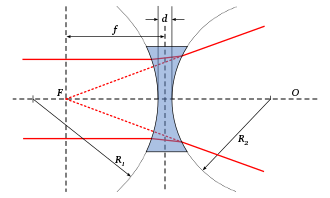
Dünne sphärische Linsen lassen sich durch folgende geometrische und Material-Eigenschaften beschreiben:

den Durchmesser der Linse
die Krümmungsradien der Eintrittsfläche $\textstyle R_{1}$ und der Austrittsfläche $\textstyle R_{2}$ und
den Brechungsindex $\textstyle n'$ des Linsenmaterials.

Aus diesen lassen sich in Verbindung mit dem Brechungsindex des Umgebungsmaterials $\textstyle n$ die Brennweite $\textstyle f$ und der Brechwert $\textstyle D$ als wichtigste optische Eigenschaften ableiten:

$D={\frac {1}{f}}={\frac {n'-n}{n}}\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right)$ .

Dies ist die sogenannte Linsenschleiferformel, die in guter Näherung für dünne Linsen gilt (d.h. die Dicke der Linse ist wesentlich kleiner als beide Kugelradien). Die untenstehende, exakte Variante berücksichtigt auch die Linsendicke, falls diese nicht mehr vernachlässigbar ist.

Dicke Linsen – das sind insbesondere Linsen, die an ihrer dünnsten Stelle eine endliche Dicke haben – erfordern zusätzlich die Angabe:

die Dicke der Linse in der Mitte $\textstyle d$

Eine dicke Linse weist bei sonst gleichen Parametern eine andere Brennweite als eine dünne Linse auf; weiterhin entstehen zwei nicht mehr aufeinanderliegende Hauptebenen, da der Strahlversatz beim (nicht achsparallelen) Durchgang durch die Linse nicht mehr vernachlässigt werden kann:

$D={\frac {1}{f}}={\frac {n'-n}{n}}\left({\frac {1}{R_{1}}}-{\frac {1}{R_{2}}}\right)+{\frac {(n'-n)^{2}\,d}{n\,n'\,R_{1}\,R_{2}}}$ .

Bezeichnet man mit $D_{1}={\frac {n'-n}{n}}\cdot {\frac {1}{R_{1}}}$ und $D_{2}=-{\frac {n'-n}{n}}\cdot {\frac {1}{R_{2}}}$ die Brechwerte von Vorder- bzw. Rückfläche der Linse, lässt sich der Gesamtbrechwert der Linse als

$D=D_{1}+D_{2}-{\frac {n}{n'}}dD_{1}D_{2}$

schreiben, was insbesondere in der Augenoptik als Gullstrand-Formel bekannt ist.

Weiterhin ergibt sich aus den Krümmungsradien die äußere Erscheinungsform der Linse, d.h. ob es sich um eine (bi)konkave oder (bi)konvexe Linse oder um eine der anderen Formen handelt.

Genauere Betrachtungen führen zum Thema der prinzipiell unvermeidbaren Abbildungsfehler und weiterer Fehler durch Fehler und Ungenauigkeiten bei der Herstellung (Materialfehler, Toleranzen beim Schliff, Montagefehler).

Herstellung und verwendete Materialien

Linsen zur Verwendung im sichtbaren Spektralbereich werden aus optischen Gläsern oder Kunststoffen wie Polycarbonaten, Polymethylmethacrylaten oder Cyclo-Olefin-(Co)polymeren hergestellt. Weiterhin ist im Gegensatz zu diesen amorphen auch die Verwendung von kristallinen Materialien möglich, wie Calciumfluorid oder Saphir.

Rohlinge für Glaslinsen werden je nach Größe und Qualitätsanforderungen unterschiedlich hergestellt:

klein, geringe Anforderungen:
- Herstellen der Linsen direkt durch Heißpressen
- Es entstehen Inhomogenitäten im Brechungsindex, die auch noch anisotrop sind, durch entstehende mechanische Spannungen
- können durch nachträgliches Tempern reduziert werden
höhere Anforderungen (Präzisionsoptiken):
- Urformen: Glasblöcke werden gegossen und langsam abgekühlt. Abkühldauer bei Grobkühlung: einige Tage, Feinkühlung: etliche Wochen bis wenige Monate
- Trennschleifen: Glasblöcke werden durch Trennschleifen zerteilt: mittels Kreisfräsen in Zylinder, diese werden dann weiter in Scheiben zerlegt.

Daran schließt sich das Schleifen und Polieren an:

Grobschleifen mittels Fräsen (verbleibendes Aufmaß: 100 bis 200 µm)
Feinschleifen/Läppen mittels Diamantkörnern (verbleibendes Aufmaß: um 1 µm)
Polieren mittels Polierrot oder Ceroxid (Rauhigkeit: < λ/10)
Zentrieren (Abschleifen des Randes zum Festlegen der optischen Achse)
(bei durch Molding hergestellten asphärischen Linsen schließt sich hier eine Heißumformung an)

Bei geringeren Qualitätsanforderungen können die bei hohen Temperaturen gepressten Rohlinge direkt verwendet werden. Kunststofflinsen können durch Spritzgießen oder Spritzprägen wie auch durch klassisches Schleifen und Polieren hergestellt werden.

Mit Hilfe der geometrischen Größen Durchmesser, Linsenradien, Mittendicke, ergänzt mit Herstelltoleranzen (z.B. Passfehlertoleranz einschließlich durchschnittlicher Wellenfrontfehler), und der Materialeigenschaften Brechungsindex, Abbe-Zahl und Spannungsdoppelbrechung, ergänzt durch Materialtoleranzen (z.B. Homogenität), werden die optischen Eigenschaften einer sphärischen Linse vollständig beschrieben. Die wesentlichste Kenngröße einer Linse für ihre abbildende Funktion ist die Brennweite (Einheit: Meter), d.h. die Distanz zwischen Brennpunkt oder Brennebene und Hauptebenen. Der Kehrwert der Brennweite wird als Brechwert (Einheit: Dioptrien) angegeben. Der Durchmesser der nutzbaren Fläche einer Linse wird Öffnung oder Apertur genannt.

Eine wichtige Eigenschaft aller durch Strahlenoptik beschreibbaren Systeme ist das Prinzip der Umkehrung des Lichtweges: Wenn ein von einer Seite einfallender Lichtstrahl entlang seines Weges verfolgt wird, so wird ein entgegengesetzt einfallender Lichtstrahl diesen Weg genau umgekehrt durchlaufen.

Verschiedene Linsenformen

Sphärische Linsen

Bei den einfachsten Linsen sind die beiden optisch aktiven Flächen sphärisch. Das heißt, sie sind Oberflächenausschnitte einer Kugel. Man unterscheidet:

Bezeichnung von Linsen nach ihrer Brechkraft bzw. der Krümmung ihrer Flächen. Die konvex-konkav Linse ist hier spiegelverkehrt.

Sammellinsen mit zwei konvexen Flächen oder mit einer konvexen und einer ebenen Fläche, jedenfalls in der Mitte, im Bereich der optischen Achse, dicker als am Rand; ein Bündel parallel zur optischen Achse einfallender Lichtstrahlen wird idealerweise in einem Punkt hinter der Linse, dem Brennpunkt oder Fokus F, gesammelt. Ihre Brennweite f ist positiv.
Zerstreuungslinsen (Streulinse) mit zwei konkaven Flächen (bikonkav) oder mit einer konkaven und einer ebenen Fläche (plankonkav), jedenfalls am Rand dicker als in der Mitte; ein Bündel von einfallenden Parallelstrahlen läuft hinter der Linse so auseinander, als käme es von einem Punkt auf der Einfallseite des Lichts. Die Brennweite ist negativ.

In beiden Gruppen gibt es Linsen, die sowohl eine konkave als auch eine konvexe Fläche besitzen. Solche Linsen dienen oft zur Korrektur von Abbildungsfehlern in optischen Systemen mit mehreren Linsen. Es sind Sammellinsen, falls die konvexe Fläche stärker gekrümmt ist, oder Zerstreuungslinsen, falls die konkave Fläche stärker gekrümmt ist. Ursprünglich hießen nur erstere Meniskuslinsen (von griech. μηνίσκος mēnískos, Möndchen), während letztere heute als negative Menisken bezeichnet werden.

Ein Bauelement mit zwei planen und parallelen optisch wirksamen Flächen heißt Planplatte oder planparallele Platte.

Für das Rechnen nach den Regeln der geometrischen Optik werden nach DIN 1335 die in Lichtrichtung aufeinander folgenden Radien mit R₁ und R₂ (mit R₃ und R₄) bezeichnet. Das zugehörige Vorzeichen unterscheidet nicht direkt zwischen konvexer und konkaver Fläche. Der Radius einer Fläche ist positiv definiert, wenn das Licht zuerst die Fläche, dann ihren Krümmungsmittelpunkt passiert. Bei umgekehrter Reihenfolge ist der Radius negativ definiert. In graphischen Darstellungen kommt das Licht konventionell von links (oder von oben).

Für die drei Flächen konvex, plan (eben) oder konkav ergeben sich folgende Vorzeichen:

Konvexe Fläche (sie ist nach außen gewölbt): +R₁ (R₁ > 0) oder −R₂ (R₂ < 0).
Plane Fläche (ihre Krümmung ist null): R = ±_∞.
Konkave Fläche (sie ist nach innen gewölbt): −R₁ (R₁ < 0) oder +R₂ (R₂ > 0).

Die durch die Krümmungsmittelpunkte verlaufende Gerade wird als optische Achse O bezeichnet. Ist eine der beiden Linsenflächen plan, so steht die optische Achse senkrecht auf ihr.

Sphärische Linsen führen prinzipbedingt zu sphärischer Aberration, weil der Brennpunkt der Randstrahlen nicht mit dem Brennpunkt der achsnahen Strahlen übereinstimmt, gegebenenfalls auch abhängig von der Wellenlänge des Lichts. Um diese Fehler zu verringern, werden Linsensysteme (Anastigmate, Cooke-Triplet, Tessar) verwendet, die die Fehler weitgehend kompensieren.

Asphärische Linsen

→ Hauptartikel: Asphärische Linse

Asphärische Linsen weisen weitere Freiheitsgrade beim Design auf und ermöglichen eine bessere Korrektur eines optischen Systems als eine sphärische Linse. Viele Asphären haben nur geringe Abweichungen gegenüber einer Kugeloberfläche. Auf der anderen Seite gibt es auch Freiformlinsen mit komplexen nicht-rotationssymmetrischen Oberflächen. Nachteile asphärischer Linsen sind erhöhte Fertigungskosten und eine geringere Oberflächenqualität. Ein typischer Effekt sind Riefen (die man immer deutlich im Bokeh sieht), die entweder beim Schleifen selbst oder bei der Herstellung des Presswerkzeugs entstehen.

Eine weitere Kategorie sind Gradientenlinsen, in denen sich der Brechungsindex stetig räumlich ändert. Licht wird hier nicht nur an Grenzflächen, sondern auch im Glas selbst gebrochen. Mit ihnen können ähnliche Effekte wie mit Asphären erreicht werden.

Ideale Linse

Für zwei eingeschränkte Zwecke gibt es Linsenformen, die für monochromatisches Licht keinen Abbildungsfehler haben.

Exaktes Bündeln parallel zur optischen Achse einfallenden Lichts in einem Punkt:
Eine Möglichkeit ist, dass die dem einfallenden Licht zugewandten Fläche der Linse plan ist, und die abgewandte Seite die Form eines Hyperboloids hat. Für den halben Öffnungswinkel $\alpha$ des zum Hyperboloid gehörenden Asymptotenkegels muss $n\cdot \cos \alpha =1$ gelten, mit dem Brechungsindex des Linsenmaterials. Die einfallenden Strahlen werden gerade in einem der beiden Hyperbelbrennpunkte gebündelt – in jenem mit dem größeren Abstand zum Scheitel der Linse.
Gleich langer optischer Weg für alle Strahlen, die in einem Punkt auf der optischen Achse entspringen bis zum gemeinsamen Bildpunkt:
Die plane Fläche der Linse wird durch eine Sphäre um diesen Punkt und die hyperbolische Fläche durch ein kartesisches Oval ersetzt. Die Abbildung geschieht nach dem Fermatschen Prinzip. Für den Fall, dass benachbarte Punkte des Urbildes gleichmäßig auf benachbarte Punkte des Bildes abgebildet werden sollen, sind solche Überlegungen noch wesentlich komplexer.

Astigmatische Linsen

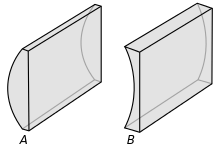
Zylinderlinse als Grenzfall einer astigmatischen Linse
A: Sammellinse, B: Zerstreuungslinse

Astigmatische Linsen haben in zwei senkrecht zueinander stehenden radialen Richtungen verschieden große Brennweiten. Grenzfall ist die Zylinderlinse, die in einer der beiden Richtungen planparallele Oberflächenkonturen hat und in ihrer typischen Form tatsächlich ein Zylinderabschnitt ist: eine zylindrische und eine plane Oberfläche. Sie bündelt parallel einfallendes Licht auf einer Brennlinie.

Astigmatische Linsen werden in folgenden Fällen eingesetzt:

Brillengläser, die Astigmatismus des menschlichen Auges ausgleichen,
Linsen in Objektiven für das anamorphotische Verfahren

Elastische Linsen

Elastische Linse bezeichnet ein Linse, die die Brechkraft durch die Verformung eines elastischen Festkörpers ändert. Es ergeben sich aus dem Funktionsprinzip folgende Vorteile:

Die Form der Grenzfläche ist frei wählbar (sphärisch, asphärisch).
Die Größe der Brechkraftänderung ist bei Verwendung von Gummimaterialien sehr groß (ca. 15 dpt).
Die Verformung kann sehr schnell erfolgen.

Dieses Wirkungsprinzip nutzt das Auge, wird aber auch gelegentlich in der Technik verwendet.

Brennweite und Hauptebenen

Brechung an einer sphärischen Grenzfläche: Abbesche Invariante

Die für eine optische Abbildung benutzte lichtbrechende Eigenschaft einer Linse hängt vom Brechungsindex ihres Materials und von der Form ihrer Grenzflächen ab. Beides zusammen drückt die Brennweite aus. Zusätzlich sind zwei Hauptebenen anzugeben, je eine gegenstands- und eine bildseitige als Bezugsebene für die gegenstands- bzw. die bildseitige Brennweite. Die beiden Brennweiten unterscheiden sich aber nur, wenn das optische Medium vor der Linse nicht mit dem nach der Linse identisch ist.

Sowohl die Brennweiten als auch die Hauptebenen sind ideale Größen, die sich beim Arbeiten nach dem Konzept der paraxialen Optik ergeben. Innerhalb dieses Konzeptes lassen sie sich aus den Material- und den geometrischen Eigenschaften theoretisch angeben, das heißt errechnen. Die Brechung wird an jeder der beiden Grenzflächen getrennt untersucht. Anschließend werden die Ergebnisse und die gegenseitige Lage der Flächen zu Gleichungen für die Größe der Brennweiten und die Lage der Hauptebenen zusammengefasst.

Brechung an einer einzelnen sphärischen Grenzfläche

Brennweite f' an einer sphärischen Grenzfläche

Die Brennweiten einer einzelnen sphärischen Grenzfläche sind in der Abbeschen Invariante, einer Grundgleichung der paraxialen Optik, mit enthalten. Eine der beiden Schnittweiten ist Brennweite, wenn die andere im Unendlichen liegt, aus dem parallel einfallendes Licht im Brennpunkt gesammelt wird.

Liegt die Schnittweite im Unendlichen, so wird zu , und aus der Abbeschen Invariante

$n\left({\frac {1}{r}}-{\frac {1}{s}}\right)=n'\left({\frac {1}{r}}-{\frac {1}{s'}}\right)$

wird:

$f'=r{\frac {n'}{n'-n}}$ .

Bei umgekehrter Strahlrichtung liegt die Schnittweite im Unendlichen, wird zu , und aus der Abbeschen Invariante wird:

$f=r{\frac {n}{n-n'}}$ .

Die Hauptebene geht durch den Scheitelpunkt der sphärischen Fläche.

Brechung an einer Linse

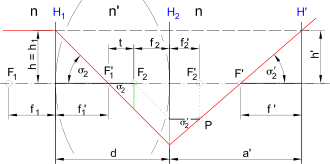
Brennpunkt und bildseitige Hauptebene für zwei Flächen

Bei einer Linse erfolgt die Brechung an zwei in der Regel sphärischen Grenzflächen. Die gemeinsame Brennweite lässt sich unter Beachtung folgender Vorgaben finden:

Die Abbildung des bildseitigen Brennpunkts der ersten Fläche durch die zweite Fläche ist der bildseitige Brennpunkt der Linse, denn alle einfallenden parallelen Strahlen passieren sowohl den einen als auch den anderen Punkt (roter Linienzug in nebenstehender Abbildung).
Die Verlängerung eines achsparallelen einfallenden Strahles schneidet sich mit dem gebrochen durch die Linse gehenden Strahl in der bildseitigen Hauptebene der Linse (unterbrochene Linie in nebenstehender Abbildung). Dem liegt die Definition der Hauptebenen zugrunde, dass der Abbildungsmaßstab zwischen ihnen 1 ist.

Ein Grundzusammenhang in der optischen Abbildung ist im Winkelverhältnis $\gamma '$ enthalten:

$\gamma '_{2}={\frac {\tan \sigma '_{2}}{\tan \sigma _{2}}}={\frac {t}{f'_{2}}}$ .

Damit lässt sich der Punkt P finden, durch den der rote Linienzug führen muss.

Die Gleichung für die bildseitige Brennweite der Linse lautet mit den Brennweiten $f'_{2},f_{2}$ und $f'_{1}$ der beiden Flächen und ihrem gegenseitigen Abstand :

$f'={\frac {f'_{1}f'_{2}}{d-f'_{1}-f_{2}}}$ .

Der Brechungsindex vor und nach der Linse sei gleich und betrage . Der Brechungsindex des Linsenmaterials ist . Die Brennweiten einer Fläche sind oben hergeleitet und lauten: $f_{1}'=r_{1}{\frac {n'}{n'-n}}$ , $f_{2}'=r_{2}{\frac {n}{n-n'}}=-r_{2}{\frac {n}{n'-n}}$ , $f_{2}=r_{2}{\frac {n'}{n'-n}}$ .
Mit diesen Angaben lautet das Schlussergebnis für die Brennweiten:

${\frac {1}{f'}}={\frac {1}{f}}={\frac {n'-n}{n}}\left({\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}\right)+{\frac {(n'-n)^{2}d}{n'nr_{1}r_{2}}}$ .

Die Brennweiten sind Funktionen des Linsenmaterials ( n'/n ) und der Linsengeometrie (Radien der Grenzflächen und Dicke).

Linse, allgemein: Gleichungen u.a. für Brennweite/n (1) und Lage der Hauptebenen (3) und (2)
ausgeführte Linse: Rechenergebnisse für Brennweiten und Lage der Hauptebenen

Wenn die Linse relativ dünn ist ( $d\ll r_{1},r_{2}$ ; bei der dünnen Linse ist definitionsgemäß d=0 ), verkürzt sich obige Gleichung zu

${\frac {1}{f}}={\frac {1}{f'}}={\frac {n'-n}{n}}\left({\frac {1}{r_{1}}}-{\frac {1}{r_{2}}}\right)$ .

Mit den oben genannten Vorgaben ist auch die Lage der Hauptebenen bestimmt.

Die Entfernung der bildseitigen Hauptebene vom Scheitelpunkt $H_{2}$ ( $S_{2}$ in nebenstehender Abbildung) der bildseitigen Fläche ist

${\overline {H_{2}H'}}={\frac {f'_{2}d}{d-f'_{1}-f_{2}}}$ .

Analoges gilt auf der Gegenstandsseite:

${\overline {H_{1}H}}={\frac {-f_{1}d}{d-f'_{1}-f_{2}}}$ .

Wenn die Linse relativ dünn ist ( $d\ll f'_{1},f_{2}$ ), werden diese Abstände zu null. Die Hauptebenen verbleiben auf den Scheiteln der Flächen.

Nebenstehende Abbildung enthält die Ergebnisse, nachdem die oben angegebenen Ausdrücke für die Brennweiten der Flächen eingesetzt worden sind (Gleichungen (3) und (2); mit n=1 und n'=n ).

Die Lagen der Hauptebenen sind wie die Brennweiten Funktionen des Linsenmaterials ( n'/n ) und der Linsengeometrie (Radien der Grenzflächen und Dicke).

Mehrere und zusammengesetzte Linsen

Optische Systeme wie Mikroskope, Fernrohre und Objektive enthalten mehrere Linsen. Ihnen können als Einheit jeweils eine äquivalente Brennweiten und Hauptebenen zugeordnet werden. Die Berechnung von Brennweite und Hauptebenen kann unter der Annahme der paraxialen Näherung sehr effizient mittels der Matrizenoptik erfolgen.

Um Abbildungsfehler zu vermindern, werden häufig auch theoretisch als Einzellinsen denkbare Komponenten aus mehreren Linsen zusammengesetzt. Wenn zwei Berührungsflächen die gleiche Krümmung besitzen, können diese zwei Einzellinsen miteinander verkittet werden. Wenn die Einzellinsen dünn sind, ist auch der Abstand zwischen ihnen klein, so dass die Kombination selbst wie eine dünne Linse behandelt werden kann.

Abbildungsfehler

Abweichungen von der optischen Abbildung einer idealen Linse oder Linsensystems bewirken ein unscharfes oder verzerrtes Bild des abgebildeten Objektes.

Die wichtigsten Abbildungsfehler sind

die sphärische Aberration und die chromatische Aberration
der Astigmatismus und die Koma
die Linsendurchbiegung bei Linsengrößen über etwa 60 cm.
die Bildfeldwölbung und die Verzeichnung.

Die erstgenannten Fehler entstehen durch den üblicherweise kugelförmigen Linsenschliff und die Dispersion des Glases. Beide lassen sich durch Kombination zweier oder mehrerer Linsen reduzieren (siehe Achromat und Apochromat).

Hingegen erfordern Astigmatismus, Koma und Verzeichnungen kompliziertere Maßnahmen, wie asphärische Schliffformen, die Kombination mehrerer Linsengruppen (Anastigmat-Optiken, Weitwinkelobjektive) oder einfach die Beschränkung auf achsnahe Strahlen, durch Verringerung der Apertur oder ein kleineres Sichtfeld.

Oberflächenvergütung

Bei einer realen Linse wird immer ein Teil des Lichtes an der Oberfläche reflektiert. Bei einer Luft-Glas-Grenzfläche (Brechungsindex des Glases: n = 1,5) sind dies etwa 4 Prozent der einfallenden Intensität, d.h. bei einer Linse etwa 8 Prozent. In optischen Baugruppen, die aus mehreren Linsen aufgebaut sind, wie Objektiven, steigen die Verluste weiter fast linear an. So würden die Streuverluste eines fünflinsigen Objektivs auf 34 Prozent, die eines zehnlinsigen Objektivs auf 56 Prozent steigen.

Weiterhin kann mehrfach an den Grenzflächen reflektiertes Licht zusätzlich zum Nutzsignal aus dem System austreten und zu Verfälschungen der Abbildung führen. Um dieses zu vermeiden, werden die Linsenoberflächen in der Regel mit einer Antireflexbeschichtung versehen, man spricht auch von Oberflächenvergütung. Die Vermeidung bzw. Verringerung der beschriebenen Effekte wird dabei durch destruktive Interferenz der reflektierten Strahlen in den Antireflexionsschichten erreicht.

Besondere Linsentypen und Linseneffekte

Fourierlinse
Fresnellinse: Sie dient dem parallelen Ausrichten eines Lichtstrahls, etwa im Tageslichtprojektor oder im Leuchtturm. Auch Scheinwerfer nutzen ihr Prinzip. Lupen können ebenfalls als Fresnellinse ausgeführt werden.
Gaslinse: Die durch die Dichte beeinflusste optische Dichte von Gasen wird genutzt, um hochenergetische Laserstrahlung zu fokussieren. Hierzu wird das Licht durch ein rotierendes Rohr geleitet, in dem das mitbewegte Gas aufgrund des Bernoulli-Effekts Linseneigenschaften annimmt.
Diffraktive optische Elemente (DO-Glieder) werden vereinzelt in Objektiven für Spiegelreflexkameras eingesetzt.

Nicht nur transparente Bauelemente mit lichtbrechenden Oberflächen können Linseneffekte – also die Sammlung oder die Zerstreuung von Strahlung – erzeugen. So nutzen Elektronenmikroskope speziell angeordnete elektrische und magnetische Felder, um Elektronen zu fokussieren. Das Gleiche geschieht auch in Teilchenbeschleunigern in der Kern- und Hochenergiephysik. Von einer Gravitationslinse wird gesprochen, wenn durch ein massereiches astronomisches Objekt, wie etwa ein Schwarzes Loch, Linseneffekte hervorgerufen werden. Vereinzelt werden dadurch ferne Galaxien als Kreisbögen oder in mehrere Punkte verzerrt.

Literatur

Wolfgang Demtröder: Experimentalphysik. Band 2: Elektrizität und Optik. 2., überarbeitete und erweiterte Auflage. korrigierter Nachdruck. Springer, Berlin u.a. 2002, ISBN 3-540-65196-9.
Heinz Haferkorn: Optik. Physikalisch-technische Grundlagen und Anwendungen. 4., bearbeitete und erweiterte Auflage. Wiley-VCH, Weinheim 2003, ISBN 3-527-40372-8.
Eugene Hecht: Optik. 7. Auflage. De Gruyter, Berlin u.a. 2018, ISBN 978-3-11-052664-6.

Basierend auf einem Artikel in:

Wikipedia.de