Website durchsuchen

Potenzfunktion

Graphen einiger Potenzfunktionen

Als Potenzfunktionen bezeichnet man elementare mathematische Funktionen der Form

f\colon x\mapsto ax^{r}\qquad a,r\in \mathbb {R} .

Wenn man nur natürliche oder ganzzahlige Exponenten betrachtet, schreibt man für den Exponenten meistens n:

f\colon x\mapsto ax^{n}\qquad n\in \mathbb {Z} .

Ist der Exponent n eine natürliche Zahl, so ist der Funktionsterm ax^{n} ein Monom.

Spezialfälle

Definitions- und Wertemenge

Die maximal mögliche Definitionsmenge hängt vom Exponenten ab. Wenn man Wurzeln aus negativen Zahlen nicht zulässt, dann kann sie mit der folgenden Tabelle angegeben werden:

  r > 0 r < 0
r\in \mathbb {Z} \mathbb {R} \mathbb {R} \setminus \{0\}
r\notin \mathbb {Z} \mathbb {R} _{0}^{+} \mathbb {R} ^{+}

Bei den Wertemengen muss man zusätzlich noch das Vorzeichen von a beachten; wenn r\in \mathbb {Z} ist, kommt es außerdem auch noch darauf an, ob r eine gerade oder ungerade Zahl ist:

  r > 0 r < 0
  r gerade
oder \notin \mathbb {Z} 		r ungerade r gerade
oder \notin \mathbb {Z} 		r ungerade
a > 0 \mathbb {R} _{0}^{+} \mathbb {R} \mathbb {R} ^{+} \mathbb {R} \setminus \{0\}
a < 0 \mathbb {R} _{0}^{-} \mathbb {R} \mathbb {R} ^{-} \mathbb {R} \setminus \{0\}

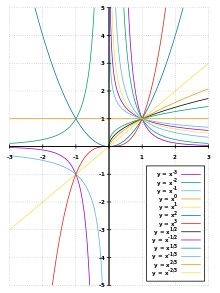
Graphen

Die Graphen der Potenzfunktionen mit natürlichen n heißen Parabeln n-ter Ordnung, die mit ganzzahligen negativen n Hyperbeln n-ter Ordnung. Der Parameter a drückt eine Streckung des Graphen bezüglich der y-Achse um den Faktor |a| und außerdem Spiegelung an der x-Achse aus, falls a<0 ist.

Hat eine Potenzfunktion die Definitionsmenge \mathbb {R} \setminus \{0\}, dann besteht ihr Graph aus zwei Ästen, ansonsten gibt es nur einen Ast.

Symmetrie

Nur die Graphen von Potenzfunktionen mit r\in \mathbb {Z} sind symmetrisch; genauer: sie sind gerade für gerade r und ungerade für ungerade r. Im ersten Fall ist ihr Graph achsensymmetrisch zur y-Achse, im zweiten ist er punktsymmetrisch zum Ursprung.

Verhalten für x → ±∞ und x → 0

Alle Potenzfunktionen x^{r} mit positiven Exponenten haben eine Nullstelle bei x=0, steigen (aber immer langsamer als die Exponentialfunktion e^{x}) und gehen gegen +\infty für x\to +\infty . Für r\in \mathbb {Z} ergibt sich das Verhalten für x\to -\infty aus der Symmetrie.

Alle Potenzfunktionen x^{r} mit negativen Exponenten gehen gegen +\infty für x\to 0\;(x>0). Sie fallen und gehen gegen {\displaystyle 0 } für x\to +\infty .

Stetigkeit, Ableitung und Integration

Jede Potenzfunktion f\colon x\mapsto ax^{r} ist stetig auf ihrer Definitionsmenge.

Die zugehörige Ableitungsfunktion ist (siehe Potenzregel)

f'\colon x\mapsto arx^{r-1}.

Diese Formel gilt für alle x\neq 0 und alle r, wenn x^{r} nur an der Stelle x definiert ist. Sie gilt auch an der Stelle x=0, wenn r\geq 1 ist. Für 0<r<1 ist die Funktion x\mapsto a\,x^{r} stetig, aber nicht differenzierbar an der Stelle x=0.

Zum Beispiel ist (x{\sqrt[{3}]{x^{2}}})'={\tfrac {5}{3}}{\sqrt[{3}]{x^{2}}} gültig in ganz \mathbb {R} _{0}^{+} (bzw. sogar in ganz \mathbb {R} wenn man ungerade Wurzeln aus negativen Zahlen zulässt – siehe unten).

Für eine beliebige nicht negative rationale Zahl {\displaystyle r\neq -1} ist die Formel

\int x^{r}\;dx={\frac {x^{r+1}}{r+1}}+C

für alle Intervalle, die Teilmengen der Definitionsmenge sind, gültig. Für r=-1 gilt

{\displaystyle \int x^{-1}\;dx=\int {\frac {1}{x}}\;dx=\ln(|x|)+C}

Zum Beispiel gilt:

\int x{\sqrt[{3}]{x^{2}}}\;dx=\int x^{5/3}\;dx=3/8~x^{8/3}+C=3/8~x^{2}{\sqrt[{3}]{x^{2}}}+C.

Potenzfunktionen mit Wurzeln aus negativen Zahlen

In diesem Abschnitt werden nur Potenzfunktionen mit rationalem Exponenten betrachtet, bei denen der Nenner des gekürzten Exponenten ungerade ist, und es wird erklärt, wie man deren Definitionsmenge auf negative Zahlen erweitern kann. Im Folgenden wird dann erläutert, welche der oben erwähnten Eigenschaften der Funktionen dadurch geändert werden.

Ungerade Wurzeln aus negativen Zahlen

(→ Siehe auch Potenz)

In den bisherigen Abschnitten wurde die in vielen Schulbüchern übliche Konvention verwendet, dass Wurzeln nur für nicht-negative Radikanden definiert sind. Man kann jedoch auch ungerade Wurzeln aus negativen Zahlen zulassen. Für ungerades n und beliebiges x\in \mathbb {R} definiert man, analog zur bekannten Definition für positive Radikanden:

{\sqrt[{n}]{x}} ist diejenige (eindeutige) reelle Zahl y, für die y^{n}=x gilt.

Beispielsweise wäre nach dieser Definition die Lösung der Gleichung x^{3}=-8 gegeben durch x={\sqrt[{3}]{-8}}=-2 (wohingegen man nach der üblichen Definition ohne Wurzeln aus negativen Zahlen x=-{\sqrt[{3}]{8}}=-2 schreiben müsste).

Definitions- und Wertemenge

Bei Potenzfunktionen mit den eingangs erwähnten Eigenschaften kann man nun den Definitionsbereich auf negative x erweitern : Sei r=n/m mit n\in \mathbb {Z} , m\in \mathbb {N} , m dabei ungerade, und seien m und n teilerfremd, dann gilt:

x^{r}={\sqrt[{m}]{x^{n}}} {\qquad } (oder, was äquivalent ist, {\quad } x^{r}=({\sqrt[{m}]{x}})^{n}).

(Anmerkung: Ist m=1, dann ergibt dies wieder eine Potenzfunktion mit einem ganzzahligen Exponenten.)

Für n>0 ist die Definitionsmenge dieser Funktion dann gleich \mathbb {R} , für n<0 ist sie gleich \mathbb {R} \setminus \{0\}.

Für die Wertemenge muss man wieder das Vorzeichen von a beachten. Außerdem kommt es nun auch noch darauf an, ob eine der Zahlen m oder n gerade ist (d.h. das Produkt mn gerade ist) oder ob diese beiden Zahlen ungerade sind (d.h. das Produkt mn ungerade ist):

  n > 0 n < 0
  mn gerade mn ungerade mn gerade mn ungerade
a > 0 \mathbb {R} _{0}^{+} \mathbb {R} \mathbb {R} ^{+} \mathbb {R} \setminus \{0\}
a < 0 \mathbb {R} _{0}^{-} \mathbb {R} \mathbb {R} ^{-} \mathbb {R} \setminus \{0\}

Symmetrie und Verhalten für x → ±∞ und x → 0

Für die Symmetrie gilt ähnliches wie bei ganzzahligen Exponenten: die Funktion ist gerade für gerade n und ungerade für ungerade n. Ihr Verhalten für x\to 0\;(x<0) und für x\to -\infty ist dann von ihren Symmetrieeigenschaften und von ihrem Verhalten auf der rechten Halbachse definiert.

Anwendungen

Potenzfunktionen haben vielfältige Anwendungen in Wirtschaft, Natur und Technik:

Literatur

Trenner
Basierend auf einem Artikel in: Wikipedia.de
Seitenende
Seite zurück
© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.09. 2022