Adiabatische Zustandsänderung

Eine adiabatische oder adiabate Zustandsänderung (griechisch α a, deutsch ‚nicht‘ und διαβαίνειν diabaínein ‚hindurchgehen‘) ist ein thermodynamischer Vorgang, bei dem ein System von einem Zustand in einen anderen überführt wird, ohne Wärme mit seiner Umgebung auszutauschen. In diesem Sinne werden adiabat und „wärmedicht“ synonym verwendet. Die Eigenschaft eines solchen Systems, keine Wärme mit der Umgebung auszutauschen, wird Adiabasie genannt. Im Gegensatz dazu wird bei diabatischen und diathermen Prozessen Wärme mit der Umgebung ausgetauscht (siehe etwa: Isotherme Zustandsänderung).

Adiabatische Zustandsänderungen, bei welchen vom Anfang bis zum Ende der Änderung zu jedem Zeitpunkt das System nahezu im Gleichgewicht ist, werden quasistatisch genannt, ihr Verlauf lässt sich durch eine Kurve im Zustandsraum darstellen. Wird die quasistatische Zustandsänderung allein durch die Veränderung von äußeren Parametern des Systems mittels idealisierter äußerer Vorrichtungen gesteuert, dann werden diese Kurven Adiabaten genannt. Äußere Parameter sind dabei Größen, die die äußeren, idealisierten Nebenbedingungen des thermodynamischen Systems beschreiben; wie etwa das Volumen des Systems oder die Komponenten der magnetischen Feldstärke eines äußeren Magnetfeldes.

Gedankenexperimente mit adiabatischen Zustandsänderungen sind grundlegend für die Ermittlung der Postulate der Thermodynamik. Sie liefern den Zusammenhang zwischen der an einem System geleisteten Arbeit und der inneren Energie des Systems. Der in der Literatur der Thermodynamik oft genutzte Carnotsche Kreisprozess beinhaltet die adiabatische Kompression und Expansion des Arbeitsgases. Bei dem axiomatischen Aufbau der Thermodynamik sind adiabatische Zustandsänderungen von zentraler Bedeutung. Die Bedingungen für adiabatische Zustandsänderungen werden in der Praxis nie ganz erreicht. Jedoch liefert diese Idealisierung für viele reale Vorgänge brauchbare bis gute Beschreibungen: etwa für schnell ablaufende Vorgänge, bei denen die Zeit für einen Temperaturausgleich nicht ausreicht, oder für Änderungen von Systemen in besonders wärmeisolierenden Behältern.

Geschichte

Der Begriff der adiabatischen Zustandsänderung entwickelte sich zusammen mit der Gas- und Wärmetheorie im 19. Jahrhundert.

Die Berechnung der Schallgeschwindigkeit in Luft regte Laplace und andere zu ersten Untersuchungen von adiabatischen Zustandsänderungen bei Gasen an. Im Jahre 1802 führte er eine zu klein berechnete Schallgeschwindigkeit darauf zurück, dass bei der schnellen Expansion und Kompression von Luft kein Temperaturausgleich stattfindet und das Gesetz von Boyle-Mariotte, $pV=const$ , hier nicht zutrifft. Im Jahre 1802 publizierte Biot und im Jahre 1808 Poisson Berechnungen zu Temperaturänderungen bei der adiabatischen Kompression in Schallwellen. In dieser Zeit wurden auch erste ausführliche Messungen der spezifischen Wärmekapazitäten von Gasen ausgeführt. Ch.B.Clement und N. Desormes publizierten 1819 für Luft erste Messwerte des Verhältnisses der Wärmekapazität bei konstantem Druck zu der bei konstantem Volumen, $c_{p}/c_{v}$ . Im Jahre 1823 berechnete Poisson mit diesem Wert und einer Theorie von Laplace die Schallgeschwindigkeit.

Im Jahre 1823 argumentierte Poisson mittels adiabatische Volumenänderungen für ein Verständnis von Wärme als einer Zustandsfunktion. 1824 benutzte Nicolas Léonard Sadi Carnot in seiner Arbeit Réflexions sur la puissance motrice du feu adiabatische Zustandsänderungen, um den Arbeitsstoff seiner idealen Wärmekraftmaschine zwischen den beiden Wärmereservoirs zu bewegen.

Im Jahre 1850 publizierte James Prescott Joule seine Messungen bei adiabatischen Zustandsänderungen mit Reibungsarbeit zur Bestimmung des Wärmeäquivalents.

Die Bezeichnung adiabatisch für Zustandsänderung ohne Wärmetransfer findet sich ab der zweiten Hälfte des 19. Jahrhunderts in der Literatur, so spricht Rankine in der Arbeit On the theory of explosive gas engines 1866 von adiabatic curves.

Der Mathematiker C. Carathéodory publizierte 1909 eine Arbeit über eine axiomatische Grundlegung der Thermodynamik. In dieser Arbeit haben adiabatische Zustandsänderungen in einfachen thermodynamischen Systemen eine zentrale Bedeutung. In einer neueren Arbeit zum zweiten Hauptsatz der Thermodynamik und der Entropie von 1999 nutzen Lieb und Yngvason adiabatische Zustandsänderungen zur Definition der Relation der Adiabatische Erreichbarkeit im thermodynamischen Zustandsraum.

Beispiele

Unter der in der Einleitung gegebenen Definition der adiabatischen Zustandsänderung fallen sehr viele Arten thermodynamischer Vorgänge, so auch solche die nicht quasistatisch verlaufen. Beim Lesen verschiedener Lehrbücher kann ein anderer Eindruck entstehen, da dort oft adiabatische Zustandsänderungen nur im Zusammenhang mit quasistatischen Vorgängen an einfachen Systemen betrachtet werden.

Nach Definition darf bei einer adiabatischen Zustandsänderung dem thermodynamischen System Energie nur mittels mechanischer, elektrischer oder magnetischer Arbeit zu- oder von ihm abgeführt werden, gegen Wärmeströme jeglicher Form muss das System isoliert sein; es darf im Idealfall keine Wärmeleitung, keine konvektive Wärmeübertragung und keine Wärmestrahlung zwischen dem System und der Außenwelt geben.

In der Realität ist eine vollständige Wärmeisolation nicht erreichbar, aber reale Vorgänge können in guter Näherung adiabatisch ablaufen, wenn

sie in einem gut isolierenden Behälter stattfinden, etwa in einem Dewargefäß oder einem adiabatischen Kalorimeter,
die Zustandsänderung so schnell verläuft, dass in der kurzen Zeit wenig Wärme zu- oder abfließen kann (z.B. in einem Verbrennungsmotor, bei einer Luftpumpe oder bei der Schallausbreitung) oder
das Volumen des Systems sehr groß ist, so dass Wärmeströme an seinem Rand praktisch keine Rolle spielen (z.B. bei thermisch aufsteigenden Luftpaketen).

Kompression und Expansion von Gasen

Die Kompression der Luft in einer Luftpumpe ist näherungsweise eine adiabatische Zustandsänderung. Die Arbeit, die an der Pumpe verrichtet wird, erhöht die innere Energie der Luft, und damit steigt auch die Temperatur der Luft. Bei schneller wiederholter Kompression, etwa beim Aufpumpen eines Fahrradreifens, ist die Temperaturerhöhung an der Pumpe gut fühlbar. Die zusätzliche innere Energie wird in der Umgangssprache auch Kompressionswärme oder Verdichtungswärme genannt.

Nebelbildung im Unterdruckbereich der Tragflächen eines Flugzeuges

Bei einem pneumatischen Feuerzeug wird Luft schnell auf weniger als ein Zwanzigstel ihres ursprünglichen Volumens komprimiert. Die Luft wird dabei so heiß, dass der eingelagerte Zunder erglimmt und damit dann ein Feuer entfacht werden kann.

Wird umgekehrt bei einer Ausdehnung eines Luftvolumens innere Energie in Volumenarbeit gewandelt, so fällt die Temperatur des expandierenden Gases. Bekannt ist die Abkühlung von Luftmassen beim thermischen Auftrieb oder beim Aufsteigen an Gebirgsrändern. Auch auf der Oberseite von Tragflächen von Verkehrsflugzeugen tritt eine adiabatische Expansion und damit eine Abkühlung der Luft auf, siehe Dynamischer Auftrieb. Die Abkühlung wird sichtbar, wenn die mit der Temperatur sinkende Sättigungskonzentration unter die vorhandene Luftfeuchtigkeit fällt und es zur Wolken- oder Nebelbildung kommt.

Auch bei dem Gay-Lussac-Versuch handelt es sich um eine adiabatische Zustandsänderung. Bei der Expansion des Gases wird allerdings keine innere Energie in äußere Arbeit umgewandelt. Der Vorgang verläuft nicht quasistatisch, nur am Anfang und Ende ist das System in einem thermodynamischen Gleichgewicht. Ideale Gase ändern dabei ihre Temperatur nicht.

Reibung

Es ist eine adiabatische Zustandsänderung, wenn an einem thermisch isolierten System Reibungsarbeit geleistet wird und sich das System zu Beginn und am Ende des Arbeitsprozesses im thermodynamischen Gleichgewicht befindet.

Joules Versuchsaufbau zur Bestimmung des Wärmeäquivalents

Die Versuchsdurchführung in dem klassischen Experiment zur Bestimmung des Wärmeäquivalents durch James Prescott Joule ist ein derartiger Prozess. Das System von Joule bestand aus einem Kupferbehälter mit Wasser und einem integrierten Rührwerk. Über das Rührwerk und einer Vorrichtung mit Gewichten wurde eine genau messbare mechanische Arbeit in innere Energie des Systems (vor allem Wasser) verwandelt. Joule hat die Temperatur vor und nach der Reibungsarbeit gemessen. In seinem Versuchsbericht von 1850 geht er auch auf seine Vorkehrungen zur thermischen Isolierung des Systems ein.

An Stelle einer definierten Menge mechanischer Arbeit kann auch eine gemessene Menge elektrischer Arbeit $\int U(t)I(t)dt$ an einem System geleistet werden, um etwa die Wärmekapazität einer Substanz zu bestimmen. Das Rührwerk wird dabei durch eine elektrische Heizung ersetzt; das thermodynamische System besteht aus einem Behälter, der Substanz und der Heizung. Zur thermischen Isolation befindet sich das System am besten in einem Dewargefäß oder einem adiabatischen Kalorimeter. Wenn sich vor und nach dem Einbringen der elektrischen Energie das System im thermodynamischen Gleichgewicht befindet, handelt es sich um eine adiabatische Zustandsänderung.

Elektrochemische Zelle

Ein Akkumulator als thermodynamisches System kann Energie in Form von elektrischer Arbeit nach außen abgeben oder ihm kann Energie mittels elektrische Arbeit von außen zugeführt werden, je nach Stromrichtung in den elektrischen Zuleitungen. Die Zuführung oder Entnahme elektrischer Energie führt zu einer Änderung der Stoffmengen an den Elektroden. Wenn dabei der Akkumulator durch ein adiabatisches Kalorimeter thermisch isoliert ist, handelt es sich um adiabatische Zustandsänderungen. Da bei dem Vorgang immer ohmsche Verluste auftreten, erwärmt sich das System mehr oder weniger stark. Schon wegen dieser ohmschen Verluste ist die Zustandsänderung nicht reversibel. Solche adiabatische Zustandsänderungen werden etwa bei Sicherheitsprüfungen von Batterien herbeigeführt und vermessen.

Zusammenführung von Systemen

In der Thermodynamik werden häufig adiabatische Zustandsänderungen betrachtet, bei welchen der Anfangszustand aus zwei Systemen besteht, die jeweils für sich im thermodynamischen Gleichgewicht sind. Die beiden Systeme werden als ein einziges zusammengesetztes System betrachtet. Die Zustandsänderung erfolgt, in dem die Systeme ohne Arbeitsaufwand miteinander verbunden werden und dann miteinander wechselwirken; etwa durch einen thermischen Kontakt oder durch Herausnahme einer Trennwand zwischen den Systemen – z.B. Öffnen eines Trennventils. Die dabei ablaufenden Vorgänge sind irreversibel und können sehr heftig verlaufen. Die Änderung ist abgeschlossen, wenn das gesamte System sich nach der Kopplung nicht mehr ändert, also zu einem neuen thermodynamischen Gleichgewicht gefunden hat.

Dewargefäß
(Deutsches Museum, München)

Damit die Zustandsänderung adiabatisch ist muss das zusammengesetzte System von der Umgebung thermisch isoliert sein, hierfür eignen sich Dewargefäße oder adiabatische Kalorimeter. Es folgen einige Beispiele für solche Zustandsänderungen:

Lösungswärme-Bestimmung: Ein System bestehe aus einer bekannten Stoffmenge Wasser und das andere aus einer bekannten Stoffmenge Kochsalz. Beide Systeme haben Zimmertemperatur. Dann wird das Salz in das Wasser gegeben – Kopplung der Systeme. Es löst sich in dem Wasser auf, anschließend wird die Temperatur der Salzlösung gemessen.
Neutralisationswärme-Bestimmung: Ein System sei eine Säure und das andere eine Lauge. Dann werden Säure und Lauge vorsichtig zusammengerührt und die Temperatur der Mischung verfolgt, bis sie sich nicht mehr ändert. Aus der Temperaturänderung und den Stoffmengen, kann die Neutralisationswärme bestimmt werden.
Chemische Reaktion: Am Anfang sei ein System von zwei mol Wasserstoff und ein System mit ein mol Sauerstoff gegeben. Wird ein Trennventil zwischen den beiden Systemen geöffnet, entsteht eine Knallgasmischung, die schließlich zu Wasser reagiert. Im Endzustand besteht das System aus Wasser.
Phasen im Gleichgewicht: Ein System sei Wasser in der flüssigen Phase, das Zweite Wasserdampf in einem Behälter. Nach einer Verbindung der beiden Systeme stellt sich ein Gleichgewicht, zwischen der flüssigen und der gasförmigen Phase ein.

Wärmeausgleich zwischen zwei Systemen

Seien A und B zwei einfache Systeme, bei Prozessbeginn getrennt und jeweils im thermischen Gleichgewicht. A habe eine höhere Temperatur als B.

Irreversibler Wärmeausgleich: Werden die Systeme zusammengeschoben, so dass sie sich berühren, oder werden sie über einen Kupferdraht miteinander thermisch verbunden, fließt Wärme irreversibel vom System A zum System B, bis beide Systeme die gleiche Endtemperatur haben.
Reversibler Wärmeausgleich: Wird die Wärmeenergie von dem wärmeren zu dem kälteren System durch eine ideale Wärmekraftmaschine – Carnot-Prozess – transportiert, nähern sich die Temperaturen der Systeme an. Dabei wird zusätzlich zu der Wärmeübertragung von dem Gesamtsystem eine Arbeit geleistet, ihm also Energie entzogen. Wird dieser Prozess solange wiederholt, bis die Temperaturen der beiden Systeme gleich sind, so ist die Endtemperatur niedriger als beim irreversiblen Wärmeaustausch, da die Energie des Gesamtsystems abgenommen hat, die Entropie aber gleich geblieben ist. Umgekehrt kann die Temperaturdifferenz zwischen den Systemen A und B auch wieder vergrößert werden, wenn unter Zuführung äußerer Arbeit die Maschine zwischen den Systemen als Wärmepumpe betrieben wird.

Theorie

Eine adiabatische Zustandsänderung ist eine Änderung eines bis auf Arbeitsprozesse isolierten thermodynamischen Systems von einem Gleichgewichtszustand $z_{1}$ zu einem Gleichgewichtszustand $z_{2}$ ; an dem System kann von außen eine mechanische oder elektrische Arbeit verrichtet werden oder es kann eine solche Arbeit leisten. Wird durch die Arbeit dem System Energie zugeführt, dann ist $W>0$ ; leistet das System Arbeit, dann ist $W<0$ ; wird keine Arbeit verrichtet, so ist $W=0$ . Für den Aufbau der Thermodynamik ist es wichtig: dass diese Definition der adiabatische Zustandsänderung ohne den Begriff Wärme auskommt.

Adiabatische Erreichbarkeit

Ein Zustand $z_{2}$ eines thermodynamischen Systems wird als von dem Zustand $z_{1}$ adiabatisch erreichbar bezeichnet, wenn es eine adiabatische Zustandsänderung gibt, welche $z_{1}$ als Anfangs- und $z_{2}$ als Endzustand hat.

Für ein thermodynamisches System gelten die beiden Postulate:

Für je zwei Gleichgewichtszustände $z_{1}$ und $z_{2}$ gilt: $z_{2}$ ist von $z_{1}$ adiabatisch erreichbar oder $z_{1}$ von $z_{2}$ .
Gibt es zwei adiabatische Zustandsänderungen mit dem gleichen Anfangszustand $z_{1}$ und dem gleichen Endzustand $z_{2}$ , dann ist die Arbeit $W_{1}$ der einen Zustandsänderung gleich der Arbeit der anderen.

Für zwei Zustände $z_{1}$ und $z_{2}$ kann es sein, dass sowohl $z_{2}$ von $z_{1}$ mit einer Arbeit $W_{1}$ adiabatisch erreichbar ist, als auch $z_{1}$ von $z_{2}$ mit einer Arbeit W_2 adiabatisch erreichbar ist, dann gilt $W_{2}=-W_{1}$ .

Definition der inneren Energie

Aufgrund dieser Postulate ist es möglich, die innere Energie als Zustandsfunktion für ein thermodynamisches System einzuführen. Für einen beliebigen Gleichgewichtszustand $z_{0}$ wird ein Wert $U(z_{0})$ willkürlich festgesetzt. Die innere Energie für einen beliebigen Zustand ergibt sich dann wie folgt:

ist von $z_{0}$ durch eine adiabatische Zustandsänderung mit einer Arbeit erreichbar, dann gilt $U(z)=U(z_{0})+W$ .
andernfalls muss $z_{0}$ von durch eine adiabatische Zustandsänderung mit einer Arbeit erreichbar sein und es ist $U(z)=U(z_{0})-W$ .

Die Wärmemenge als physikalische Größe

Die innere Energie ist nur bis auf eine Konstante festgelegt. Mit ihr wird für eine allgemeine Zustandsänderung eines thermisch nicht isolierten Systems von einem Anfangszustand $z_{a}$ zu einem Endzustand $z_{b}$ und einer Arbeit die dabei dem System zugeführte Wärme durch

$Q=U(z_{b})-U(z_{a})-W$

definiert. Für eine adiabatische Zustandsänderung folgt Q=0 .

Adiabatische Zustandsänderungen werden nicht nur gebraucht, um – wie gerade gezeigt – die innere Energie und die Wärme als physikalische Größen zu definieren, sie können auch im Rahmen eines axiomatischen Aufbaus der Thermodynamik dazu dienen, die Temperatur und die Entropie einzuführen. Hier sind zwei Ansätze erwähnenswert:

Axiomatische Modelle

Schematische Darstellung des Zustandsraumes eines einfachen thermodynamischen Systems – dicke Linien zeigen Hyperflächen mit konstanter Entropie, der Pfeil zeigt die Richtung zunehmender Entropie – Der Zustand $z_{2}$ ist von $z_{1}$ adiabatisch erreichbar aber nicht $z_{1}$ von $z_{2}$ . – Sowohl $z_{3}$ ist von $z_{2}$ adiabatisch erreichbar als auch umgekehrt $z_{2}$ von $z_{3}$ .

Der Mathematiker Constantin Carathéodory setzt in seiner Untersuchung über die Grundlagen der Thermodynamik die Aussage:

„In jeder beliebigen Umgebung eines willkürlich vorgeschriebenen Anfangszustandes gibt es Zustände, die durch adiabatische Zustandsänderungen nicht beliebig approximiert werden können.“

als ein Axiom an den Anfang eines mathematischen Modells für thermodynamische Systeme. Dieses Axiom ist dem zweiten Hauptsatz der Thermodynamik äquivalent.

Carathéodory führt in seiner Arbeit den Begriff des einfachen thermodynamischen Systems ein: es ist ein System, bei dem jeder Gleichgewichtszustand allein durch die Angabe eines Wertes für die innere Energie und eines Tupel äußerer Parameter $V_{1},\dots ,V_{m}$ für die äußeren Nebenbedingungen eindeutig festgelegt ist.

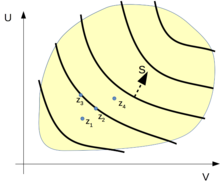
Elliot H. Lieb und Jakob Yngvason entwickeln in einer neueren Arbeit zum zweiten Hauptsatz der Thermodynamik ein mathematisches Modell für thermodynamische Systeme ohne die bei Caratheodory gemachten impliziten Annahmen über analytische Eigenschaften der Zustandsfunktionen. Dieses Modell baut auf der durch die adiabatische Erreichbarkeit gegebene Quasiordnung im Zustandsraum auf; siehe hierzu auch die nebenstehende schematische Zeichnung. Eine Darstellung in Deutsch mit anschaulichen Anwendungsbeispielen findet sich in einem Lehrbuch von André Thess.

Mit ergänzenden Axiomen zur Skalierung und Kopplung thermodynamischer Systeme definieren Lieb und Yngvason für Gleichgewichtszustände die Zustandsfunktion der Entropie und hierüber erst die Temperatur. Für die Entropie S(z) gilt die Monotonie: In einem einfachen thermodynamischen System ist ein Gleichgewichtszustand $z_{2}$ von einem Zustand $z_{1}$ adiabatisch erreichbar, genau dann wenn $S(z_{2})\geq S(z_{1})$ .

Adiabaten

Eine adiabatische Zustandsänderung wird quasistatisch genannt, wenn sich das System bei der Änderung zu jedem Zeitpunkt nahezu im thermodynamischen Gleichgewicht befindet. In diesem Fall beschreiben die bei der Änderung eingenommenen Gleichgewichtspunkte einen zusammenhängenden Weg im Zustandsraum $\Gamma$ . Dieser Weg wird Adiabate genannt, wenn die quasistatische Zustandsänderung allein durch die Veränderung von äußeren Parametern des Systems mittels idealisierter äußerer Vorrichtungen gesteuert wird. Äußere Parameter sind dabei Größen, die die äußeren, idealisierten Nebenbedingungen des thermodynamischen Systems beschreiben; wie etwa das Volumen des Systems oder die Komponenten der magnetischen Feldstärke eines äußeren Magnetfeldes. Der Verlauf von Zustandsänderungen bei Prozessen mit Reibungsarbeit wird dagegen nicht als Adiabate bezeichnet.

Können die äußeren Nebenbedingungen eines Systems durch äußere Parameter $\alpha _{1},...,\alpha _{n}$ beschrieben werden, dann gibt es zu jedem äußeren Parameter $\alpha _{i}$ eine Funktion $\beta _{i}(z)$ , so dass bei einer adiabatischen Zustandsänderung längs einer Adiabaten die an dem System geleistete Arbeit gleich dem Wegintegral über eine 1-Form ist.

$W=U(z_{2})-U(z_{1})=\int _{z_{1}}^{z_{2}}\sum _{i=1}^{n}\beta _{i}(z)d\alpha _{i}$

Einfache thermodynamischen Systeme sind solche Systeme, bei welchen die äußeren Parametern zusammen mit der inneren Energie einen Gleichgewichtszustand eindeutig bestimmt; die Größen $U,\alpha _{1},...,\alpha _{n}$ bilden dann ein Koordinatensystem in $\Gamma$ . Beispiele für nicht einfache thermodynamische Systeme sind das Gesamtsystem aus zwei von einander isolierten, einfachen Systemen oder wegen der Hysterese ein System mit ferromagnetischem Material.

Bei einfachen thermodynamischen Systemen sind die quasistatischen adiabatischen Zustandsänderungen immer reversibel. Damit sind die Adiabaten bei einfachen thermodynamischen Systemen auch zugleich Kurven konstanter Entropie; bei diesen Systemen sind die Adiabaten identisch mit den Isentropen. Wegen der großen praktischen Bedeutung dieser einfachen Systeme wird Adiabate und Isentrope in der Literatur oft synonym gebraucht. Dieses kann allerdings verwirren, da bei nicht einfachen thermodynamischen Systemen Adiabate und Isentrope verschieden sein können. Außerdem setzt die Einführung der Entropie in der Thermodynamik den Begriff der adiabatischen Zustandsänderung bereits voraus.

Adiabaten des idealen Gases

Die Gleichgewichtszustände des einfachen thermodynamischen Systems bestehend aus einer festen Stoffmenge eines Gases in einem Behälter mit dem veränderbaren Volumen bilden einen zweidimensionalen Zustandsraum $\Gamma$ . Werden die Temperatur des Gases und das Volumen als Koordinaten für die Punkte in $\Gamma$ gewählt, so ergibt sich für die durch eine Änderung des Volumens um an dem System geleistete Arbeit:^{[A
1]}

$\delta W=-p(T,V)dV=-{\frac {nRT}{V}}dV$

Die letzte Gleichheit gilt nur für ein ideales Gas, bei ihm ist der Druck $p(T,V)$ durch die Zustandsfunktion des idealen Gases $p(T,V)=(nRT)/V$ gegeben, mit als Stoffmenge und der Gaskonstanten. Weiter ist bei einem idealen Gas die Änderung der inneren Energie unabhängig vom Volumen und proportional der Temperaturänderung.

$dU=nc_{v}dT$

$c_{v}$ ist die konstante molare Wärmekapazität bei konstantem Volumen.

Bei adiabatischen Prozessen gilt

$dU=\delta W\quad$ und damit für das ideale Gas $\quad nc_{v}dT+{\frac {nRT}{V}}dV=0\quad$

Diese Gleichung ist genau dann erfüllt wenn

$TV^{\frac {R}{c_{v}}}={\text{konstant}}$

gilt; das bedeutet: ist das System am Anfang einer adiabatischen Zustandsänderung an dem Punkt $(T_{1},V_{1})$ und am Ende sei das Volumen V_2 , dann errechnet sich die Endtemperatur $T_{2}$ zu:

$T_{2}=T_{1}\left({\frac {V_{1}}{V_{2}}}\right)^{\frac {R}{c_{v}}}=T_{1}\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma -1}$

Adiabate und Isotherme für ein ideales einatomiges Gas

In der letzten Gleichung wurde der Exponent $R/c_{v}$ durch den hier häufig gebrauchten Adiabatenexponenten $\gamma =c_{p}/c_{v}$ mit $c_{p}=c_{v}+R$ ausgedrückt, für Luft ist $\gamma =1{,}4$ . Werden die Punkte in $\Gamma$ durch die Koordinaten $(p,V)$ oder $(T,p)$ beschrieben, so lautet die Gleichung

$\quad p_{2}=p_{1}\left({\frac {V_{1}}{V_{2}}}\right)^{\gamma }$ bzw. $\quad T_{2}=T_{1}\left({\frac {p_{1}}{p_{2}}}\right)^{\frac {1-\gamma }{\gamma }}$

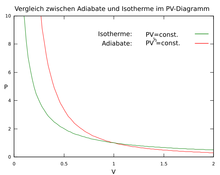
Sie folgen aus der ersten Beziehung unter Ausnutzung der Zustandsgleichung für ideale Gase. Diese Gleichungen werden Adiabatengleichungen oder Poissongleichungen genannt. Jede ist jeweils eine Bedingungsgleichung für die Adiabate eines idealen Gases in dem $(T,V)$ -, $(p,V)$ - bzw. $(T,p)$ -Diagramm.

Numerische Beispiele für Luft

Beim lokalen Druckwechsel im Zuge der Schallausbreitung in Luft, bei dem Aufstieg großer Luftmassen in der Atmosphäre, bei Wärmekraftmaschinen (siehe hierzu auch Verdichtungsverhältnis) oder bei einer Luftpumpe gibt es Expansionen oder Kompressionen von Luftmassen, die sich oft in guter Näherung als adiabatische Zustandsänderungen beschreiben lassen.

Aus den Anfangswerten $V_{1},p_{1},T_{1}$ , dem Kompressionverhältnis und dem Adiabatenexponenten $\gamma =1{,}4$ können die Endwerte $p_{2},T_{2}$ bzw. $V_{2},T_{2}$ für eine solche Zustandsänderung berechnet werden. Für einige Beispielwerte von $V_{2}/V_{1}$ finden sich nach der obigen Adiabatengleichung berechnete Werte in der folgenden Tabelle.

Vorgang	${\frac {V_{2}}{V_{1}}}$	${\frac {p_{2}}{p_{1}}}$	${\frac {T_{2}}{T_{1}}}$	$(T_{2}-T_{1})/\mathrm {K}$ bei $T_{1}=293{,}15\,\mathrm {K}$
Fälle adiabatischer Kompression
Schall von einem sprechenden Menschen in 1 m Abstand	$0{,}99999985$	$1{,}00000020$	$1{,}00000010$	$0{,}0003$
Volumenreduktion um 10 %		$1{,}16$	$1{,}04$	$12{,}6$
Volumenreduktion um 50 %		$2{,}64$	$1{,}32$	$93{,}7$
Fahrradpumpe von 1 auf 5 bar absolut, also 4 bar Überdruck	$0{,}316$		$1{,}584$	$171{,}2$
Ottomotor (Verdichtung 1:10)		$25{,}11$	$2{,}51$	$443{,}2$
Dieselmotor (Verdichtung 1:20)	$0{,}05$	$66{,}29$	$3{,}31$	$678{,}5$
(Hochdruckkompressor füllt eine Tauchflasche von 1 bar Umgebungsdruck auf 199 bar Überdruck)	$0{,}0227$	$200$	$4{,}543$	$1038{,}9$
Verdichtung 1:100 (noch extremere Verdichtung gibt es z.B. beim Wiedereintritt)		$631$	$6{,}31$	$1556{,}5$
Fälle adiabatischer Expansion
Aufstieg trockener Luft um ca. 100 m in der unteren Erdatmosphäre	$1{,}01$	$0{,}986$	$0{,}996$	$-1{,}16$
Aufstieg trockener Luft um ca. 1000 m in der unteren Erdatmosphäre		$0{,}88$	$0{,}96$	$-10{,}96$
–		$0{,}38$	$0{,}76$	$-71{,}0$
Ausströmen von Pressluft, Druckminderung von 10 bar auf 1 bar	$5{,}18$		$0{,}518$	$-141{,}3$
–		$0{,}039$	$0{,}40$	$-176{,}4$
(Ausströmen von Pressluft, Druckminderung von 200 bar auf 1 bar)	$44{,}014$	$0{,}005$	$0{,}220$	$-228{,}6$

Die ermittelte Temperaturveränderung der absoluten Temperatur $T_{2}-T_{1}$ (in Kelvin oder zugleich °Celsius) in der letzten Spalte gelten für eine Ausgangstemperatur $T_{1}=293{,}15\,\mathrm {K}$ (= 20 °C) am Anfang des Vorgangs.

Die hier berechneten Werte gelten für idealisierte Luft, also unter folgenden Annahmen:

ideales Gas, also
- geringer Druck (< 100 bar) (Fälle mit höherem Druck sind eingeklammert) und
- ausreichend hohe Temperatur (> 200 K)
eine temperaturunabhängige molare Wärmekapazität $c_{v}$ , tatsächlich nimmt diese bei Stickstoff und Sauerstoff langsam mit der Temperatur zu.
zweiatomige Moleküle wie Stickstoff N₂, Sauerstoff O₂ (1- und 3-atomige Moleküle haben abweichende Adiabatenexponenten $\gamma$ ); nur bei Edelgasen ist der Adiabatenexponent konstant, bei mehratomigen Molekülen fällt er langsam mit zunehmender Temperatur.
trockene Luft, also frei von Wasserdampf (enthält Luft Wasserdampf kann Kondensation auftreten, sowohl bei Druckerhöhung als auch durch Temperaturabsenkung unter den Taupunkt)
Die Wände des Behälters bewegen sich mit Geschwindigkeiten, die kleiner als die mittlere thermische Geschwindigkeit der Moleküle sind. Als praktische Grenzgeschwindigkeit kann die Schallgeschwindigkeit angesehen werden, da diese von der Größenordnung der thermischen Geschwindigkeiten ist.

Mikroskopische Betrachtung

Eine adiabatische Zustandsänderung lässt sich makroskopisch an einem Systems aus vielen Teilchen betrachten und beschreiben. Die Änderungen im mikroskopischen Bereich lassen sich an folgendem Beispiel nachvollziehen, wobei ein adiabater Zylinder angenommen wird, in dem ein ideales, stark verdünntes Gas bei Umgebungstemperatur von einem Kolben im Laufe einer Zustandsänderung auf das halbe Volumen komprimiert wird. Daraus resultiert eine Druckerhöhung und eine Temperaturerhöhung, die sich so erklären lassen:

Der Druck entsteht dadurch, dass die Gasteilchen (Atome bei Edelgasen, Moleküle bei anderen idealen Gasen) sich sehr schnell bewegen und regelmäßig mit der Wand des Zylinders oder dem Kolben zusammenstoßen und wieder abprallen.
Halbiert man das Volumen, so halbiert sich die Strecke für die Gasteilchen zwischen den Zylinderwänden und dem Kolben. Da gleiche Anzahl von Teilchen nun bei halbiertem Weg doppelt so oft auf den Kolben prallen, verdoppelt sich der makroskopisch messbare Druck. Diese Druckzunahme lässt sich aus der allgemeinen Gasgleichung berechnen und entspricht der Druckerhöhung bei einer isothermen Kompression, d.h. diese Druckerhöhung bleibt auch erhalten, wenn man nach einer adiabatischen Kompression das Gas auf Umgebungstemperatur abkühlen lässt.
Während der Kolben das Volumen komprimiert, bewegt er sich. Die Gasteilchen, die dann auf den Kolben prallen, erhalten beim Rückprall eine höhere Geschwindigkeit. Dieser Anteil der zugeführten Energie erhöht die Temperatur des Gases im Kolben. Die Bewegungsgeschwindigkeit des Kolbens ist bei einem wärmedichten Zylinder (bei einer adiabaten Kompression vorausgesetzt) für die Temperaturzunahme unerheblich. Bei langsamer Bewegung finden viele Teilchenstöße mit geringer Geschwindigkeitszunahme statt oder bei schneller Bewegung finden wenige Stöße mit großer Geschwindigkeitszunahme statt.

Dadurch, dass die Gasteilchen auch untereinander zusammenstoßen und Impuls austauschen, zeigt sich die Druckerhöhung nicht nur am Kolben, sondern an der gesamten Innenwand des Zylinders.

Siehe auch

Literatur

Günther Ludwig: Einführung in die Grundlagen der theoretischen Physik. Band 4. Vieweg & Sohn, Braunschweig 1979, ISBN 3-528-09184-3.

Anmerkungen

↑ Die geleistete Arbeit ist hier als Differentialform geschrieben, eine reale Arbeit ergibt sich als ein Integral dieser Ein-Form über den Prozessweg. Da die Differentialform für die verrichtete Arbeit sich im Allgemeinen nicht als totales Differential einer Zustandsfunktion schreiben lässt, wird hier statt des Symbols $dW$ das Symbol $\delta W$ benutzt.

Basierend auf einem Artikel in:

Wikipedia.de