Isentrop

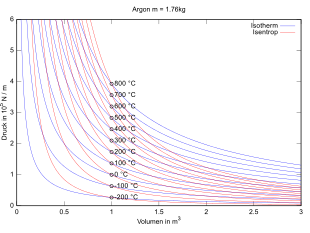
isentrope und isotherme Zustandsänderung
im p-V-Diagramm

In der Thermodynamik wird ein Prozess bzw. eine Strömung als isentrop bezeichnet, wenn sich die Entropie nicht ändert:

$\begin{align} S & = konst.\\ \Leftrightarrow \frac{\mathrm{d}S}{\mathrm{d}t} & = 0 \end{align}$

Als Isentrope bezeichnet man Linien gleicher Entropie. Da Entropie und potentielle Temperatur direkt miteinander in Beziehung stehen, wird der Begriff der Isentrope auch synonym für Linien gleicher potentieller Temperatur gebraucht.

Ein adiabatisch reversibler Prozess ist immer auch isentrop, die Umkehrung gilt aber nicht.

Die isentrope Zustandsänderung idealer Gase lässt sich durch die Poissonschen Gleichungen beschreiben:

$p(v) = p_0 \cdot {\left(\frac{v_0}{v}\right)^{\kappa}}$

$T(v) = T_0 \cdot {\left(\frac{v_0}{v}\right)^{\kappa-1}}$

$T(p) = T_0 \cdot {\left(\frac{p}{p_0}\right)^\frac{\kappa-1}{\kappa}}$

dabei sind:

Der Index 0 kennzeichnet den Ausgangszustand, die Größen ohne Index sind die Variablen.

Basierend auf einem Artikel in:

Wikipedia.de