Geometrischer Schwerpunkt

Der geometrische Schwerpunkt oder Schwerpunkt einer geometrischen Figur (zum Beispiel Kreisbogen, Dreieck, Kegel) ist ein besonders ausgezeichneter Punkt, den man auch bei unsymmetrischen Figuren als Art Mittelpunkt interpretiert. Mathematisch entspricht dies der Mittelung aller Punkte innerhalb der Figur. Im Speziellen wird der geometrische Schwerpunkt von Linien auch Linienschwerpunkt, von Flächen Flächenschwerpunkt und von Körpern Volumenschwerpunkt genannt. Den Schwerpunkt kann man in einfachen Fällen durch geometrische Überlegungen erhalten, oder allgemein mit Mitteln der Mathematik durch Integration berechnen. Zur Beschreibung der Körper werden die Methoden der analytischen Geometrie verwendet. Der Schwerpunkt ist ein Gravizentrum.

Der geometrische Schwerpunkt entspricht dem Massenmittelpunkt eines physikalischen Körpers, der aus homogenem Material besteht, also überall die gleiche Dichte hat. Er lässt sich deshalb auch rein mechanisch durch Balancieren bestimmen. Diese Methode kann an Modellen angewandt werden, wenn es um geografische Mittelpunkte von Kontinenten oder Ländern geht (zum Beispiel Mittelpunkt Europas oder Mittelpunkt Deutschlands).

Schwerpunkte von elementargeometrischen Figuren

Im Folgenden werden einige Schwerpunkte elementargeometrischer Linien, Flächen und Körper angegeben und teilweise durch geometrische Überlegungen begründet.

Für achsensymmetrische oder rotationssymmetrische Figuren vereinfacht sich die Angabe des Schwerpunkts dadurch, dass dieser stets auf der Symmetrieachse liegt. Bei Figuren mit mehreren Symmetrieachsen bzw. punktsymmetrischen Objekten, wie beispielsweise bei einem Quadrat oder einem Kreis, liegt der Schwerpunkt im Schnittpunkt der Symmetrieachsen (Mittelpunkt) der Figur.

Linien

Gerade Linie

Der Schwerpunkt einer geraden Linie der Länge liegt in ihrer Mitte:

$x_S=\frac l 2$

Kreisbogen

Schwerpunkt eines Kreisbogens

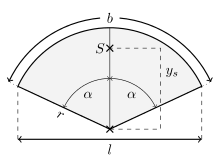
Ist der Ausschnitt des Kreises so gedreht und verschoben, dass die y-Achse des kartesischen Koordinatensystems eine Symmetrieachse des Kreisbogens ist und der Mittelpunkt des Kreises im Koordinatenursprung liegt (siehe Bild), dann lässt sich der Schwerpunkt durch

$x_s = 0 \quad y_s=\frac{2 r^2 \sin\alpha}{b}=r \frac{l}{b}$

berechnen. Hierbei ist der Radius des Kreises, die Länge des Kreisbogens und die Sehnenlänge des Kreisbogens.

$0 < \alpha \le \pi$

Für $\alpha =0$ versagt die Formel. Mit $\lim_{\alpha \to 0}{\tfrac l b} = \cos\alpha$ kann der Schwerpunkt auch für sehr kleine Winkel berechnet werden.

Musste der Kreis zu anfangs verschoben oder gedreht werden, dann muss zur Vervollständigung der Rechnung der berechnete Schwerpunkt entsprechend wieder zurückverschoben oder gedreht werden.

Flacher Bogen

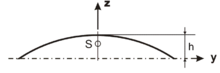
Um den Schwerpunkt eines flachen Bogens näherungsweise zu berechnen, muss dieser im kartesischen Koordinatensystem so verschoben werden, dass der Mittelpunkt der Verbindungslinie der beiden Endpunkte im Koordinatenursprung liegt. Dann befindet sich der Schwerpunkt für h<r in guter Näherung etwas unterhalb von

$z_s\approx\frac{2h}3$ .

Bei h=r (Halbkreis) liegt der Schwerpunkt exakt bei $\frac{2r}{\pi}$ . Die prozentuale Abweichung steigt in etwa proportional mit h und beträgt bei h=r ungefähr 4,7 %. Daraus folgt der Ausdruck $\frac{2000h}{3(1000+47h/r)}$ , der den Schwerpunkt im Bereich von $(0\leq h\leq r)$ mit einer Genauigkeit von besser als 5 Promille angibt. Die exakte Lage des Linienschwerpunktes z_s(h) im gesamten Bereich von $(0< h\leq 2r)$ findet man mittels Einsetzen von $\alpha=\arccos(1-h/r)$ in die Formel für den auf den Kreismittelpunkt bezogenen Schwerpunkt $r \sin(\alpha)/\alpha$ (siehe Kreisbogen):

$z_s=h-r+\frac{\sqrt{r^2-(h-r)^2}}{\arccos (1-h/r)}$ .

Interessanterweise zeigt z_s ein Maximum etwas größer als bei $h\approx 1,9r$ . War zu Beginn eine Verschiebung oder Drehung notwendig, so muss der Schwerpunkt wieder entsprechend zurückverschoben werden.

Ebene Flächen

Bei ebenen Flächen lässt sich der Schwerpunkt allgemein dadurch ermitteln, dass man die ausgeschnittene Fläche an einem Punkt aufhängt und die Lotgerade, eine so genannte Schwerelinie einzeichnet. Der Schnittpunkt zweier Schwerelinien ist der Schwerpunkt. Alle weiteren Schwerelinien schneiden sich ebenfalls in diesem Schwerpunkt.

Dreieck

Schwerpunkt eines Dreiecks

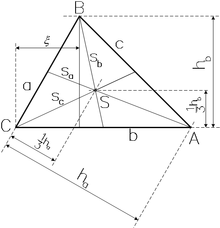
Die Seitenhalbierenden eines Dreiecks sind Schwerelinien des Dreiecks. Sein Schwerpunkt liegt im gemeinsamen Schnittpunkt der drei Seitenhalbierenden. Er teilt diese im Verhältnis 2:1, wobei die längere der beiden Teilstrecken die Strecke vom Schwerpunkt zum Eckpunkt ist.

Sind die kartesischen Koordinaten der Eckpunkte des Dreiecks bekannt, so ergibt sich der Schwerpunkt S = (x_s,y_s) als arithmetisches Mittel.

$x_s = \frac13 (x_A+x_B+x_C),\quad y_s = \frac13(y_A+y_B+y_C)$

Seine baryzentrischen Koordinaten sind daher $(\tfrac13,\tfrac13,\tfrac13)$ .

Ausgedrückt durch trilineare Koordinaten lautet der Schwerpunkt eines Dreiecks mit Seitenlängen , ,

$\left(\frac{1}{a}, \frac{1}{b}, \frac{1}{c} \right) = (bc, ca, ab)\,.$

Man kann den Schwerpunkt auch mit Hilfe der Länge einer Seite und der Höhe $h_{b}$ über der gleichen Seite in kartesischen Koordinaten bestimmen. Der Ursprung des Koordinatensystems liegt im Eckpunkt (siehe Abbildung). Auf diese Weise lassen sich die kartesischen Koordinaten des Schwerpunkts durch

$x_s = \frac{b+\xi}{3},\quad y_s = \frac{h_b}{3}$

berechnen.

Der Schwerpunkt eines Dreiecks ist Mittelpunkt der Steiner-Ellipse (Steiner-Umellipse) und der Steiner-Inellipse.

Trapez

Schwerpunkt eines Trapezes

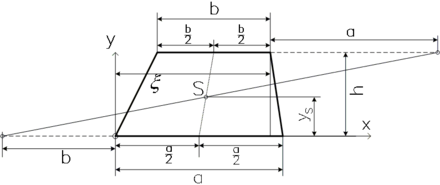
Der Schwerpunkt des Trapezes lässt sich folgendermaßen konstruieren: Eine Schwerelinie halbiert die beiden parallelen Seiten. Eine zweite erhält man, indem man die parallelen Seiten um die Länge der jeweils anderen in entgegengesetzten Richtungen verlängert, und die beiden Endpunkte miteinander verbindet. Die Formel in kartesischen Koordinaten lautet (gemessen vom linken unteren Eckpunkt):

$\begin{align} x_s&=\frac{a^2-b^2+\xi(a+2b)}{3(a+b)}\\ y_s&=\frac{h}{3}\cdot \frac{a+2b}{a+b} \end{align}$

Polygon

Ein Polygon

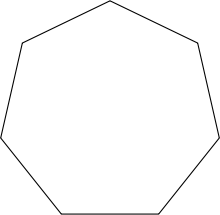
Der Schwerpunkt eines nicht überschlagenen, geschlossenen, auch unregelmäßigen Polygons mit N Eckpunkten kann wie folgt aus den kartesischen Koordinaten (x_i, y_i) der Eckpunkte berechnet werden (der nullte Eckpunkt (x_0, y_0) und der -te Eckpunkt $(x_{N},y_{N})$ sind hierbei identisch). Die Eckpunkte werden fortlaufend gegen den Uhrzeigersinn durchnummeriert. Der Schwerpunkt eines regelmäßigen Polygons entspricht dem Mittelpunkt seines Umkreises.

Der Flächeninhalt des Polygons kann mit der Gaußschen Dreiecksformel

$A = \frac{1}{2}\sum_{i=0}^{N-1} (x_i\ y_{i+1} - x_{i+1}\ y_i)$

bestimmt werden. Der Flächenschwerpunkt des Polygons wird dann mit den Formeln

$\begin{align} x_s &= \frac{1}{6A}\sum_{i=0}^{N-1}(x_i+x_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i)\\ y_s &= \frac{1}{6A}\sum_{i=0}^{N-1}(y_i+y_{i+1})(x_i\ y_{i+1} - x_{i+1}\ y_i) \end{align}$

bestimmt.

Kreisausschnitt

Schwerpunkt eines Kreisteils

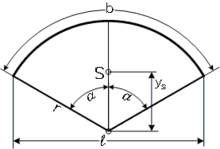
Ist der Ausschnitt des Kreises so gedreht und verschoben, dass die y-Achse des kartesischen Koordinatensystems eine Symmetrieachse des Kreisausschnitts ist und der Mittelpunkt (des Vollkreises) im Ursprung liegt (siehe Bild), dann lässt sich der Schwerpunkt im Bogenmaß durch

$y_s=\frac{2r\sin\alpha}{3\alpha}=\frac{2rl}{3b}$

mit $0 < \alpha \le \pi$ berechnen.

Musste der Kreis anfangs verschoben oder gedreht werden, dann muss zur Vervollständigung der Rechnung der berechnete Schwerpunkt entsprechend wieder zurückverschoben oder gedreht werden.

Kreisabschnitt

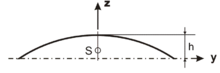
Um den Flächenschwerpunkt eines Kreisabschnitts näherungsweise zu berechnen, muss dieser im kartesischen Koordinatensystem so verschoben werden, dass der Mittelpunkt der Verbindungslinie der beiden Endpunkte im Koordinatenursprung liegt. Dann befindet sich der Schwerpunkt für h<r in guter Näherung etwas oberhalb von

$z_s\approx\frac{2h}5$ .

Bei h=r (Halbkreis) liegt der Schwerpunkt exakt bei $\frac{4r}{3\pi}$ . Die prozentuale Abweichung steigt in etwa proportional mit h und beträgt bei h=r ungefähr 5,8 %. Daraus folgt der Ausdruck $\frac{200h}{500-29h/r}$ , der den Schwerpunkt im Bereich von $(0\leq h\leq r)$ mit einer Genauigkeit von besser als 5 Promille angibt. Die exakte Lage des Flächenschwerpunktes z_s(h) im gesamten Bereich von $(0< h\leq 2r)$ findet man mittels Einsetzen von $\alpha=\arccos(1-h/r)$ in die Formel für den auf den Kreismittelpunkt bezogenen Schwerpunkt $4r \sin(\alpha)^3 /(6\alpha-3\sin(2\alpha))$ :

$z_s=h-r+\frac{2\left(\sqrt{r^2-(h-r)^2}\right)^3}{3\left((h-r)\sqrt{r^2-(h-r)^2}+r^2\arccos (1-h/r)\right)}$ .

War zu Beginn eine Verschiebung oder Drehung notwendig, so muss der Schwerpunkt wieder entsprechend zurückverschoben werden.

Körper

Für dreidimensionale Körper kann man sowohl den Volumenschwerpunkt, also den Schwerpunkt des Vollkörpers, als auch den Flächenschwerpunkt, also den Schwerpunkt der Fläche, die den Körper begrenzt, berechnen.

Pyramide und Kegel

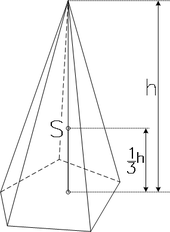
Flächenschwerpunkt einer Pyramide

Um den Volumenschwerpunkt und den Flächenschwerpunkt einer Pyramide oder eines Kegels zu berechnen, verschiebt man sie im schiefwinkligen Koordinatensystem, so dass der Schwerpunkt der Grundfläche im Koordinatenursprung (0,0,0) liegt, und die y-Achse durch die Spitze geht. Dann kann der Volumenschwerpunkt einer Pyramide oder eines Kegels durch

$x_s = 0, \qquad y_s=\frac{h}{4},\qquad z_s = 0$

und der Flächenschwerpunkt der Mantelfläche durch

$x_s = 0, \qquad y_s=\frac{h}{3},\qquad z_s = 0$

berechnet werden.

Rotationsparaboloid

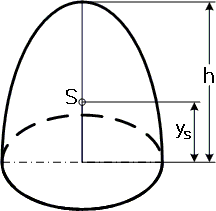
Schwerpunkt eines Rotationsparaboloids

Um den Volumenschwerpunkt und den Flächenschwerpunkt eines Rotationsparaboloids zu berechnen, wird es im kartesischen Koordinatensystem verschoben, so dass der Schwerpunkt der Grundfläche im Koordinatenursprung (0,0,0) liegt. Dann kann man den Volumenschwerpunkt des Rotationsparaboloids durch

$x_s = 0, \qquad y_s=\frac{h}{3},\qquad z_s = 0$

berechnen. Der Flächenschwerpunkt sieht ein wenig komplizierter aus. Für die Komponenten $x_{s}$ und z_s gilt ebenfalls wieder

und die Komponente y_s liegt bei

$y_s=h-\frac{4\pi\sqrt{f}\int_{0}^{h} y \sqrt{f+y}\, \mathrm d y}{4\pi\sqrt{f}\int_{0}^{h} \sqrt{f+y} \, \mathrm d y}=h\left( 1+\frac 25 (f/h)-\frac{3/5}{1-1/(1+h/f)^{3/2}}\right),$

wobei der Ausdruck im Nenner des ersten Bruchs die Mantelfläche der nach rechts geöffneten Parabel $y=2\sqrt{f x}$ mit der Brennweite f darstellt. Ab $(f/h) \gtrsim 3$ strebt y_s gegen $\tfrac 12 h$ , anderenfalls gegen $\tfrac 25 h$ .

Kugelsegment

Schwerpunkt eines Kugelsegments

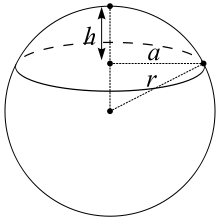
Um den Volumenschwerpunkt und den Flächenschwerpunkt eines Kugelsegments zu berechnen, verschiebt man das Segment im kartesischen Koordinatensystem, so dass der Mittelpunkt der Vollkugel im Koordinatenursprung (0,0,0) liegt. Der Volumenschwerpunkt wird dann durch

$x_s = 0, \quad y_s=\frac{3(2r-h)^2}{4(3r-h)},\quad z_s = 0$

und der Flächenschwerpunkt durch

$x_s = 0, \quad y_s=r-\frac{h}{2},\quad z_s = 0$

berechnet. ( $0\le h \le 2\,r$ )

Zusammenfassen von Schwerpunkten

Es ist möglich, mehrere Schwerpunkte einzelner Figuren zu einem gemeinsamen Schwerpunkt der Gesamtfigur zusammenzufassen, so dass sich der Schwerpunkt einer zusammengesetzten Figur aus den Schwerpunkten einzelner einfacher Elemente ergibt.

eindimensional	zweidimensional	dreidimensional	allgemein
$x_s=\frac{\sum\limits_i (x_{s,i} \cdot l_i)}{\sum\limits_i l_i}$	$x_s=\frac{\sum\limits_i (x_{s,i} \cdot A_i)}{\sum\limits_i A_i}$ $y_s=\frac{\sum\limits_i (y_{s,i} \cdot A_i)}{\sum\limits_i A_i}$	$x_s=\frac{\sum\limits_i (x_{s,i} \cdot V_i)}{\sum\limits_i V_i}$ $y_s=\frac{\sum\limits_i (y_{s,i} \cdot V_i)}{\sum\limits_i V_i}$ $z_s=\frac{\sum\limits_i (z_{s,i} \cdot V_i)}{\sum\limits_i V_i}$	$\vec{r}_s=\frac{\sum\limits_i (\vec{r}_{s,i} \cdot V_i)}{\sum\limits_i V_i}$

Die Koordinaten $x_{s}$ , y_s und z_s sind in einem frei wählbaren, aber einheitlichen kartesischen Koordinatensystem anzugeben. Weist eine Fläche (ein Körper) Aussparungen auf, so können obige Summenformeln ebenfalls angewendet werden unter Berücksichtigung, dass die ausgesparten Flächen (Volumen) mit negativem Vorzeichen in die Berechnung eingehen. Die Komponenten $x_s, \, y_s, \, z_s$ des Schwerpunkts bilden den Vektor ${\vec {r}}_{s}$ .

Definition des Schwerpunkts durch Integrale

Die Formeln zur Berechnung des Schwerpunkts elementargeometrischer Figuren können mit den nachfolgend angegebenen Integralen hergeleitet werden. Bei komplizierteren Figuren lassen sich diese Integrale häufig nur numerisch bestimmen.

Die Definition entspricht mathematisch der Mittelung aller Punkte des geometrischen Objekts (Körpers) im euklidischen Raum $\mathbb {R} ^{3}$ . Bei Linien und Flächen im zweidimensionalen Raum $\mathbb {R} ^{2}$ sind nur die Koordinaten x_S und y_S zu berechnen, die Koordinate entfällt. Der Integrationsbereich ist bei Linien eindimensional, bei Flächen zweidimensional und bei Körpern dreidimensional.

Linien

Für eine Linie der Länge ergibt sich der Schwerpunkt $\vec r_S = (x_S, y_S, z_S)$ durch

$x_S = \frac 1 L \int_K x \,\mathrm dL, \quad y_S = \frac 1 L \int_K y \,\mathrm dL, \quad z_S = \frac 1 L \int_K z \,\mathrm dL$

mit

$\quad L=\int_K \, \mathrm d L.$

Diese Integrale sind Kurvenintegrale erster Art.

Flächen

Für eine Fläche mit Flächeninhalt ist der Schwerpunkt definiert durch

$x_S = \frac 1 A \int_K x\,\mathrm dA, \quad y_S = \frac 1 A \int_K y\, \mathrm dA, \quad z_S = \frac 1 A \int_K z\,\mathrm dA$

mit

$\quad A=\int_K \mathrm dA.$

Diese Integrale sind Oberflächenintegrale mit skalarem Flächenelement.

Körper

Im Fall eines beschränkten Körpers im dreidimensionalen Raum mit Volumen ist der Schwerpunkt definiert durch

$x_S = \frac 1 V \int_K x\,\mathrm dV, \quad y_S = \frac 1 V \int_K y\, \mathrm dV, \quad z_S = \frac 1 V \int_K z\,\mathrm dV$

mit

$\quad V=\int_K \mathrm dV.$

Diese Integrale sind Volumenintegrale.

Allgemein

Sei $K \subset \R^n$ ein Körper mit dem Volumen . Der Schwerpunkt $x_S = (x_{s,1}, \ldots, x_{s,n}) \in \R^n$ von ist definiert durch

$x_{s,i} = \frac{1}{V}\int_K x_i \, \mathrm d V\ \quad\text{mit}\quad V = \int_K \mathrm d V,$

wobei $\mathrm {d} V$ das m-dimensionale Volumenelement und die Dimension von , mit $m\leq n$ ist.

Integration bei symmetrischen Objekten

Bei Objekten die Symmetrieelemente, z.B. eine Symmetrieachse oder eine Symmetrieebene besitzen, vereinfacht sich die Berechnung des Schwerpunkts in vielen Fällen, da der Schwerpunkt immer im Symmetrieelement enthalten ist. Hat das Objekt eine Symmetrieachse, so kann das Volumenelement in Abhängigkeit vom infinitesimalen Achsenelement ausgedrückt werden. Es braucht also nur noch über die Symmetrieachse integriert zu werden.

Beispiele zur Integralrechnung

Linienschwerpunkt eines Kreisbogens

Schwerpunkt eines Kreisbogens

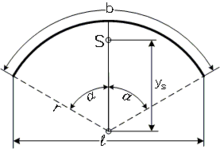
Punkte auf einem ebenen Kreisbogen können am einfachsten in Polarkoordinaten angegeben werden. Wenn die y-Achse auf der Symmetrielinie mit Ursprung im Kreismittelpunkt liegt, lauten die Koordinaten:

$x = r \sin\varphi, \, y = r \cos\varphi.$

Die Länge des Kreisbogens ergibt sich zu:

$b = \int_K \mathrm dL = \int_{-\alpha}^{\alpha} r \mathrm d\varphi = 2 r \alpha,$

wobei das infinitesimale Längenelement $\mathrm dL$ durch $r \mathrm d\varphi$ substituiert werden kann.

Aus Symmetriegründen ist x_S = 0 . Für die y-Koordinate des Linienschwerpunkts ergibt sich aus der Definitionsgleichung:

$y_S = \frac 1 b \int_K y\, \mathrm dL = \frac 1 b \int_{-\alpha}^{\alpha} r^2 \cos\varphi\, \mathrm d\varphi.$

Die Integration in den Grenzen ergibt dann

$y_S = \frac {r^2} b 2 \sin\alpha = r \frac l b.$

Flächenschwerpunkt einer Parabel

Parabel

mit schraffierter Fläche unter der x-Achse; der Schwerpunkt (roter Punkt) liegt bei (0;−1,6).

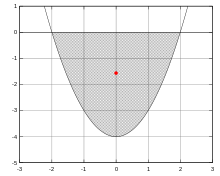
Zur praktischen Bestimmung der x-Koordinate des Schwerpunktes im zweidimensionalen Fall substituiert man $\mathrm {d} A$ mit $y\cdot \mathrm dx$ , was einem infinitesimalen Flächenstreifen entspricht. Ferner entspricht hierbei der die Fläche begrenzenden Funktion y(x) .

Für die praktische Berechnung der y-Koordinate im zweidimensionalen Fall gibt es prinzipiell zwei Vorgehensweisen:

Entweder man bildet Umkehrfunktion und berechnet das Integral $\textstyle \int_A y \mathrm dA = \int_y y\cdot x(y) \ \mathrm dy$ , wobei die „neuen“ Integrationsgrenzen nun auf der y-Achse zu finden sind,
oder man nutzt aus, dass der Schwerpunkt eines jeden zur y-Achse parallelen infinitesimalen Flächenstreifen $\tfrac{y(x)}{2}$ ist. Dann erhält man zur Bestimmung der y-Koordinate eine einfachere Formel, mit deren Hilfe das Bilden der Umkehrfunktion erspart bleibt:

Wir suchen den Flächenschwerpunkt jener Fläche, die durch eine Parabel y = x^2-4 und durch die x-Achse definiert ist (siehe nebenstehende Abbildung).

Zuerst bestimmen wir den Inhalt der Fläche

$A = \left|\int\limits_{-2}^2 (x^2-4)\,\mathrm dx\right| = \frac{32}{3}$

Die Grenzen des Integrals sind bei Begrenzung der Fläche durch die x-Achse die Nullstellen der Funktion.

Die -Koordinate des Schwerpunktes ergibt sich zu

$x_s = \frac{1}{A} \int\limits_{-2}^2 \int\limits_{y(x)}^0 x \, \mathrm dy \,\mathrm dx = -\frac{1}{A} \int\limits_{-2}^2 x\cdot y(x)\,\mathrm dx = -\frac{1}{A} \int\limits_{-2}^2 x\cdot (x^2-4)\,\mathrm dx = 0.$

Die -Koordinate ergibt sich zu

$y_s = \frac{1}{A} \int\limits_{-2}^2 \int\limits_{y(x)}^0 y \, \mathrm dy \,\mathrm dx = -\frac 1{2A}\int\limits_{-2}^2 y(x)^2\,\mathrm dx= -\frac 1{2A}\int\limits_{-2}^2 (x^4-8x^2+16)\,\mathrm dx= -1{,}6.$

Eine andere Möglichkeit die Schwerpunktskoordinaten einer Fläche zu errechnen, ergibt sich durch die Formeln:

$x_s = \frac{\int_{a}^{b}(x(f(x)-g(x)))\, \mathrm d x}{\int_{a}^{b}(f(x)-g(x))\, \mathrm d x}$ , $y_s= \frac{\int_{a}^{b}((f(x))^{2}-(g(x))^{2}) \, \mathrm d x}{\int_{a}^{b} (2(f(x)-g(x) ))\, \mathrm d x},$

wobei die Grenzen und die Schnittpunkte der Funktionen f(x) und g(x) darstellen. Durch diese Formel lässt sich der Schwerpunkt einer beliebigen ebenen Fläche, welche zwischen zwei Funktionen eingeschlossen ist, berechnen. Bedingungen hierfür sind a < x < b , g(x) < y < f(x).

Basierend auf einem Artikel in:

Wikipedia.de