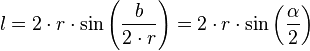Kreisbogen

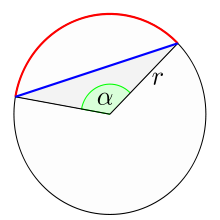
Kreisbogen der Länge b
Kreissehne der Länge l

Legt man auf einem Kreis zwei beliebige Punkte fest und verbindet diese durch Strecken mit dem Mittelpunkt des Kreises, so stellen die beiden Teile der Kreisfläche, die durch diese Strecken voneinander getrennt werden, Kreisausschnitte (auch Kreissektor genannt) dar. Ein Kreisausschnitt wird also gleichsam von zwei Radien aus einem Kreis „herausgeschnitten“. Der zu einem Kreissektor gehörende Teil der Kreislinie wird als Kreisbogen bezeichnet, der Winkel zwischen den beiden Radien als Mittelpunktswinkel.

Berechnung

Die Länge 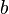eines Kreisbogens mit dem Mittelpunktswinkel α im Gradmaß und dem Radius ist

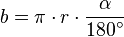$b = \pi \cdot r \cdot \frac{\alpha}{\displaystyle 180^\circ}$ .

Der Flächeninhalt des entsprechenden Kreisausschnittes ist

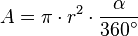$A = \pi \cdot r^2 \cdot \frac{\alpha}{\displaystyle 360^\circ}$ .

Gibt man den Mittelpunktswinkel α im Bogenmaß an, so lauten die Formeln

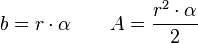$b = r \cdot \alpha \qquad A = \frac{r^2 \cdot \alpha}{2}$ .

Durch Einsetzen des Winkels α = 360° bzw. α = 2π ergeben sich die bekannten Formeln für Umfang und Flächeninhalt des Vollkreises.

Die Kreissehne der Länge 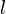bekommt man über folgenden Zusammenhang aus dem Kreisbogen und dem Radius oder direkt aus dem Mittelpunktswinkel:

$l = 2 \cdot r \cdot \sin\left(\frac{b}{2 \cdot r}\right) = 2 \cdot r \cdot \sin\left(\frac{\alpha}{2}\right)$

Siehe auch

Kreissegment ist die Teilfläche eines Kreises, die von einem Kreisbogen und einer Kreissehne begrenzt wird.

Basierend auf einem Artikel in:

Wikipedia.de