Kreissegment
Ein Kreissegment (auch Kreisabschnitt) ist in der Geometrie eine Teilfläche einer Kreisfläche, die von einem Kreisbogen und einer Kreissehne begrenzt wird (im Gegensatz zum von einem Kreisbogen und zwei Kreisradien begrenzten „Kreissektor/Kreisausschnitt“).
Bezeichnungen und Eigenschaften
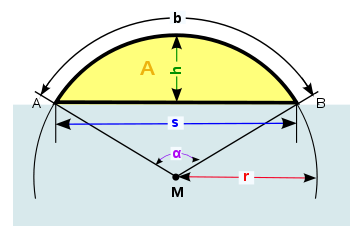
Größen des Kreissegments:
- α = Mittelpunktswinkel
- b = Kreisbogen
- h = Segmenthöhe
- r = Radius
- s = Kreissehne
- A = Segmentfläche
- M = Kreismittelpunkt
Der Flächeninhalt
eines Kreissegments lässt sich aus dem Kreisradius
und dem zugehörigen Mittelpunktswinkel
berechnen. Man ermittelt dazu die Flächeninhalte des entsprechenden
Kreissektors und des in der
Skizze dargestellten gleichschenkligen Dreiecks
AMB. Ist der Mittelpunktswinkel kleiner als 180°, muss man diese Flächeninhalte
subtrahieren (Sektorfläche
minus Dreiecksfläche). Bei einem Mittelpunktswinkel über 180° sind die
Flächeninhalte zu addieren.
Wenn der Mittelpunktswinkel 180° beträgt, ist das Kreissegment eine
Halbkreisfläche und die Fläche des Dreiecks ist 0.
In den Formeln der folgenden Tabelle sind Winkel in Bogenmaß einzusetzen. Die
Umrechnung der Maßzahl
eines Winkels von Grad-
in Bogenmaß erfolgt mit dem Faktor
(s. Radiant).
| Formeln zum
Kreissegment (alle Winkel in Bogenmaß) | |
|---|---|
| Flächeninhalt | |
| Radius | |
| Kreissehne | |
| Segmenthöhe | |
| Bogenlänge | |
| Mittelpunktswinkel | |
| Flächenschwerpunkt | Sonderfall Halbkreis: |
Sagitta
Die Segmenthöhe wird auch Sagitta (lateinisch
für „Pfeil“) genannt, und die dazugehörigen Formeln lassen sich mithilfe des Satzes
von Pythagoras herleiten. Die Strecke der Differenz von Radius und
Segmenthöhe bildet mit der Hälfte der Kreissehne ein rechtwinkliges
Dreieck mit dem Radius als Hypotenuse.
So ergibt sich folgende Gleichung, die sich dann entsprechend umformen lässt:
.
Ähnliche geometrische Objekte
Das dreidimensionale Analogon ist ein Kugelsegment.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.04. 2023