Wirkleistung
Die Wirkleistung ist die elektrische Leistung, die für die Umwandlung in andere Leistungen (z.B. mechanische, thermische oder chemische) verfügbar ist. Sie ist abzugrenzen von der Blindleistung, die für diese Umwandlung nicht verwendbar ist.
Die Wirkleistung
wird in der Einheit Watt
angegeben. Bei gleichbleibender Spannung
und gleichbleibender Stromstärke
ist die Wirkleistung das Produkt von Spannung
und Stromstärke
:
Bei veränderlichen Werten
und
ist die Wirkleistung der Gleichwert
der Augenblicksleistung
:
Für periodische Spannungen und Ströme ist über eine Periode mit der Periodendauer
zu mitteln:
Festlegungen bei sinusförmiger Wechselspannung
Einen wichtigen Anwendungsfall bildet das elektrische Energieversorgungsnetz oder Dreiphasenwechselstromnetz. Nur dieser wird hier behandelt. Die Spannung hat einen sinusförmigen zeitlichen Verlauf; Spannung und Strom sind Wechselgrößen mit derselben Grundfrequenz. Für diesen Fall gibt es Festlegungen in DIN 40108 und DIN 40110, die für diesen Artikel zu beachten sind.
Wirkleistung bei sinusförmigem Strom
Darstellung mit Zeitfunktionen
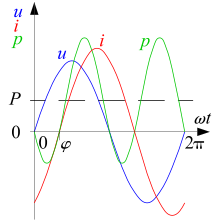
Der sinusförmige Verlauf des Stromes tritt nur dann auf, wenn sich
ausschließlich lineare
Verbraucher im Netz befinden. Bei ohmschen Verbrauchern verlaufen Spannung
und Strom gleichphasig. Beim Auftreten kapazitiver
oder induktiver
Verbraucher tritt zusätzlich eine Verschiebung der Phasenwinkel
zwischen dem Verlauf von Strom und Spannung auf. Mit den Effektivwerten von
Spannung
und Stromstärke
,
den Amplituden
und
,
dem Phasenverschiebungswinkel
>
sowie der Kreisfrequenz
wird
Durch Anwenden der trigonometrischen Beziehung
folgt
und mit der Verwendung der Effektivwerte
Der Ausdruck enthält
- einen zeitunabhängigen Summanden, die Wirkleistung
, und
- einen zeitlich mit doppelter Frequenz und der Amplitude
schwingenden Summanden, dessen Mittelwert gleich null ist. Die Größe
nennt man die Scheinleistung.
Die Komponente
der Stromstärke
,
die für die Wirkleistung maßgeblich ist, wird Wirkstromstärke genannt.
Komplexe Darstellung
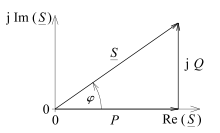
In der Elektrotechnik ist es üblich, die Wechselstromrechnung (also das
Rechnen mit sinusförmigen Wechselgrößen) mit Hilfe von Zeigern in der komplexen
Ebene durchzuführen, da dieses wesentlich einfacher ist als die Rechnung mit
trigonometrischen
Funktionen. Zum Anschluss der Leistungsgrößen an die komplexe
Wechselstromrechnung wird die komplexe Scheinleistung
definiert, die Wirk- und Blindleistung
in einer komplexen Größe zusammenfasst. Sie berechnet sich aus dem Produkt des
komplexen Effektivwertes der Spannung mit dem konjugiert komplexen Effektivwert
der Stromstärke.
Die Scheinleistung ,
also der Betrag der komplexen Scheinleistung
,
ist die pythagoreische
Summe aus Wirk- und Blindleistung. Die Wirkleistung
ist der Realteil,
die Blindleistung
der Imaginärteil
der komplexen Scheinleistung.
Vorzeichenfragen
Die Konventionen über Zählrichtungen der Spannungen und Ströme durch
Erzeuger- und Verbraucher-Bepfeilung bringen es mit sich, dass bei Energiefluss vom Erzeuger
zum Verbraucher die Wirkleistung positiv ist. Das weiter oben gezeigte Bild des
zeitlichen Verlaufs zeigt auch negative Werte von ;
dann wird Energie zurückgespeist. Die Wirkleistung wird dadurch kleiner als die
Scheinleistung; sie bleibt aber positiv.
Bei Netzen mit mehreren Quellen und Lasten kann sich zwischen Netzabschnitten
die Richtung des Energieflusses nicht nur für Bruchteile einer Periodendauer
umkehren. In Blick auf die Leistung beschreibt man dieses durch Vorzeichenumkehr
der Wirkleistung, so dass auch Werte
Sinn haben können.
Wirkleistung bei nichtsinusförmigem Strom
Wenn die Spannung sinusförmig ist, der Strom aber nicht, bleibt die Gleichung
unter der Einschränkung gültig, dass
und
Parameter der Grundschwingung des Stromes sind. Oberschwingungen gehen
in
nicht ein.
Messungen im Energieversorgungsnetz
Messgeräte
Ein Leistungsmesser hat einen Strompfad und einen Spannungspfad. Er multipliziert Augenblickswerte von Spannung und Stromstärke, mittelt über die Augenblickswerte des Produktes und ist somit gemäß der Definition der Wirkleistung ein Wirkleistungsmesser. Das dazu geeignete elektromechanische Messwerk ist durch elektronische Messumformer abgelöst worden.

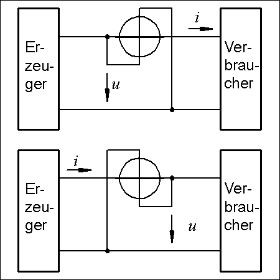
oben: Einphasen-Messgeräte
unten: Dreiphasen-Wirkleistungsmesser
Zu jedem Messgerät gehört ein Messbereich, der nicht überschritten werden darf, weil sonst keine Fehlergrenze garantiert wird. Darüber hinaus gehören zum Leistungsmesser Nennwerte von Spannung und Strom, die nur in geringem Maße gemäß Herstellerangaben überschritten werden dürfen, weil sonst das Gerät beschädigt wird. Diese Art von Überlastung kann durchaus auftreten, ohne den Messbereich zu überschreiten!
Zur vorzeichen-richtigen Messung ist auf korrekten Anschluss zu
achten, der durch korrekte Schaltpläne vorzugeben ist. Für den Regelfall
wird innerhalb dieses Artikels, in Übereinstimmung mit DIN 43807,
konsequent eingehalten:
- Positiver Messwert,
- wenn positiver Energiefluss im Strompfad von links nach rechts
- und positiver Energiefluss im Spannungspfad von unten nach oben.
Falls P negativ ist, aber kein negativer Messwert ausgegeben werden kann, kann man sich durch bewusste Vertauschung der Richtung im Spannungspfad (oder Strompfad) helfen. An Laborgeräten sind die Klemmen eingangsseitig häufig mit einem Stern versehen; Geräte zur dauerhaften Installation tragen eine Klemmen-Nummerierung gemäß DIN 43807; Beispiele siehe Bild.
Jeder Leistungsmesser hat einen Eigenverbrauch
- im Strompfad durch einen Spannungsabfall (wie beim Strommessgerät),
- im Spannungspfad durch eine Stromaufnahme (wie beim Spannungsmessgerät).
Damit ist beim realen Messgerät zwischen Erzeuger- und Verbraucher-Wirkleistung zu unterscheiden.
Einphasennetz
Es gibt zwei Möglichkeiten, den Leistungsmesser anzuschließen, siehe zugehöriges Bild. Keine der Schaltungen erfasst aber die Erzeuger- oder Verbraucher-Wirkleistung, sondern gemessen wird
- in der oberen Schaltung Erzeuger-Spannung mal Verbraucher-Strom,
- in der unteren Schaltung Verbraucher-Spannung mal Erzeuger-Strom.
In der bevorzugt verwendeten oberen Schaltung werden die Kosten des Energie-Verbrauchs des Messgerätes getragen
-
- soweit vom Spannungspfad herrührend durch den Erzeuger,
- soweit vom Strompfad herrührend durch den Verbraucher.

Drehstromnetz
Vierleiter-Stromkreis mit Neutralleiter
Der umfassendste Fall ist der Vierleiter-Stromkreis mit Neutralleiter und
drei Außenleitern, wie er im Niederspannungsnetz mit
= 230 V bzw.
= 400 V verbreitet ist, in Verbindung mit beliebiger Belastung. Beliebig
soll hier heißen: In den drei Außenleitern können Ströme mit unterschiedlichen
Amplituden und unterschiedlichen Phasenverschiebungen zur jeweiligen
Bezugsspannung fließen. Dann ist
Dieses ist messbar mit drei Leistungsmessern bzw. einem Kombinations-Gerät.

Dreileiter-Stromkreis
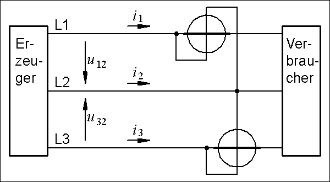
Durch den fehlenden Neutralleiter im Dreileiter-Stromkreis ist
.
Mit
und
wird
wobei der letzte Summand und damit
verschwindet. Im Dreileiter-Stromkreis mit beliebiger Belastung reichen also
zwei Leistungsmesser, wenn man sie in Aronschaltung
gemäß der letzten Gleichung betreibt.
mit
und
,
wobei
= Winkel zwischen
und
und
= Winkel zwischen
und

Hinweise hierzu:
- Formal kann ein Leiter, hier in Übereinstimmung mit DIN 43807 der Leiter L2, als Rückleiter aufgefasst werden.
und
haben keine anschauliche Bedeutung, nicht einmal im Vorzeichen. Z.B. ist bei reiner Blindlast
, aber
.
- Weil
, ist aufzupassen, ob der Leistungsmesser, der auf die Spannung
ausgelegt ist, auch die höhere Spannung
verträgt. Wenn durch einen Vorwiderstand oder einen Spannungswandler die Spannung um den Faktor
vermindert wird, ist diese Überlastungsgefahr behoben. Wegen der so verkleinerten Spannung muss allerdings der Messwert um den Faktor
rechnerisch vergrößert werden.

Symmetrische Belastung
Bei symmetrischer Belastung reicht die Verwendung nur eines Leistungsmessers für den Leistungs-Bezug durch einen der Außenleiter. Die gesamte Leistung ist davon das Dreifache.
.
Im Dreileiter-Stromkreis ist dazu das Neutralleiter-Potential durch einen Sternpunkt gemäß Bild künstlich zu schaffen mit zwei Widerständen, die genauso groß sind wie der Widerstand des Spannungspfades im Leistungsmesser.
Weitere Benennungen
| Benennung | Größe | Anwendung |
|---|---|---|
| Leistungsfaktor | allgemein | |
| Verschiebungsfaktor | bei Sinusgrößen | |
| Wirkfaktor | bei Sinusgrößen | |
| Blindfaktor | bei Sinusgrößen | |
| Verlustfaktor | bei Sinusgrößen bei Kondensatoren und Spulen |
Alle Angaben stimmen mit DIN 40110-1:1994 überein.
Siehe auch
- Impedanz (Wechselstromwiderstand)
- Blindwiderstand


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.05. 2024