Blindstrom

Die Begriffe Blindstrom und Wirkstrom finden Verwendung in der Elektrotechnik, insbesondere im Zusammenhang mit der Übertragung von elektrischer Energie. Häufig ist der Augenblickswert der Stromstärke nicht proportional zum Augenblickswert der elektrischen Spannung. Während die elektrische Wechselspannung als eingeprägte Spannung fast immer nahezu sinusförmig verläuft, kann die Wechselstromstärke zeitlich verschoben oder in der Form verändert (verzerrt) sein.

Ein Beschreibungsmodell ist die Aufspaltung in zwei Komponenten, von denen die eine proportional zur Spannung ist und als Wirkstromstärke i_p bezeichnet wird. Die dazu orthogonale andere Komponente ist die Blindstromstärke i_q (zur Orthogonalität siehe Anmerkung).

Die Stromstärke

lässt sich zusammengesetzt denken aus einer Wirkstromstärke (Kurve 1) und einer Blindstromstärke (Kurve 2)

Während der Wirkstrom für die elektrische Arbeit oder den Transport von elektrischer Energie steht, die beim Verbraucher in mechanische, thermische oder chemische Energie umgewandelt wird, ist der zusätzlich fließende Blindstrom daran unbeteiligt.

$u\,\sim i_p$

bzw. für den Effektivwert $I_q =\sqrt {I^2- I_p^2}$

Auslöser von Blindstrom sind

nichtlineare Bauelemente, die eine Verzerrung hervorrufen (Verzerrungsblindstrom), sowie
kapazitive oder induktive Bauelemente, die eine Phasenverschiebung zwischen Spannung und Strom hervorrufen (Verschiebungsblindstrom).

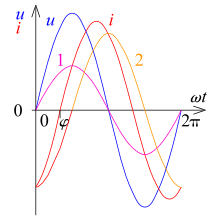
Sinusförmiger Strom- und Spannungsverlauf

Bei sinusförmiger Spannung mit dazu nicht proportionaler sinusförmiger Stromstärke

gibt es Zeiten, in denen Energie zurückgespeist wird (wenn die Leistung negativ ist)

Wenn bei einem linearen Verbraucher die Augenblickswerte von und nicht zueinander proportional sind, so ist die eine Größe gegenüber der anderen in ihrem Phasenwinkel verschoben. Der Wirkstrom ist derjenige Stromanteil, welcher mit der Spannung im Phasenwinkel übereinstimmt. Der Blindstrom ist derjenige Stromanteil, welcher zur sinusförmigen Spannung um 90° verschoben ist. Man unterscheidet zwischen kapazitivem Blindstrom, welcher der Spannung um 90° voreilt, und induktivem Blindstrom, welcher der Spannung um 90° nacheilt, je nachdem, ob der Blindstrom durch Kapazitäten (Kondensatoren oder Leitungskapazität) oder Induktivitäten (induktive Verbraucher oder Leitungsinduktivität) entsteht.

Bei einem Phasenverschiebungswinkel $\varphi$ kann der Effektivwert der Stromstärke aufgespalten werden in eine Wirkstromstärke

$I_p = I \cdot |\cos \varphi|$

und eine Blindstromstärke

$I_q = I \cdot |\sin \varphi|\ .$

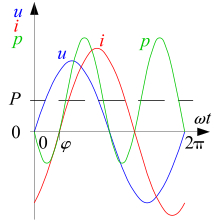
Damit verbunden sind die Begriffe Wirkleistung

$P=U\,I\cdot \cos \varphi \ ,$

Verschiebungsblindleistung (wenn keine Verwechselung möglich ist, einfach Blindleistung)

$Q=U\,I\cdot \sin \varphi$

und Gesamtblindleistung

$Q_\text{tot} = U\,I_q =\sqrt {S^2-P^2} =|Q|\ .$

Dabei steht für die Scheinleistung.

Wirkstrom ohne begleitenden Blindanteil entsteht durch ohmsche Verbraucher, z.B. konventionelle Heizgeräte. Generell entsteht Wirkstrom bei allen Verbrauchern, die in ihrem elektrischen Widerstand einen ohmschen Anteil aufweisen. Im Niederspannungsnetz kann aufgrund der Leitungsinduktivität und vieler induktiver Verbraucher (z.B. Motoren, Transformatoren, Vorschaltgeräte, Induktionsöfen usw., also Spulen jeglicher Art) ein erheblicher induktiver Blindstrom auftreten, der zur Erzeugung von Magnetfeldern benötigt wird, die im Rhythmus der Wechselspannung auf- und abgebaut werden; der Blindstrom steht somit für den Transport von Energie, die zwischen Erzeuger und Verbraucher pendelt. Diesen Strom möchte man auf den Leitungen reduzieren oder vermeiden, da er an deren ohmschen Widerständen eine Verlustleistung bewirkt.

Bei Antrieben mit Asynchronmaschinen ist der Blindstrombedarf durch den Motor definiert und weitgehend unabhängig von der mechanischen Antriebsleistung. Da der Blindstrom den Strom im Stromnetz unnötig erhöht, stellen die Energieversorgungsunternehmen Großabnehmern die vom Blindstrom verursachte Blindarbeit („Blindleistungsverbrauch“) in Rechnung. Daher betreiben die Großabnehmer Einrichtungen zur Blindstromkompensation. Diese sind in erster Linie Kondensatoren, die einen kapazitiven Blindstrom aufnehmen, der dem üblicherweise induktiven Blindstrom der Verbraucher entgegengesetzt gerichtet ist und ihn näherungsweise aufhebt.

Im Hochspannungsnetz entsteht durch den Kapazitätsbelag der Leitungen kapazitiver Blindstrom, der jedoch weitgehend im Niederspannungsnetz kompensiert wird. In Erdkabeln wirkt der Blindstromanteil allerdings begrenzend auf die realisierbare Kabellänge.

Nicht sinusförmiger Stromverlauf

Bei nicht sinusförmigem oder „verzerrtem“ Wechselstrom, der bei nicht linearen Verbrauchern wie beispielsweise Stromrichtern trotz sinusförmiger Spannung auftritt, muss das Beschreibungsmodell auf die sinusförmige Grundschwingung und deren Oberschwingungen mit ganzzahligen Vielfachen der Netzfrequenz erweitert werden. Die Stromanteile mit Oberschwingungen werden zusammenfassend als Oberschwingungsstrom oder Verzerrungsstrom i_d bezeichnet. Sie bewirken bei sinusförmiger Netzspannung im zeitlichen Mittel ebenfalls keine Energieübertragung, sondern nur eine sogenannte Verzerrungsblindleistung.

Bezeichnet man die Stromkomponente mit der gegenüber der Grundfrequenz -fach höheren Frequenz mit i_n , so ergibt sich

(nur Grundschwingung vorhanden)

bzw. für den Effektivwert $I_d =\sqrt {I^2- I_1^2}= \sqrt{ I_2^2 + I_3^2 + \cdots}\ .$

Der Effektivwert der gesamten Wechselstromstärke ergibt sich als pythagoräische Summe der Grundschwingungsstromstärke und Oberschwingungsstromstärken zu

$I = \sqrt{I_1^2 + I_2^2 + I_3^2 + \cdots} = \sqrt{\sum_{n=1}^\infty I_n^2}\ .$

Von der gesamten Stromstärke geht einzig der Wirkanteil des Grundschwingungsstromes

$i_{p1}=i-i_{q1}-i_d$

in die Wirkleistung ein,

$P=P_1 = U\,I_1 \cdot \cos \varphi_1\ .$

Zusätzlich zur Verschiebungsblindleistung der Grundschwingung

$Q_1 = U\,I_1 \cdot \sin \varphi_1$

verursacht der Verzerrungsstrom die Verzerrungsblindleistung

$Q_d = U\,I_d$

und zusammen die Gesamtblindleistung

$Q_\text{tot} = \sqrt {Q_1^2+Q_d^2} =\sqrt {S^2-P^2}\ .$

Nicht sinusförmiger Spannungsverlauf

In diesem bei der elektrischen Energieübertragung weniger wichtigen, aber bei Schaltnetzteilen bedeutsamen Fall gilt für den gesamten Wirkstrom

$I_p = \sqrt {\sum_{n=1}^\infty I_{pn}^2}$

und den gesamten Blindstrom

$I_q = \sqrt {\sum_{n=1}^\infty I_{qn}^2} = \sqrt{I^2-I_p^2}$

Messung von Wirk- und Blindstrom

Bei sinusförmigem Strom eignet sich zur Messung von Wirkstrom (im üblichen Bereich $-\pi /2<\varphi <\pi /2$ ) der gesteuerte Gleichrichter, dessen arithmetisch gemittelte Ausgangsspannung proportional zu

$I\cdot \cos \varphi$

ist. Dem Messgerät muss zusätzlich zum Strom auch die Bezugsspannung zugeführt werden. Bei verzerrtem Strom wird das Ergebnis durch ungeradzahlige Oberschwingungen beeinflusst.

Mit einer zur Bezugsspannung um +90° oder –90° verschobenen Spannung (so gewählt, dass die gemittelte Ausgangsspannung positiv wird) wird entsprechend

$I \cdot |\sin \varphi|$

messbar.

Anmerkung

Als orthogonal zur Spannung werden alle Anteile i_k an der Stromstärke bezeichnet, bei denen die Bedingung $\int\limits_0^T u\cdot i_k \,\mathrm dt =0$ erfüllt ist.

Beispiel 1: Zu $u=\hat u_1 \sin \omega t$ orthogonal ist ein Stromanteil $i_1=\hat\imath_1 \cos \omega t$ .

Die beiden Größen sind sinusförmig und von gleicher Frequenz, unterscheiden sich aber im Phasenwinkel um 90°.

Beispiel 2: Zu $u=\hat u_m \sin m\omega t$ orthogonal sind die Stromanteile $i_n=\hat\imath_n \sin (n\omega t+\varphi_n)$ , wenn $m \ne n$ .

Die beiden Größen sind sinusförmig, unterscheiden sich aber in der Frequenz um einen rationalen Faktor ≠ 1.

Basierend auf einem Artikel in:

Wikipedia.de