
Blindleistung
Blindleistung ist ein Begriff der Elektrotechnik. Sie tritt auf, wenn elektrische Energie über Wechselstrom transportiert wird, wie üblicherweise im Stromnetz zwischen Kraftwerk und Verbraucher. Anstatt die elektrische Energie beispielsweise als Wärme oder Bewegungsenergie abzugeben, wird von manchen Elektrogeräten kurzzeitig Energie gespeichert und wieder ins Netz zurückgespeist. So „pendelt“ im Netz elektrische Energie zwischen Erzeuger und Verbraucher. Diese bedingt einen zusätzlichen Blindstrom; die damit verbundene Leistung heißt Blindleistung. Sie ist weitgehend unerwünscht.
Die Hauptverursacher der Blindleistung im Wechselstromnetz sind in Verbrauchern enthaltene Spulen und Kondensatoren. Diese bauen in jeder Netz-Halbschwingung ein magnetisches oder elektrisches Feld auf und wieder ab. Dabei wird im magnetischen Feld gespeicherte elektrische Energie nach der Vorzeichenumkehr der Spannung ins Netz zurückgespeist; entsprechendes gilt beim elektrischen Feld nach der Vorzeichenumkehr der Stromstärke. Diese Art von Blindleistung ist mit einer Phasenverschiebung zwischen Spannung und Stromstärke verbunden. Sie kann durch besondere Betriebsmittel reduziert (kompensiert) werden.
Neben dieser Verschiebungsblindleistung gibt es Verzerrungsblindleistung, wenn die Stromstärke nicht sinusförmig ist.
Die beim Verbraucher „tatsächlich etwas bewirkende“ elektrische Leistung heißt Wirkleistung.
Elektrizitätsversorger berechnen Privathaushalten nur die Wirkenergie, die Blindenergie nicht.
Festlegungen
Der Artikel verwendet für die Richtungsfestlegung das in der Elektrotechnik weitgehend übliche Verbraucherzählpfeilsystem.
Bei Gleichgrößen
wird die elektrische
Leistung
aus Spannung
und Stromstärke
definiert.
Bei Wechselgrößen
wird entsprechend der Augenblickswert
der Leistung
aus den Augenblickswerten der Spannung
und der Stromstärke
definiert. Anstelle der Augenblickswerte werden möglichst durch Mittelwertbildung
(Integration) gewonnene, in stationären
Vorgängen konstante Größen verwendet:
- die Effektivwerte
der Spannung
und der Stromstärke
- drei Leistungsangaben
- die Wirkleistung
- die Scheinleistung
- die Gesamtblindleistung
- die Wirkleistung
Diese Definitionen gelten gemäß Normung allgemein.
Die Einheit der Leistung ist das Watt
(Einheitenzeichen
W). In der elektrischen Energietechnik werden gemäß derselben Normen – auch in
DIN 1301-2 („Einheiten“) – vorwiegend für die Scheinleistung das Voltampere (Einheitenzeichen
VA) und für die Blindleistung das Var
(Einheitenzeichen var) benutzt; dabei gilt .
Für das Versorgungsnetz sind weitere Festlegungen in DIN 40108 und DIN 40110-2 zu beachten.
Sinusförmige Spannungen und Ströme
Verschiebungsblindleistung
Für die Anwendung im Energieversorgungsnetz sind
und
Wechselgrößen mit derselben Grundfrequenz.
Wenn sie außerdem beide sinusförmig sind mit
und
,
dabei möglicherweise um den Phasenverschiebungswinkel
verschoben, sowie mit den Amplituden
und
,
gilt gemäß der Herleitung
der Wirkleistung
.
Durch die Phasenverschiebung entsteht eine Verschiebungsblindleistung.
Zur ihrer Herleitung
wird die Stromstärke
mit einem Additionstheorem
zerlegt in
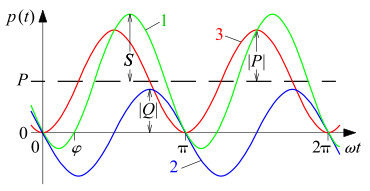
Die vom Verbraucher aufgenommene Leistung (Kurve 1) setzt sich zusammen aus einem zur Wirkleistung beitragenden Anteil (Kurve 3) und einem Rest, der zur Blindleistung beiträgt (Kurve 2)
.
Das stellt eine im Phasenwinkel
mit der Spannung
übereinstimmende Wirkstromstärke
dar und eine dagegen um 90° versetzte Blindstromstärke. Damit ist der
Augenblickswert der Leistung
und mit den Doppelwinkelfunktionen
.
Diese Gleichung wird in nebenstehendem Diagramm aufgeschlüsselt. Kurve 2
zeigt den zweiten Summanden als eine Schwingung um die Höhe null, die damit im
zeitlichen Mittel nichts zum Energiefluss
beiträgt. Der Faktor
in diesem Summanden dient in Analogie zur Definition der Wirkleistung zur
Definition der Verschiebungsblindleistung
.
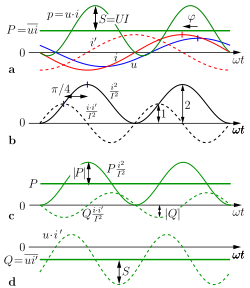
Mittelwertdefinition Die gleichwertige Definition
,
aus welcher die zuerst angegebene folgt, bestimmt die
Verschiebungsblindleistung als arithmetischen Mittelwert aus Momentanwerten des
Sinusvorgangs. Darin steht
(Grafik a) für die um
vorlaufend verschobene Stromstärke. Für jeden Sinusvorgang mit
,
und der Periode
folgt aus dem Mittelwert
die oben angegebene Formel .
Herleitung
Die Augenblicksleistung eines einzelnen Widerstands lässt sich durch
ausdrücken, die einer idealen Spule und die eines idealen Kondensators durch
bzw.
.
Beim Widerstand gibt das Produkt
seine Wirkleistung
an, bei der Spule und dem Kondensator bezeichnen
bzw.
deren Blindleistung
.
Diese für die drei elementaren Schaltelemente gültige Vorüberlegung
motiviert dazu, für die Augenblicksleistung
eines linearen passiven oder aktiven Zweipols den Zerlegungsansatz
zu erproben. Der orthogonale[2]
Zerlegungsansatz separiert die Augenblicksleistung eines Zweipols wie eine aus
Widerstand und Induktivität gebildete Reihenersatzschaltung, daran erkennbar,
dass die Stromstärke
dem ohmschen (linken) und induktivem (rechten) Summanden gemeinsam ist.
Die Mittelung beider Seiten der Ansatzgleichung liefert die Wirkleistung des
Zweipols ,
wobei benutzt wird, dass die Mittelwerte der bei
und
stehenden Zeitfunktionen eins bzw. null betragen (Grafik b).
Ebenso ist die Blindleistung zu bestimmen. Dazu wird die Zerlegungsgleichung
auf beiden Seiten mit
multipliziert, um die Zeitfunktion bei
quadratisch in
zu formulieren. Aus
folgt durch Mittelung
,
da jetzt die Zeitfunktion zu
den Mittelwert null und die zu
den Mittelwert eins hat. Die Definition gilt in allen vier Quadranten der
-
-Ebene
im Verbraucher- und Erzeugerzählpfeilsystem in gleicher Gestalt.
Die Gesamtblindleistung bei Sinusverläufen ergibt sich gemäß der Festlegung oben zu
.
Wenn keine Verwechselung möglich ist, heißt die Verschiebungsblindleistung
allein Blindleistung mit .
Die beiden möglichen Vorzeichen von
kennzeichnen zwei Arten von phasenverschiebenden passiven Zweipolen (Verbrauchern):
| Induktiver Verbraucher:
Die Stromstärke eilt der Spannung nach |
| |
| Kapazitiver Verbraucher:
Die Stromstärke eilt der Spannung voraus |
|
Bei der Zusammenschaltung zweier aktiver Zweipole kann sich der
Phasenverschiebungswinkel auch im Bereich von −180° bis +180° bewegen.
Beispielsweise arbeitet die Synchronmaschine
eines Pumpspeicherkraftwerks
im Turbinenbetrieb als Generator
oder im Pumpbetrieb als Motor
.
In beiden Fällen kann die Maschine nach Bedarf kapazitiv
oder induktiv
wirkend eingesetzt werden (Vierquadrantenbetrieb). Am Verknüpfungspunkt mit dem
Netz ist der vollständige Bereich des Phasenverschiebungswinkels zu messen.
In der Elektrotechnik ist es üblich, die Wechselstromrechnung (also das Rechnen mit sinusförmigen Wechselgrößen) mit Hilfe von Zeigern in der komplexen Ebene durchzuführen, da dieses wesentlich einfacher ist als die Rechnung mit trigonometrischen Funktionen. Dann ist in der komplexen Wechselstromrechnung die Blindleistung der Imaginäranteil der komplexen elektrischen Leistung.
Ursache
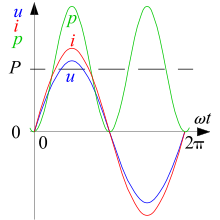
Bei ohmscher
Belastung haben Spannung und Strom einen phasengleichen Verlauf, der
Phasenverschiebungswinkel ist .
Die gesamte vom Erzeuger gelieferte Energie wird beim Verbraucher umgesetzt
(z.B. als thermische oder chemische Energie).
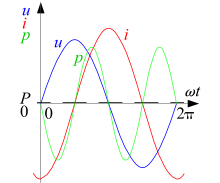
Bei einem induktiven
Verbraucher (z.B. Drosselspule,
Transformator, Asynchronmotor) wird vom
Erzeuger gelieferte Energie verwendet, um das magnetische Feld
aufzubauen. Die Energie wird zunächst im Magnetfeld gespeichert, jedoch mit dem
periodischen
Wechsel im Vorzeichen der Spannung wird das Feld wieder abgebaut und die Energie
ins Netz zurückgespeist. Bei rein induktiver Belastung läuft der Strom der
Spannung um eine Viertelperiode nach, der Phasenverschiebungswinkel beträgt 90°.
Das Produkt aus
und
befindet sich abwechselnd im positiven und negativen Bereich, wobei die Frequenz
der Leistung die doppelte der Grundfrequenz ist. Wenn sich die Leistung
im negativen Bereich befindet, bedeutet das, dass Energie in das Netz
zurückgeliefert wird. Die Leistung schwankt um ihre mittlere Höhe null, was
zeigt, dass Energie im Netz nur hin- und herpendelt. Sie erzeugt aber „blinden“ Stromfluss. Für
diesen Fall ergibt sich
Entsprechendes gilt auch für kapazitive Verbraucher (z.B. Kondensatormotoren, Erdkabel), die jedoch statt des magnetischen ein elektrisches Feld erzeugen, das eine Phasenverschiebung zwar in der anderen Richtung einstellt, aber sonst dasselbe liefert: Die zum Auf- und Abbau des Feldes pro Periode transportierte Energie stellt Blindleistung dar.
Zur Klarstellung: Wirkleistung steht für Energieverbrauch, bei dem elektrische Energie bezogen und meistens irreversibel in eine andere Energieform umgesetzt wird. Verschiebungsblindleistung steht dagegen für Energiebedarf, bei dem elektrische Energie bezogen, für einen Bruchteil einer Netzperiode gespeichert und dann wieder reversibel in das Netz eingespeist wird.
Die Blindleistung tritt in der Regel bei allen am Netz angekoppelten Komponenten und auch beim Leitungsnetz selbst auf. Da in einem Stromkreis im Prinzip immer die drei passiven linearen Eigenschaften Kapazität, Induktivität und ohmscher Widerstand entweder in diskreten Bauelementen oder als „Leitungsbelag“ vorhanden sind, liegt in einem Wechselstrom-Versorgungsnetz praktisch immer eine Blindleistungsbelastung vor.
Belastung durch Blindleistung
Übersicht zum Auftreten von Blindleistung
Blindleistung tritt in den folgenden Bereichen auf:
- unvermeidlich durch an das Stromnetz angeschlossene induktive bzw. kapazitive Verbraucher und das Netz selbst (siehe Abschnitt oberhalb)
- gezielt durch Einstellung des Erregerstroms in Synchronmaschinen in Kraftwerken zur zentralen Blindleistungs-Kompensation, Einstellung der Netzspannung und Lastfluss-Steuerung
- durch gezielten dezentralen Blindleistungs-Bedarf, um
- dezentral erforderliche Blindleistung zu kompensieren oder
- die Spannung am Netzverknüpfungspunkt zu beeinflussen
Beispiel zum letzten Punkt: Photovoltaik-Wechselrichter ab 13,8 kVA
Scheinleistung verhalten sich gemäß VDE AR-N-4105 in der Standardeinstellung bei
Volllast mit induktivem Blindleistungs-Bedarf mit ,
weil dadurch die Spannung am Einspeisepunkt gesenkt wird. Dies soll der Erhöhung
der Netzspannung am Einspeisepunkt durch den ohmschen Widerstand entgegenwirken,
und so die Einspeisung einer höheren Leistung ermöglichen, bevor der
Wechselrichter bei einer Netzspannung von 253 V vom Netz gehen müsste.
Folgen
Die Leistung
wird über das Versorgungsnetz bezogen, wenn Spannung und Strom dasselbe
Vorzeichen haben. Wenn die Vorzeichen gegensätzlich sind, wird die Leistung
wieder zurückgespeist. Die Rückspeisung bewirkt eine Blindleistung und einen Blindstrom, der bei
steigendem Blindleistungsbedarf der Verbraucher ansteigt. Um der Erwärmung der
Leitung entgegenzuwirken, werden größere Leiterquerschnitte in den
Versorgungsleitungen sowie größere Generatoren und
Transformatoren nötig. Elektrische Großverbraucher in der Industrie müssen neben
der bezogenen Wirkenergie auch für ihren Blindenergiebezug bezahlen. Privat- und
Kleinverbraucher, die im Gegensatz zur Industrie überwiegend Strom für die
Wärmeerzeugung beziehen, verursachen geringe Blindleistungsbelastung und werden
deswegen und wegen des hohen Aufwandes für deren Erfassung von den Kosten
freigestellt, oder die Kosten finden sich im Preis der Wirkarbeit (angegeben in
kWh) wieder. – Außerdem bewirken Blindlaständerungen wesentlich größere
Spannungsänderungen im Netz, da der Innenwiderstand von Generatoren und
Transformatoren überwiegend induktiv ist.
- Beispiel einer Blindleistung
Erdkabel stellen aufgrund des geringen Abstandes der Adern zueinander bei gegebener Länge eine große kapazitive Last dar. Die rund 11,5 km lange 380-kV-Transversale Berlin hat eine Kapazität von 2,2 μF. Um diese mit 50 Hz umzuladen, muss Blindstrom von 160 A aufgebracht werden, das entspricht einer Blindleistung von 110 Mvar. Deshalb ist die sinnvolle maximale Kabellänge auf etwa 70 km begrenzt.
Gegenmaßnahmen
Durch geeignete Maßnahmen versuchen die großen Energieverbraucher, den Blindleistungsbedarf möglichst gering zu halten. Der induktive Blindleistungsbedarf einer Asynchronmaschine kann durch eine Kondensatorbatterie, Synchronmaschine oder einen speziellen Stromrichter (Leistungsfaktorkorrektur) kompensiert werden, das wird als Blindleistungskompensation bezeichnet. Die für die Erzeugung des magnetischen Feldes erforderliche Energie pendelt dann nicht mehr in das versorgende Netz bis zum Generator, sondern nur zwischen Asynchronmaschine und Kondensatorbatterie oder Synchronmaschine. Damit sinkt der resultierende Strom, den der Antrieb aus dem Netz entnimmt. Das oberste Bild verdeutlicht das in den drei gezeigten Kurven:
- Kurve 1: Von Maschine aufgenommene Leistung; sie schwingt mit der
Amplitude
.
- Kurve 2: Von Kondensator zu liefernde Leistung; sie schwingt mit der
Amplitude
.
- Kurve 3: Dann noch vom Netz bezogene Leistung; sie schwingt mit der
Amplitude
.
Bei Antrieben mit Asynchronmaschinen ist der Blindleistungsbedarf durch den Motor definiert und weitgehend unabhängig von der mechanischen Antriebsleistung. Die Kompensation mit Hilfe einer Kondensatorbatterie, Synchronmaschine oder einem speziellen Stromrichter (Leistungsfaktorkorrektur) ist möglich. Bei Systemen mit veränderlichem Blindleistungsbedarf ist es erforderlich, dass anstelle einer Kompensationseinrichtung mit konstanter Blindleistung (Kondensator) ein geregelter Kompensator eingesetzt wird.
Die Blindleistungen innerhalb eines regionalen Stromnetzes können durch Phasenschiebertransformatoren oder rotierende Phasenschieber kompensiert werden.
Die Parallelschaltung von Kapazität und Induktivität zu diesem Zweck kann auch als Schwingkreis angesehen werden, der bei passender Auslegung bei 50 Hz seine Resonanzfrequenz hat und Blindstrom sperrt. Ein Beispiel wird unter Blindleistungskompensation dargestellt.
Nichtsinusförmige Ströme
Bei sinusförmiger Spannung können auch nichtsinusförmige Ströme auftreten. Das ist bei allen nichtlinearen Verbrauchern, wie Umrichtern in der Leistungselektronik oder bei Induktivitäten, die magnetisch sättigen, der Fall. Nichtsinusförmige Ströme können auch bei Netzteilen ohne Leistungsfaktorkorrektur auftreten. Siehe hierzu auch Stromflusswinkel.
Bei einem solchen Strom handelt es sich um eine Summe von sinusförmigen
Anteilen unterschiedlicher Frequenz; er beinhaltet neben dem Grundschwingungsanteil
auch noch Oberschwingungsanteile.
Wird mit
der Effektivwert der Grundschwingung bezeichnet, mit
,
… die Effektivwerte der Oberschwingungen, so gilt für die Wirkleistung
nur die Parameter der Grundschwingung des Stromes sind von Bedeutung;
Oberschwingungen haben auf
keinen Einfluss. Dagegen gehen bei der Schein- und Blindleistung alle
Oberschwingungen mit in das Ergebnis ein.
Mit der Gesamtblindleistung
einer Verschiebungsblindleistung in der Grundschwingung
und einer Verzerrungsblindleistung in den Oberschwingungen
ergibt sich
Blindleistungsmesser, soweit sie wie nachfolgend beschrieben wie
Wirkleistungsmesser arbeiten, erfassen (bei sinusförmiger Spannung) nur .
Elektronische Geräte mit genügend schneller digitaler Abtastung und Berechnung
lassen auch die Messung von
zu.
Mehrphasensystem
Im Abschnitt Ursache im ersten Bild ist ersichtlich, dass bei sinusförmiger Spannung und ohmscher Last die Augenblicksleistung zwar keine negativen Augenblickswerte hat, aber schwankt. Es tritt also ein Mittelwert auf (die Wirkleistung) und eine Leistungsschwankung, die jedoch in diesem Fall keine Blindleistung ist.
Beim Übergang zum symmetrischen Dreiphasensystem verdreifacht sich die Wirkleistung. Wegen des Wegfalls der Rückleiter (es sind statt 6 Leitern nur 3 erforderlich) steigen die Zuleitungsverluste nur um den Faktor 1,5. Diese Einsparung der Zuleitungsverluste lässt sich damit erklären, dass im symmetrisch belasteten Dreiphasennetz die Summenleistung zeitlich konstant ist, also keine Leistungspendelung auftritt.
Bei unsymmetrischer Last treten im Neutralleiter zusätzliche Verluste auf, sie sind dem zeitlichen Verlauf der Summenleistung als Pendelungen überlagert. Dieser Effekt wird mit Unsymmetrie-Blindleistung beschrieben.
Messungen im Energieversorgungsnetz
Dieser Abschnitt beschränkt sich auf den Fall, dass Spannung und Strom sinusförmig sind, aber mit einer Phasenverschiebung.
Messgeräte
Ein Leistungsmesser hat einen Strompfad und einen Spannungspfad. Er multipliziert Augenblickswerte von Spannung und Stromstärke, mittelt über die Augenblickswerte des Produktes und ist somit gemäß der Definition der Wirkleistung ein Wirkleistungsmesser. Alternativ ist das Gerät zur Messung der Blindleistung geeignet, wenn die Spannung am Spannungspfad um 90° nacheilt gegenüber der Spannung am Verbraucher. Bei Messgeräten, die nur positive Werte ausgeben können, muss die Spannung bei kapazitiver Blindlast zur Vermeidung negativer Messwerte umgepolt worden.
Wenn die Spannungen am Verbraucher
und am Spannungspfad
denselben Effektivwert haben, wird gemessen
Im Einphasennetz ist zur Phasenverschiebung eine Kunstschaltung erforderlich, z.B. die Hummelschaltung, die mit zwei verlustbehafteten Spulen und einem ohmschen Widerstand bei einer festgelegten Frequenz eine Verschiebung um 90° erzeugt.
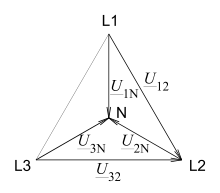
Um 90° verschobene Spannungen – in der Zeigerdarstellung in der komplexen
Ebene um 90° gedrehte Spannungen – sind im unverzerrten Dreiphasennetz
mit Neutralleiter direkt verfügbar. Beispielsweise zu
um 90° nacheilend ist
.
Allerdings unterscheiden sich die Spannungen im Betrag:
.
Durch einen Vorwiderstand
oder einen Spannungswandler
lässt sich die Spannung aber um den Faktor
vermindern; je nach Umständen kann das Ergebnis auch rechnerisch korrigiert
werden.
Zur vorzeichen-richtigen Messung ist auf korrekte Anschlüsse der Pfade
zu achten, die durch korrekte Schaltpläne vorzugeben sind. Die vorhandene
Normung für den Regelfall
wird innerhalb dieses Artikels in den Schaltplänen konsequent angewendet. Wie
die Einfügung eines Messgerätes in die Schaltung anhand des Schaltplans
dargestellt wird, wie die Darstellung anhand der Kennzeichnung der Pfadklemmen
in die Schaltung übernommen wird, was beim Messgerät noch zu beachten ist, wird
unter dem Stichwort Wirkleistungsmessung
erläutert.
Einphasennetz
Die übliche Schaltung entspricht der Schaltung zur Wirkleistungsmessung, nur dass der Strom durch den Spannungspfad gegenüber der Spannung um 90° verschoben werden muss,– in der Regel wie oben angegeben: Spannung am Spannungspfad um 90° nacheilend gegenüber der Spannung am Verbraucher.
Dreiphasennetz
Vierleiter-Stromkreis mit Neutralleiter

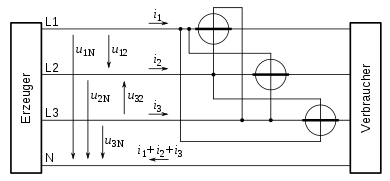
Der umfassendste Fall ist der Vierleiter-Stromkreis mit Neutralleiter und
drei Außenleitern, wie er im Niederspannungsnetz mit
= 230 V oder
= 400 V verbreitet ist, in Verbindung mit beliebiger Belastung. Beliebig
soll hier heißen: In den drei Außenleitern können Ströme mit unterschiedlichen
Amplituden und
unterschiedlichen Phasenverschiebungswinkeln zur jeweiligen Bezugsspannung
fließen. Damit ist die Blindleistung messbar mit drei Leistungsmessern oder
einem Kombinations-Gerät. Die entsprechende Schaltung zur Messung induktiver
Blindleistung zeigt das Bild. Was gemessen werden soll, nämlich
wird mit den um 90° nacheilenden Spannungen messbar als
Dreileiter-Stromkreis
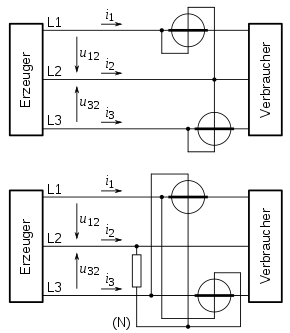
Durch den fehlenden Neutralleiter im Dreileiter-Stromkreis ist
Wie im Artikel zur Wirkleistung gezeigt wird, kann ein Strom, hier ,
herausgerechnet werden, und es reichen zwei Leistungsmesser in Aronschaltung aus. Das
zugehörige Bild zeigt die Messschaltungen für Wirk- und Blindleistung. Beide
sind für beliebige Belastung geeignet. Die Rechnung für die Wirkleistung ergibt
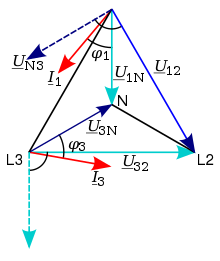
Zum Anschluss der um 90° nacheilenden Spannungen ist im Dreileiter-Stromkreis
das Neutralleiter-Potential durch einen Sternpunkt gemäß Bild künstlich zu
schaffen mit einem Widerstand, der genauso groß ist wie der Widerstand des
Spannungspfades in den Leistungsmessern. Da die gedrehten Spannungen hier um den
Faktor
kleiner sind, müssen die Messwerte um den Faktor
vergrößert werden (mit Spannungswandler oder durch Rechnung), und es ergibt sich
wobei
= Winkel zwischen
und
und
= Winkel zwischen
und
.
Die Einzelmesswerte der beiden Messgeräte haben keine anschauliche Bedeutung,
nicht einmal im Vorzeichen. Wenn
kleiner wird als 30°, wird der zweite Summand negativ; ein korrekter Anschluss
für im Vorzeichen richtiges Messen ist erforderlich.
Symmetrische Belastung
Bei symmetrischer Belastung reicht die Verwendung nur eines Leistungsmessers für den Leistungs-Bezug durch einen der Außenleiter. Die gesamte Leistung ist davon das Dreifache.
Daraus wird mit der gedrehten Spannung
wobei
= Winkel zwischen
und
Siehe auch
Literatur
- Réne Flosdorff, Günther Hilgarth: Elektrische Energieverteilung. 4. Auflage, Teubner, Stuttgart 1982, ISBN 3-519-36411-5.
- Horst Bumiller u.a. (Hrsg.): Fachkunde Elektrotechnik. 29. Auflage, Europa-Lehrmittel, Haan-Gruiten 2014, ISBN 978-3-8085-3190-7.
- Horst Stöcker (Hrsg.): Taschenbuch der Physik. 6. Auflage, Harri Deutsch, Frankfurt am Main 2010, ISBN 978-3-8171-1861-8; 7. Auflage. Europa-Lehrmittel, Haan-Gruiten 2014, ISBN 978-3-8085-5677-1
- Günter Springer: Rechenbuch Elektrotechnik. 11. verbesserte Auflage, Europa-Lehrmittel, Haan-Gruiten 1992, ISBN 3-8085-3371-4.
Anmerkungen
- ↑
Die Grafik bildet eine Periode der Spannung und
der Stromstärke ab, d. h. einen
Bereich mit der Länge
. Die
-Achse ist nicht mit Werten beschriftet, weil das Bild für jeden Sinus- oder Kosinusansatz gilt.
- ↑
Die Basisfunktionen des Ansatzes
und
sind wegen
zueinander orthogonal.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.12. 2021