Verzerrungsblindleistung

Die Verzerrungsblindleistung ist ein Begriff aus der Elektrotechnik und beschreibt eine spezielle Form der Blindleistung, die in Wechsel- bzw. Drehstromnetzen durch nichtlineare Verbraucher verursacht wird. Neben der hier verwendeten genormten Bezeichnung kommen in der Literatur alternativ die Begriffe Verzerrungsleistung, Oberschwingungsblindleistung oder Oberwellenblindleistung vor.

Allgemeines

Stromversorgungsnetze werden fast immer mit sinusförmiger Wechselspannung betrieben. Daher hat bei linearen elektrischen Bauelementen wie ohmschen Widerständen oder sogenannten Blindwiderständen der Strom ebenfalls einen sinusförmigen Verlauf. Sind Strom und Spannung sinusförmig, tritt keine Verzerrungsblindleistung auf. Verzerrungsblindleistung kann es immer nur dann geben, wenn ein nichtsinusförmiger Strom oder eine nichtsinusförmige Spannung vorhanden sind. Bei elektrischen Verbrauchern, die Verzerrungsblindleistung erzeugen, kann meistens von einer sinusförmigen Spannung (wird durch das Versorgungsnetz bereitgestellt) und einem verzerrten, nicht sinusförmigen Strom ausgegangen werden.

Die Ursache für den nichtsinusförmigen Strom und die Verzerrungsblindleistung sind nichtlineare elektrische Baugruppen, wie Gleichrichter in Netzteilen, Wechselrichter oder auch magnetische Bauteile, die magnetische Sättigungserscheinungen zeigen. Diese Baugruppen verursachen Verzerrung zu nichtsinusförmigen Wechselströmen. Deren Verlauf kann durch eine Fourierreihe als eine Summe aus Grundschwingung und Oberschwingungen dargestellt werden. Diese Oberschwingungen des Stromes in Kombination mit der sinusförmigen Netzspannung ergeben einen Anteil zur Gesamtblindleistung.

Die auftretenden Oberschwingungen sind fast immer unerwünscht, da sie das Netz belasten und am Verbraucher keine Arbeit verrichten können. Ebenfalls sind sie auch oft die Ursache von elektromagnetischen Störungen. Durch den Einsatz von Leistungsfaktorkorrekturfiltern kann der Anteil an Oberschwingungen reduziert werden.

Neben der Verzerrungsblindleistung kann Verschiebungsblindleistung auftreten.

Berechnung

Zusammenhang der verschiedenen Leistungsangaben

Die Wirkleistung ist die Leistung, die an einem Verbraucher in der Lage ist, Arbeit zu verrichten, beispielsweise eine Drehbewegung gegen ein Drehmoment beim Elektromotor oder die Temperatursteigerung bei einer Elektroheizung. Wirkleistung ergibt sich in oberschwingungsbehafteten Systemen nur aus Schwingungsanteilen von Strom und Spannung, die zueinander proportional sind. Wenn die Spannung keine Oberschwingungsanteile besitzt, tragen Oberschwingungen insgesamt zur Wirkleistung nichts bei (siehe auch unter Wirkstrom).

Nur die Grundschwingung des Stromes generiert also mit der (Grundschwingung der) Spannung Wirkleistung und gegebenenfalls Verschiebungsblindleistung . Diese tritt dann auf, wenn die beiden Schwingungen in der Phase verschoben sind. Die Grundschwingungsscheinleistung $S_{1}$ ist die pythagoräische Summe aus Wirkleistung und Verschiebungsblindleistung:

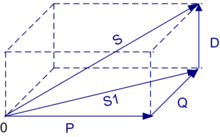
Zeigerdiagramm der Wirkleistung , Verschiebungsblindleistung und Verzerrungsblindleistung

$S_1 = \sqrt{P^2 + Q^2}\ .$

Zur Scheinleistung kommt als dritte Komponente die Verzerrungsblindleistung aus den Oberschwingungen hinzu. Ist der Effektivwert der Spannung, $I_{1}$ der Effektivwert des Grundschwingungsstromes, und sind $I_{2},\;I_{3},\;I_{4}$ usw. die Effektivwerte der Oberschwingungsströme, so lassen sich der Gesamtstrom und der Verzerrungsblindstrom $I_{\mathrm {v} }$ als

$I={\sqrt {\sum _{i=1}^{\infty }I_{i}^{2}}}\quad$ und $\quad I_{\mathrm {v} }={\sqrt {\sum _{i=2}^{\infty }I_{i}^{2}}}$

ausdrücken und die Verzerrungsblindleistung als

$D = U I_{\mathrm v} = U \cdot \sqrt{\sum^\infty_{i=2}I_i^2}\,.$

Die Gesamtblindleistung $Q_{\mathrm {ges} }$ – in der Abbildung nicht explizit dargestellt – ergibt sich aus der Verschiebungsblindleistung und der Verzerrungsblindleistung zu

$Q_\mathrm{ges} = \sqrt{Q^2 + D^2}\,.$

Die gesamte Scheinleistung ist im allgemeinen Fall gegeben durch

$S = U\cdot I= \sqrt {P^2 + Q^2 + D^2}\,.$

In der Abbildung ist das Zeigerdiagramm mit den Zeigern für die verschiedenen Leistungen dargestellt.

Die Größen $U,\,I,\,P$ und sind messbar, siehe Effektivwertmessung, Wirkleistungsmessung, Blindleistungsmessung.

Zusammenhang mit dem Klirrfaktor

Der Klirrfaktor oder Oberschwingungsgehalt einer oberschwingungsbehafteten Größe ist ein Maß für die Verzerrung und für den Anteil der Verzerrungsblindleistung in elektrischen Systemen. Der Klirrfaktor beschreibt das Verhältnis der pythagoräischen Summe der Effektivwerte $I_{2},I_{3},I_{4},\dots$ des Oberschwingungsspektrums zur pythagoräischen Summe der Effektivwerte des Gesamtspektrums $I_{1},I_{2},I_{3},I_{4},\dots$ inklusive des Grundschwingungsanteils $I_{1}$ . Unter der Voraussetzung, dass die Spannung rein sinusförmig ist und der Strom keinen Gleichanteil besitzt, lässt sich die Verzerrungsblindleistung mit dem Klirrfaktor des Stromes

$k = \frac{\sqrt{\sum^\infty_{i=2}I_i^2}}{\sqrt{\sum^\infty_{i=1}I_i^2}}=\frac{\sqrt{I_2^2+I_3^2+I_4^2+\dots}}{\sqrt{I_1^2+I_2^2+I_3^2+I_4^2+\dots}}$

und der Scheinleistung ausdrücken durch

$D = k \cdot S\,.$

Als Alternative zum Oberschwingungsgehalt wird gelegentlich der Grundschwingungsgehalt genannt. Numerische Angaben dieser Größe sind in Blick auf den Anteil der Verzerrungsblindleistung häufig wenig hilfreich, da beispielsweise der Bereich $D/S$ = 0 … 14 % beim Grundschwingungsgehalt durch den Bereich 100 … 99 % abgedeckt wird.

Beispiele

Bei linearen Blindwiderständen wie idealen Kondensatoren oder Induktivitäten tritt keine Verzerrungsblindleistung auf, sondern ausschließlich die Verschiebungsblindleistung.
Schaltet man zu einem ohmschen Lastwiderstand, z. B. einer Heizplatte, eine Diode in Serie, so werden der Quelle einer sinusförmigen Wechselspannung neben einem Grundschwingungsstrom auch Gleichstrom und Oberschwingungsströme entnommen. An der Quelle tritt neben der Wirkleistung auch Verzerrungsblindleistung auf. Quantitative Rückschlüsse aufgrund des Klirrfaktors sind wegen des Gleichstromanteils in der Scheinleistung nicht möglich.

Allerdings ist eine Lösung möglich, wenn man die Fourier-Koeffizienten berechnet. Bezeichnet man den ohne die Diode fließenden Strom mit $I_{0}$ , so lässt sich anhand der Koeffizienten rechnen:

$I_{\mathrm {gl} }={\frac {\sqrt {2}}{\pi }}I_{0}\;;\qquad I_{1}={\frac {1}{2}}I_{0}\;.$ Weitere ungeradzahlige Harmonische treten nicht auf.

$I_2=\frac1\pi \frac2{1\cdot3}I_0\;; \quad I_4=\frac1\pi \frac2{3\cdot5}I_0\;; \quad I_6=\frac1\pi \frac2{5\cdot7}I_0\;; \quad \ldots$

$I_{\mathrm v}^2=I_2^2+I_3^2+\dotsb =0{,}0473\;I_0^2$

$I^{2}=I_{\mathrm {gl} }^{2}+I_{1}^{2}+I_{2}^{2}+I_{3}^{2}+\dotsb$ $=0{,}4999\;I_0^2\;;$ theoretisch exakt $=\frac12\;I_0^2\;,$ siehe unter Scheinleistung.

$\frac{D^2}{S^2} =\frac{I_{\mathrm v}^2}{I^2} =0{,}0946; \quad D=30{,}8\,\%\cdot S$

Zur Verzerrungsblindleistung bei Verwendung eines Dimmers, siehe ebenfalls unter Scheinleistung.

Oberschwingungsanteile bei verschiedenen Verbrauchern

In folgender Tabelle sind verschiedene Verbraucher und deren Oberschwingungsverteilung ohne Filterung bei Betrieb an sinusförmiger Wechselspannung aufgelistet. Die Oberschwingungsströme sind relativ zur Grundschwingung des Stromes angegeben. Dabei gilt allgemein: Je höher die Oberschwingungsanteile im Strom desto höher die Verzerrungsblindleistung der betreffenden Verbraucher.

Ursache von Oberschwingungsströmen und der Verzerrungsblindleistung
Ursache	Kennlinie	Beispielhafter Verbraucher	$I_{n}/I_{1}$ in %
Ursache	Kennlinie	Beispielhafter Verbraucher	n=2	n=3	n=4	n=5	n=7
Keine. Es treten keine Oberschwingungen auf		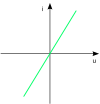Heizplatte	0	0	0	0	0
magnetische Sättigung		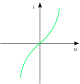Transformator mit unterdimensionierten Kern	0	25…55	0	8…30	2…10
Gasentladung, Glimmentladung		Leuchtstofflampe	1…2	8…20	0	2…3	1…2
Einweggleichrichter mit ohmscher Last ohne Glättungskondensator		Leistungshalbierung thermischer Geräte wie Haarfön	42	0	8	0	0
Einweggleichrichter mit kapazitiver und ohmscher Last, mit Glättungskondensator		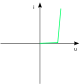Einfache Kleinstnetzteile Unterhaltungselektronik	70…90	40…60	30…50	25…50	12…25
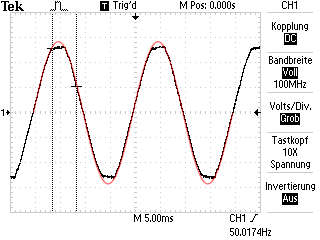
Vollweggleichrichter mit kapazitiver und ohmscher Last, mit Glättungskondensator		Netzteile in PCs, Druckern, Monitor, TV	0	65…80	0	50…70	25…35

Auswirkungen

Besonders im Konsumgüterbereich ist es in den letzten Jahren zu einem Anwachsen von Verbrauchern gekommen, die netzseitig einen Gleichrichter haben und somit Verzerrungsblindleistung erzeugen. Dazu gehören z.B. Energiesparlampen und Netzteile für Computer, Ladegeräte für Akkumulatoren, Monitore, TV-Geräte usw. Abhilfe schafft ein Leistungsfaktorkorrekturfilter (PFC), üblicherweise als sogenannter aktiver Leistungsfaktorkorrekturfilter ausgeführt.

Da die Verzerrungsblindleistung vom Netz übertragen werden muss, kommt es zu einer stärkeren Beanspruchung des elektrischen Versorgungsnetzes und Störungen wie Flicker. Im Gegensatz zu den Strömen der Grundschwingung heben sich die Ströme der durch drei teilbaren Oberschwingungen im Neutralleiter eines Dreiphasenwechselstromnetzes nicht auf, sondern addieren sich. Dies betrifft bei der in Europa üblichen Netzfrequenz von 50 Hz insbesondere die dritte Harmonische mit 150 Hz und die neunte Harmonische mit 450 Hz. Dadurch kann es, insbesondere wenn der Neutralleiter mit deutlich geringerem Querschnitt als die Außenleiter ausgeführt ist, zu einer unzulässig hohen Strombelastung am Neutralleiter kommen.

Die Grenzwerte der Oberschwingungsanteile in Prozent relativ zur Nennspannung in öffentlichen Niederspannungsnetzen (230 V zwischen Außenleiter und Neutralleiter) und im Mittelspannungsnetz (zwischen zwei beliebigen Außenleitern mit 10 kV bzw. 20 kV) sind festgelegt zu:

Gemessener Verlauf der Netzwechselspannung an einer Transformatorenstation zufolge einer Vielzahl von nichtlinearen Kleinverbrauchern. Deutlich erkennbar die Abflachung der Spannung im Bereich der Maximalwerte. Zum Vergleich in hellen Rot der sinusförmige Verlauf

Grenzwerte gemäß DIN EN 50160
Ungerade Harmonische				Gerade Harmonische
Nichtvielfache von 3		Vielfache von 3
Ordnung	%U_Nenn	Ordnung	%U_Nenn	Ordnung	%U_Nenn
5	6,0 %	3	5,0 %	2	2,0 %
7	5,0 %	9	1,5 %	4	1,0 %
11	3,5 %	15	0,5 %	6 ≤ n ≤ 24	0,5 %
13	3,0 %	21	0,5 %
17	2,0 %
19	1,5 %
23	1,5 %
25	1,5 %

Literatur

Flosdorff, Hilgarth: Elektrische Energieverteilung, Teubner Verlag, 2003, ISBN 3-519-26424-2
Budeanu, Constantin: Puissances reactives et fictives 1927

Basierend auf einem Artikel in:

Wikipedia.de