
Fluchtgeschwindigkeit (Raumfahrt)
Bei der Fluchtgeschwindigkeit (oder Entweichgeschwindigkeit) reicht die kinetische Energie eines Probekörpers (z.B. einer Rakete) gerade aus, um dem Gravitationspotential eines Himmelskörpers ohne weiteren Antrieb (ballistisch) zu entkommen. Tabellierte Werte beziehen sich meist auf die Oberfläche von Himmelskörpern als Ausgangspunkt. Nicht berücksichtigt werden ggf. Luftreibung, der Geschwindigkeitsbeitrag durch die Rotation des Körpers und Beiträge anderer Himmelskörper zum Gravitationspotential. Die Fluchtgeschwindigkeit hängt nach dem Schalentheorem für einen kugelsymmetrischen Körper lediglich von dessen Masse und Radius ab.
Die Fluchtgeschwindigkeit von der Erde heißt auch zweite kosmische Geschwindigkeit – die erste ist die Kreisbahngeschwindigkeit im niedrigen Orbit. Der Begriff kosmische Geschwindigkeit mit der Bedeutung sehr großer Geschwindigkeit entstand in der Mitte des 19. Jahrhunderts im Zusammenhang mit Meteoren. Zur Zeit des Wettlaufs zum Mond wurden die kosmischen Geschwindigkeiten gelegentlich auch astronautisch genannt.
Kreisbahngeschwindigkeit
Wenn sich ein Körper mit der Geschwindigkeit
auf einer Kreisbahn mit Radius
um das Zentrum der Erde (oder eines anderen Himmelskörpers) bewegt, beträgt
seine Zentripetalbeschleunigung
.
Im freien Fall wird sie
ausschließlich von der Gravitation des Planeten verursacht, also:
Dabei ist
die Gravitationskonstante
und
die Masse des Planeten. Die Kreisbahngeschwindigkeit ergibt sich durch Umstellen
der obigen Gleichung zu:
Für die Erde ist
3,986·1014 m3/s2 und der mittlere Radius
6371 km. Damit ergibt sich die Kreisbahngeschwindigkeit als erste
kosmische Geschwindigkeit zu
= 7,91 km/s.
In etwa 180 km Höhe, also etwa an der Grenze der Erdatmosphäre, beträgt die Kreisbahngeschwindigkeit etwa 7,8 km/s.
Schon beim Raketenstart trägt die Erdrotation zur Kreisbahngeschwindigkeit bei, beim Start am Äquator in Richtung Osten ist dieser Beitrag etwa 0,46 km/s. Die erforderliche Energie sinkt um mehr als 10 %.
Fluchtgeschwindigkeit
| Himmels- körper |
in km/s |
|---|---|
| Merkur | 4,3 |
| Venus | 10,2 |
| Erde | 11,2 |
| Mond | 2,3 |
| Mars | 5,0 |
| Jupiter | 59,6 |
| Saturn | 35,5 |
| Uranus | 21,3 |
| Neptun | 23,3 |
| Pluto | 1,1 |
| Sonne | 617,3 |
| Sonne im Erdabstand |
42,0 |
Die Fluchtgeschwindigkeit ist die Mindestgeschwindigkeit für eine offene, nicht zurückkehrende Bahn. Die kinetische Energie eines Probekörpers ist dann gleich seiner Bindungsenergie im Gravitationsfeld, also:
Umstellen nach
ergibt:
Die Fluchtgeschwindigkeit ist also um den Faktor
größer als die erste kosmische Geschwindigkeit.
Für Himmelskörper mit konstanter mittlerer Dichte
und Radius
skaliert
mit
,
also linear mit
.
Nebenstehende Tabelle enthält Beispiele.
Alternative Berechnung der Fluchtgeschwindigkeit aus der
Oberflächengravitationsbeschleunigung g und dem Radius des Objektes
ohne Berücksichtigung der Rotationsgeschwindigkeit des Objektes:
In dem Wert 11,2 km/s für die Erde, der zweiten kosmischen
Geschwindigkeit, ist wieder die Rotationsgeschwindigkeit der Erde nicht
berücksichtigt. Auch muss für Flugbahnen zum Mond
die Fluchtgeschwindigkeit nicht vollständig erreicht werden, denn L1 liegt nicht bei
.
Bei den Apollo-Missionen
betrug die Geschwindigkeit beim Wiedereintritt 10,8 km/s.
Geometrische Bedeutung
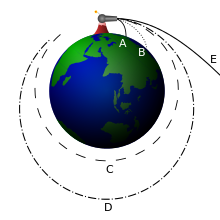
Wenn ein Flugkörper, der sich auf einer Kreisbahn um einen Planeten befindet, einen Geschwindigkeitsschub in Flugrichtung erhält, so verformt sich seine Flugbahn zu einer Ellipse. Wird die Geschwindigkeit weiter erhöht, steigt die Exzentrizität der Ellipse an. Das geht so lange, bis der ferne Brennpunkt der Ellipse unendlich weit weg ist. Ab dieser Geschwindigkeit ist der Körper nicht mehr auf einer geschlossenen Bahn, sondern die Ellipse öffnet sich zu einer Parabelbahn. Dies geschieht genau dann, wenn der Flugkörper die zweite kosmische Geschwindigkeit erreicht.
Während sich der Körper von dem Planeten entfernt, wird er von dessen Gravitation weiterhin abgebremst, sodass er erst in unendlicher Entfernung zum Stillstand kommt. Wird hingegen die zweite kosmische Geschwindigkeit überschritten, so nimmt die Flugbahn die Form eines Hyperbel-Asts an – in diesem Fall bleibt im Unendlichen eine Geschwindigkeit übrig, die als hyperbolische Exzessgeschwindigkeit oder hyperbolische Überschussgeschwindigkeit bezeichnet wird und die Energie der Hyperbelbahn charakterisiert. Sie berechnet sich aus der Summe der Energien, also der Quadrate der Geschwindigkeiten, analog zur Berechnung im Folgeabschnitt. Ebenfalls üblich ist die Angabe des Quadrates der Geschwindigkeit (also Energie pro Masse), häufig mit dem Formelzeichen c3.
Fluchtgeschwindigkeit von einem Schwarzen Loch
In der allgemeinen
Relativitätstheorie berechnet sich die radiale Fluchtgeschwindigkeit wie
nach Newton, ist aber richtungsabhängig. Zudem ist die Kreisbahngeschwindigkeit
höher als nach Newton, um den Faktor ,
mit
.
Erst mit steigendem Abstand vom Schwerpunkt konvergiert das Verhältnis von
Flucht- und Kreisbahngeschwindigkeit gegen
.
Das hat seinen Grund darin, dass im Gravitationsfeld der Raum nicht euklidisch
ist und der Umfang eines Kreises weniger als
beträgt. Während die Fluchtgeschwindigkeit erst am Ereignishorizont des
schwarzen Loches, bei
,
die Lichtgeschwindigkeit
erreicht, ist die Kreisbahngeschwindigkeit schon bei
(an der sogenannten Photonensphäre) gleich
und bis
größer als die radiale Fluchtgeschwindigkeit
Fluchtgeschwindigkeiten von weiteren Objekten
Als dritte kosmische Geschwindigkeit
gilt die minimale Startgeschwindigkeit von der Erdoberfläche, mit der (bei
Ausnutzen der Bahngeschwindigkeit der Erde um die Sonne, aber ohne Ausnutzen
ihrer Eigenrotation und ohne Swing-by-Manöver
an Planeten) das Sonnensystem verlassen werden kann. Der Flugkörper muss also
das gemeinsame Gravitationsfeld von Erde und Sonne überwinden. Nach dem
Start mit
= 11,2 km/s und Verlassen der Einflusssphäre der
Erde hat der Körper noch die hyperbolische Exzessgeschwindigkeit
.
Diese muss zusammen mit der Bahngeschwindigkeit
der Erde die Fluchtgeschwindigkeit
aus dem Sonnensystem im Abstand
= 1 AE
ergeben,
.
Die zum Erreichen dieser Geschwindigkeit nötige Startgeschwindigkeit
ergibt sich dann aus
bzw.
.
Die Masse des Mondes und der anderen Planeten ist hier vernachlässigt worden; das Ergebnis würde sich kaum ändern.
Im Fall der Fluchtgeschwindigkeit aus der Milchstraße
ist das Gravitationsfeld jedoch sehr deutlich kein Zentralfeld und ein
beträchtlicher Teil der Masse liegt außerhalb der Bahn der Sonne um das
galaktische Zentrum. Eine numerische Berechnung, die auch ein Modell für die
Verteilung der Dunklen
Materie berücksichtigt, ergibt eine Fluchtgeschwindigkeit von .
Das ist erwartungsgemäß weit mehr als das
-fache
der Bahngeschwindigkeit der Sonne von rund 220 km/s.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.11. 2019