Elastizitätsmodul

Name

E-Modul

Größen- und Einheitensystem	Einheit	Dimension
SI	Pa = N/m² = kg·m⁻¹·s⁻²	M·L⁻¹·T⁻²
cgs	Ba = dyn/cm² = cm⁻¹·g·s⁻²

Siehe auch: Spannung (Mechanik) $\sigma$ Druck p

Der Elastizitätsmodul, auch, E-Modul, Zugmodul, Elastizitätskoeffizient, Dehnungsmodul, oder Youngscher Modul, ist ein Materialkennwert aus der Werkstofftechnik, der bei linear-elastischem Verhalten den proportionalen Zusammenhang zwischen Spannung und Dehnung bei der Verformung eines festen Körpers beschreibt. Der Elastizitätsmodul – in anderer Notation direkt proportional zur Federkonstante – ist die Proportionalitätskonstante im Hookeschen Gesetz.

Die Größenart des Elastizitätsmoduls ist die mechanische Spannung. Als Formelzeichen ist üblich.

Der Elastizitätsmodul wächst mit dem Widerstand, den ein Material seiner elastischen Verformung entgegensetzt. Ein Bauteil aus einem Material mit hohem Elastizitätsmodul wie Stahl ist somit steifer als das gleiche Bauteil aus einem Material mit niedrigem Elastizitätsmodul wie Gummi.

Bei anisotropen, insbesondere bei kristallinen Materialien ist der Elastizitätsmodul richtungsabhängig und muss durch den Elastizitätstensor beschrieben werden, dessen Komponenten vereinfacht durch die elastischen Konstanten dargestellt werden. Diese sind Materialkonstanten, die innerhalb realer Festkörper variieren, da reale Festkörper weder perfekt homogen sind (insbesondere Beton) noch konstante physikalische Eigenschaften (z.B. Temperatur) haben.

Definition

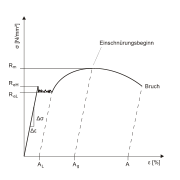
Schematisches Spannungs-Dehnungs-Diagramm: für kleine Dehnungen linear, Hookesche Gerade mit Steigung E

Der Elastizitätsmodul ist als Steigung des Graphen im Spannungs-Dehnungs-Diagramm bei einachsiger Belastung bei infinitesimaler Verzerrungsänderung bei Spannungsfreiheit definiert. Die meisten Materialien haben einen (zumindest kleinen) linearen Bereich, dieser wird auch als Hookescher Bereich bezeichnet.

$E={\frac {\sigma }{\varepsilon }}={\text{const.}}$

Dabei bezeichnet $\sigma ={\frac {F}{A}}$ die mechanische Spannung Kraft pro Fläche (Normalspannung, nicht Schubspannung) und $\varepsilon ={\frac {\Delta \ell }{\ell _{0}}}$ die Dehnung. Die Dehnung ist das Verhältnis von Längenänderung $\Delta \ell =\ell -\ell _{0}$ zur ursprünglichen Länge $\ell _{0}$ . Die Einheit des Elastizitätsmoduls ist die einer Spannung:

$\left[E\right]=1\,{\frac {\mathrm {N} }{\mathrm {mm} ^{2}}}=1\,\mathrm {MPa}$ , in SI-Einheiten: $\left[E\right]=1\,{\frac {\mathrm {N} }{\mathrm {m} ^{2}}}=1\,\mathrm {Pa}$ .

Der Elastizitätsmodul wird als Materialkonstante bezeichnet, da mit ihm und den Querkontraktionszahlen das Elastizitätsgesetz aufgestellt wird. Der Elastizitätsmodul ist aber nicht bezüglich aller physikalischen Größen konstant. Er hängt von verschiedenen Umgebungsbedingungen wie z.B. Temperatur oder Feuchte ab.

Anwendung

Bei ideal linear-elastischem Werkstoffgesetz (Proportionalitätsbereich im Spannungs-Dehnungs-Diagramm) ergibt sich die Federkonstante c eines geraden Stabes aus seiner Querschnittsfläche A, seiner Länge $L_{0}$ und seinem Elastizitätsmodul E:

$c={\frac {F}{\Delta L}}={\frac {E\cdot A}{L_{0}}}$ .

Mit den Ausdrücken $\sigma ={\frac {F}{A}}$ für die Spannung und $\varepsilon ={\frac {\Delta L}{L_{0}}}$ für die Dehnung erhält man aus obiger Gleichung das Hookesche Gesetz für den einachsigen Spannungszustand

$\sigma =E\cdot \varepsilon$

und daraus den E-Modul

$E={\frac {\sigma }{\varepsilon }}$

Typische Zahlenwerte

Material	E-Modul in GPa	Material	E-Modul in GPa
Metallische Werkstoffe bei 20 °C		Nichtmetallische Werkstoffe bei 20 °C
Beryllium	303	PVC	1,0 … 3,5
Baustahl	210	Glas	40 … 90
V2A-Stahl	180	Beton	20 … 40
Gusseisen	90 … 145	Keramik	160 … 440
Messing	78 … 123	Holz	10 … 15
Kupfer	100 … 130	Polypropylen	1,3 … 1,8

Beziehungen elastischer Konstanten

Es bestehen verschiedene Zusammenhänge zwischen Elastizitätsmoduln gemäß denen für isotrope Materialien ein Elastizitätsmodul aus zwei anderen berechnet werden kann.

Neben dem Elastizitätsmodul (E-Modul) wird der Schubmodul, auch Scher- oder G-Modul genannt, verwendet, der bei Schub gemessen wird und je nach Querkontraktionszahl für nicht-auxetische Materialien das 0,33- bis 0,5fache des Elastizitätsmoduls beträgt. Bei steifen Materialien wird meistens der Elastizitätsmodul gemessen, bei weichen (Gele, Polymer-Schmelzen) der Schubmodul, da sich der Elastizitätsmodul bei solchen Systemen meist nicht mehr gut messen lässt, weil sich die Probe unter ihrem eigenen Gewicht verformt (das sog. Sagging).

Es gilt für ein linear-elastisches, isotropes Material folgender Zusammenhang zwischen dem Schubmodul G, dem Kompressionsmodul K und der Poissonzahl $\nu$ :

$E=2(1+\nu )\cdot G=3(1-2\nu )\cdot K={\frac {9KG}{3K+G}}$

Bezug zu anderen Eigenschaften metallischer Werkstoffe

Der E-Modul hat keinen strengen Bezug zur Härte sowie zu Streckgrenze $R_{e}$ und Zugfestigkeit $R_{m}$ metallischer Werkstoffe (z.B. einfacher Baustahl und hochfester Sonderstahl). Der E-Modul eines Metalls steigt mit seiner Schmelztemperatur. Zudem besitzen kubisch raumzentrierte Metalle bei vergleichbarer Schmelztemperatur einen höheren E-Modul als kubisch flächenzentrierte. Der Zusammenhang auf atomarer Ebene ergibt sich aus der Bindungsstärke der Atome im Kristallgitter.

Spannungen und Dehnungen in statisch (un)bestimmten Systemen

In statisch bestimmten Systemen ergeben sich die mechanischen Spannungen im linear-elastischen Bereich aus der Last (einwirkende Kräfte) und der Geometrie, während die Dehnungen vom E-Modul der Werkstoffe abhängen. Verformt sich das Material plastisch, so werden Spannungen dadurch begrenzt.

In Fällen statischer Unbestimmtheit (z.B. Durchlaufträger, behinderte Wärmedehnung, Schiffsrumpf im Wellengang oder im Tidenhub) sind die wirkenden Kräfte und induzierten Spannungen abhängig von der Steifigkeit des statischen Systems. In solchen Fällen können Bauteile aus nachgiebigeren Werkstoffen mit niedrigerem Elastizitätsmodul bewirken, dass Spannungen geringer ausfallen. Die Bauteile passen sich flexibler den Gegebenheiten an. Steifere Werkstoffe hingegen widersetzen sich in höherem Maße der elastischen Verformung, wodurch sich größere Spannungen aufbauen.

E-Modul versus Steifigkeit

Der Begriff Steifigkeit im Sinne der Technischen Mechanik beschreibt allgemein den Widerstand von Körpern oder Baugruppen gegen elastische Verformung durch mechanische Kräfte oder Momente. Ihr Wert ergibt sich somit nicht allein aus den elastischen Eigenschaften der verwendeten Materialien, sondern wird ebenfalls durch die jeweilige Körpergeometrie bzw. Konstruktion (z.B. Maschinensteifigkeit) bestimmt. Im Falle des Zugversuches ist die Zug- bzw. Dehnsteifigkeit der Probe das Produkt aus deren (effektiven) E-Modul sowie der kleinsten orthogonal belasteten Querschnittsfläche :

$S_{\mathrm {t} }=E\cdot A$ .

Die physikalische Einheit entspricht hierbei der einer Kraft.

Der Begriff Steifigkeit im Sinne einer Werkstoffeigenschaft bezieht sich auf das Deformationsverhalten des Werkstoffes im elastischen Bereich. Hier entfällt die Geometrieabhängigkeit, weshalb allein die elastischen Materialkennwerte, z.B. E-Modul und Schubmodul zur Charakterisierung herangezogen werden.

Das Hookesche Gesetz in skalarer und allgemeiner Form

→ Hauptartikel: Hookesches Gesetz

→ Hauptartikel: Elastizitätstensor

Die Beziehung $\sigma =E\cdot \varepsilon$ in skalarer Schreibweise gilt nur für querdehnungsfreie Materialien oder für den einachsigen Spannungszustand (z.B. einachsiger Zug). Im mehrachsigen Spannungszustand muss das Hookesche Gesetz abhängig vom Grad der elastischen Anisotropie in seiner allgemeinen Form angewendet werden. So gilt beispielsweise für die laterale Verformung dünner isotroper Platten (ebener Spannungszustand)

$\left(\begin{array}{c} \sigma_{xx}\\ \sigma_{yy}\\ \sigma_{xy} \end{array}\right) = \frac{E}{1-\nu^2}\left(\begin{array}{ccc} 1& \nu & 0\\ \nu & 1& 0\\ 0& 0& \frac{1-\nu}{2} \end{array}\right) \left(\begin{array}{c} \varepsilon_{xx}\\ \varepsilon_{yy}\\ 2\varepsilon_{xy} \end{array}\right)$ ,

wobei $\nu$ die Poissonzahl bezeichnet. Die Dehnung in Dickenrichtung ergibt sich zu

$\varepsilon _{zz}=-{\frac {\nu }{E}}(\sigma _{xx}+\sigma _{yy})$ .

Bauteilversteifung durch biaxiale Spannungszustände

Beim Übergang vom einachsigen (uniaxialen) in den zweiachsigen (biaxialen) Spannungszustand können für Bauteile und Schichten aus homogenem isotropem Material zwei einfache Sonderfälle unterschieden werden. Dabei wird aufgrund der Beeinflussung der Querkontraktion für nicht-auxetische Materialien mit einer Poissonzahl echt größer Null stets ein höherer Modul in der Belastungsrichtung gemessen.

Infolge einer verhinderten Querkontraktion (ε_yy = 0) ergibt sich dieser zu

$E_{x}^{*}={\frac {E}{1-\nu ^{2}}}$ .

Liegt in Quer- bzw. y-Richtung zusätzlich eine Belastung in der Höhe σ_yy = σ_xx vor, so ist der „biaxiale E-Modul“

$E_{x}^{{**}}={\frac {E}{1-\nu }}$ .

Letzterer hat z.B. Bedeutung für die laterale Steifigkeit haftender Schichten, etwa bei Unterschieden im thermischen Ausdehnungsverhalten zwischen Schicht und Substrat. Der Erstgenannte kommt in dickwandigen Bauteilen oder sehr breiten Balken zum tragen. Die beiden abgeleiteten Größen sind jedoch keine Werkstoffkonstanten im ursprünglichen Sinn.

Siehe auch

Basierend auf einem Artikel in:

Wikipedia.de