Affine Translationsebene
Als affine Translationsebene oder kurz Translationsebene wird in der synthetischen Geometrie eine affine Ebene dann bezeichnet, wenn ihre Translationsgruppe scharf einfach transitiv auf ihr operiert und sie daher weitgehend durch diese Gruppe ihrer Translationen (Parallelverschiebungen) beschrieben werden kann, indem jedem Punkt der Ebene eine Translation zugeordnet wird. Der Endomorphismenring der Translationsgruppe, die bei einer Translationsebene stets kommutativ ist, enthält einen Schiefkörper, den Schiefkörper der spurtreuen Endomorphismen. Die Gruppe der Translationen ist ein Modul über diesem Schiefkörper.
Rein geometrisch ist eine affine Ebene genau dann eine Translationsebene, wenn in ihr der kleine affine Satz von Desargues (vergleiche die Abbildung am Ende der Einleitung) allgemeingültig ist, also ein Schließungssatz, der in der synthetischen Geometrie als Axiom verwendet wird.
Daneben wird in der synthetischen Geometrie seltener der Begriff projektive Translationsebene verwendet. Diese speziellen projektiven Ebenen hängen eng mit den affinen Translationsebenen zusammen. Dieser Zusammenhang wird im vorliegenden Artikel im Abschnitt Projektive Translationsebene erläutert. Die Begriffe affine Translationsebene bzw. projektive Translationsebene sind Verallgemeinerungen der Begriffe desarguessche affine bzw. desarguessche projektive Ebene.
Die Untersuchung der Translationen und ihrer spurtreuen Endomorphismen ist neben der Beschreibung durch einen Koordinatenternärkörper eine gängige Methode, nichtdesarguesche Ebenen zu algebraisieren. Für desarguesche und erst recht für pappussche Ebenen fällt der Schiefkörper der spurtreuen Endomorphismen mit dem Koordinatenschiefkörper zusammen, bei Translationsebenen ist er im Koordinatenquasikörper als Kern enthalten.
Die Algebraisierung einer affinen Ebene mithilfe von Koordinaten auf einer Geraden der Ebene, algebraische Verknüpfungen dieser Koordinaten sowie die Begriffe Ternärkörper und Quasikörper, die im vorliegenden Artikel verwendet werden, sind in den entsprechenden Hauptartikeln ausführlicher dargestellt.
Definitionen und Eigenschaften
Translationen in affinen Inzidenzebenen
Eine bijektive Selbstabbildung
einer affinen Ebene
heißt Translation, wenn gilt
- das Bild jeder Geraden ist eine Gerade, d.h.
ist eine Kollineation
- für jede Gerade
der Ebene ist
,
ist fixpunktfrei oder die identische Abbildung der Ebene
,
.
Jede Translation
ist durch ein Punkt-Bildpunkt-Paar
eindeutig bestimmt.
Für nichtidentische Translationen ist die Verbindungsgerade
von
und
eine Spurgerade. Genau die Parallelen dieser Geraden bilden die Menge
aller Spuren von
.
Die Parallelenschar der Spuren
heißt Richtung der Translation
und man nennt
dann auch eine Verschiebung in Richtung
.
Translationsgruppe und spurtreue Endomorphismen
Die Menge der Translationen einer affinen Inzidenzebene bildet bezüglich der
Komposition
eine Gruppe .
Diese Gruppe ist kommutativ, falls es (nichtidentische) Translationen der Ebene
in (mindestens) zwei unterschiedliche Richtungen gibt. Ein Gruppenendomorphismus
heißt spurtreu,
wenn für jede nichtidentische Translation
die Spuren von
mit den Spuren von
übereinstimmen oder
der 0-Endomorphismus
ist. Gleichwertig:
ändert bei keiner Translation deren Richtung.
Ist die Translationsgruppe kommutativ und nichttrivial, [1]
dann wird die Menge
der spurtreuen Endomorphismen durch die Verknüpfungen
und
zu einem Ring
mit Nullement
und Einselement
,
einem Unterring des Endomorhismenringes. Die Reihenfolge, in der die
Homomorphismen in der Definition der Multiplikation auf Translationen angewendet
werden, bestimmt, ob die Translationsgruppe zu einem Links- oder Rechtsmodul
über
wird. Bei der hier gewählten Definition
und
für die „Skalarmultiplikation“ ist sie ein
-Linksmodul.
Affine Translationsebene
Eine affine Inzidenzebene heißt affine Translationsebene, wenn eine der folgenden äquivalenten Bedingungen zutrifft:
- Der kleine affine Satz von Desargues gilt in
.
- Der Koordinatenternärkörper, der
durch Wahl eines beliebigen Koordinatensystems zugeordnet werden kann, ist ein Quasikörper.
- Zu zwei Punkten
gibt es stets eine Translation
mit
.
- Die Translationsgruppe operiert scharf einfach transitiv auf
.
- Damit gibt es in einer affinen Translationsebene
, wenn man einen Punkt
als Ursprung fest wählt, eine natürliche Bijektion
zwischen den Punkten der Ebene und der Translationsgruppe. Eine Translationsebene kann so mit ihrer Translationsgruppe identifiziert werden.
- Andererseits kann jede Translation mit einer Äquivalenzklasse
von verschiebungsgleichen geordneten Punktepaaren („Pfeilen“) identifiziert
werden, dabei sind zwei Pfeile
äquivalent, wenn
und
mit derselben Translation
gilt. Man nennt diese Äquivalenzklassen von Pfeilen auch „Vektoren“.
Für die eindeutig bestimmte Translation, die einen Punkt
auf einen Punkt
abbildet, wird abkürzend
geschrieben. Diese Schreibweise bezeichnet zugleich die Äquivalenzklasse der zu
verschiebungsgleichen „Pfeile“.
Da bei einer Translationsebene jeder spurtreue Endomorphismus
sogar ein Gruppenautomorphismus ist, ist der Ring
hier sogar ein Schiefkörper. Die Gruppe der Translationen („Vektoren“ im oben
beschriebenen Sinn) bilden einen
-Linksmodul.
Lässt man als Skalarkörper eines Vektorraums
auch einen Schiefkörper zu, wie das gelegentlich in der Literatur geschieht, so
bildet die Gruppe der Translationen also tatsächlich einen
-Linksvektorraum.
Als Folge davon ist die Ordnung
jeder nichtidentischen Translation
durch die Charakteristik
von
bestimmt: Ist diese Charakteristik eine Primzahl
,
dann haben alle nichtidentischen Translationen diese Ordnung
,
ist sie 0, dann haben alle nichtidentischen Translationen unendliche Ordnung.
Genau dann, wenn die Charakteristik von 2 verschieden ist, erfüllt die
Translationsebene das (affine) Fano-Axiom.
Koordinatenquasikörper und spurtreue Endomorphismen
Kern des Koordinatenquasikörpers
Ein (Links-)Quasikörper unterscheidet sich von einem Schiefkörper dadurch,
dass kein Rechtsdistributivgesetz
und kein Assoziativgesetz
der Multiplikation gefordert wird. Definiert man für einen Quasikörper
als seinen Kern,
dann bildet dieser Kern einen Schiefkörper und dieser ist isomorph zum
Schiefkörper
der spurtreuen Endomorphismen von
zur Translationsebene
über
.
Über diesen Isomorphismus wird auch der Koordinatenquasikörper zu einem
-Linksmodul,
der zu dem Untermodul der Translationen in Richtung der ersten Koordinatenachse
in der Translationsgruppe
isomorph ist.
Hat man die Multiplikation in
als
definiert und die „Skalarmultiplikation“ von rechts als
dann muss für den Isomorphismus
die Multiplikation nicht umgekehrt werden, da die Elemente des Kerns nach
Konstruktion auch von rechts distributiv und assoziativ operieren und
wird dann zu einem
-Rechtsmodul.
Es ist aber in der Literatur üblich, nur Rechtsquasikörper – bei denen
die Definition des Kerns entsprechend angepasst werden muss – mit einer solchen
Rechtsmodulstruktur zu versehen, da sich bei „gleichseitiger“ Struktur
zwangloser eine geometrische Deutung von
als Gruppe von geometrischen Abbildungen ergibt.
Kommensurable Punkte, Streckungsfaktor, Teilverhältnis
Drei kollineare Punkte
der Translationsebene
nennt man kommensurabel,
wenn ein spurtreuer Endomorphismus
existiert, der die Translation, die
auf
verschiebt, in die Translation verwandelt, die
auf
verschiebt. Vektoriell geschrieben:
.
In diesem Fall nennt man
den Streckungsfaktor
zu dem Punktetripel
.
Aus dem Streckungsfaktor kann (für drei verschiedene kollineare und
kommensurable Punkte) umkehrbar eindeutig ein Teilverhältnis
gewonnen werden:
Die Bruchschreibweise
ist hier unproblematisch, da alle auftretenden Elemente von
untereinander kommutieren.
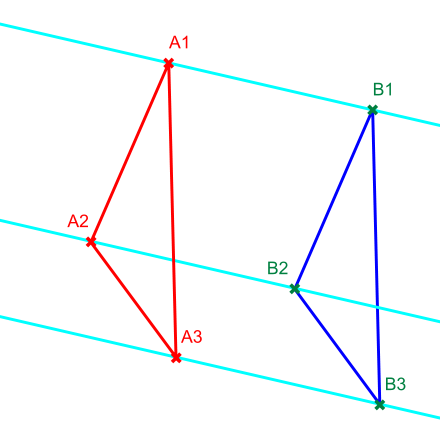
Strahlensatz und Streckungen

Sind
fünf Punkte einer affinen Translationsebene mit den Eigenschaften (vgl. die
Abbildung rechts):
sind nicht kollinear,
sind kollinear und kommensurabel,
sind kollinear,
dann gilt:
Dieser erste Strahlensatz für Translationsebenen rechtfertigt es, die
spurtreuen Endomorphismen als „Zentrische Streckungen“ der Translationsebene zu
bezeichnen und motiviert die Bezeichnung „Streckungsfaktor“: Wählt man einen
Ursprung
und ordnet wie oben ausgeführt jedem Punkt
die Translation
zu, dann operiert jeder „Streckungsfaktor“
auf den Punkten der Ebene als Kollineation
und sogar als Dilatation.
Bei dieser Dilatation ist der Ursprung Fixpunkt und alle Geraden durch den
Ursprung sind Fixgeraden. Umgekehrt operiert jede Dilatation, die genau den
Ursprung als Fixpunkt hat, durch Konjugation
auf den Translationen und diese Operation ist ein spurtreuer Endomorphismus der
Translationsgruppe. Daher sind bei einer Translationsebene die Untergruppe
der verallgemeinerten Streckungen mit Zentrum
und die Untergruppe der hier beschriebenen Streckungen um
mit einem Streckungsfaktor aus
identische Untergruppen der Affinitätengruppe.
Es folgt weiter: Sind in der oben dargestellten Konfiguration
und
Dreiecke,
und
jeweils kollinear und gilt
,
dann sind von den kollinearen Tripeln
entweder beide kommensurabel oder beide inkommensurabel. Sind sie
inkommensurabel, dann existiert keine Dilatation, die
als Fixpunkt hat und
auf
,
auf
abbildet. Damit kann auch keine Affinität mit dieser Eigenschaft existieren!
Da der Streckungsfaktor als Abbildung auf die Parallelverschiebungen wirkt,
ergibt sich unter den Voraussetzungen des ersten Strahlensatzes und der
zusätzlichen Voraussetzung
eine dem zweiten Strahlensatz entsprechende Aussage:
- diese Formel bleibt auch im Trivialfall
richtig. Die ersten beiden Strahlensätze
gelten also sinngemäß in jeder desargueschen Ebene, wobei dann die
Bedingung der Kommensurabilität entfallen kann, ganz allgemein, während der
dritte Strahlensatz, der in der synthetischen Geometrie auch
Dreistrahlsatz genannt wird, nur für pappussche Ebenen allgemein bewiesen
werden kann.
(Vergleiche die Hauptartikel Zentrische Streckung und Strahlensatz)
Desarguesche Ebenen
Eine Translationsebene
mit zugehörigem Schiefkörper der spurtreuen Endomorphismen
von
ist genau dann eine desarguesche Ebene, wenn eine der folgenden äquivalenten
Bedingungen zutrifft:
- Der große affine Satz von Desargues gilt in
.
- Ein Koordinatenquasikörper von
stimmt mit seinem Kern überein.
- Ein Koordinatenquasikörper von
ist ein Schiefkörper.
- Ein Koordinatenquasikörper von
ist isomorph zu
.
- Liegen drei Punkte der Ebene auf einer Geraden, so sind sie stets kommensurabel.
- Die Translationen bilden einen zweidimensionalen Linksvektorraum
über
.
Da die Koordinatenbereiche durch die affine Ebene bis auf Isomorphie eindeutig bestimmt sind, können die Aussagen über diese Bereiche „Ein Koordinatenquasikörper...“ hier gleichwertig auch mit „Jeder Koordinatenquasikörper...“ formuliert werden.
Andererseits enthält jede „echte“, also nichtdesarguesche Translationsebene
eine desarguesche Ebene als echte Teilmenge: Wählt man ein Koordinatensystem
und betrachtet nur Punkte mit Koordinaten
,
die zu
und
kommensurabel sind, und nur solche Geraden, deren Koeffizienten diese
Eigenschaft haben, dann erhält man eine zur desargueschen Ebene
isomorphe affine Inzidenzstruktur.
Pappussche Ebenen
Wenn sich in einer Translationsebene eine Orthogonalitätsrelation
definieren lässt und die Charakteristik
des Schiefkörpers
nicht 2 ist, das heißt, das (affine) Fano-Axiom
gilt, dann ist die Allgemeingültigkeit des Höhenschnittpunktsatzes und
des Mittellotensatzes äquivalent und – falls diese allgemeingültig sind –
ist in der Ebene der Satz
von Pappos allgemeingültig und der Koordinatenquasikörper sogar ein Körper.
(Siehe Präeuklidische
Ebene).
Allgemein erfüllt eine Translationsebene den Satz von Pappos genau dann,
- wenn sie desarguessch ist und die Multiplikation im Schiefkörper
der spurtreuen Endomorphismen der Translationsgruppe kommutativ ist, also
ein Körper ist oder gleichwertig
- wenn ihr Koordinatenquasikörper ein Körper ist.
Ist die Ordnung der Translationsebene endlich, dann ist der Schiefkörper
stets ein Körper. Dann ist die Translationsebene genau dann pappussch, wenn sie
desarguessch ist.
Endliche Ebenen
Eine affine oder projektive Ebene heißt endlich, wenn es ihre
Ordnung und damit auch die Anzahl der Punkte der Ebene ist. Die Ordnung
ist bei einer affinen Ebene die Anzahl der Punkte auf einer Geraden, bei einer
projektiven Ebene die Ordnung der affinen Ebene, die durch Schlitzen der
projektiven Ebene entsteht. Aus der Tatsache, dass der Koordinatenquasikörper
einer affinen Translationsebene ein Linksvektorraum über dem Schiefkörper
der spurtreuen Endomorphismen ist, ergeben sich zusammen mit dem Satz von
Wedderburn, der besagt, dass ein endlicher Schiefkörper stets kommutativ,
also ein endlicher Körper ist, Folgerungen für die endlichen
Translations- und Moufangebenen:
- Der Schiefkörper
einer endlichen Translationsebene ist ein endlicher Körper
, hat also
Elemente mit einer Primzahl
und
.
- Der Koordinatenquasikörper ist ein endlichdimensionarer Vektorraum über
und hat demnach
Elemente. Also ist die Ordnung der Translationsebene diese Primzahlpotenz, ist dabei
, dann ist die Translationsebene die pappussche Ebene
über dem Körper
.
- Es existieren zahlreiche endliche affine Translationsebenen, die nicht desarguesch sind, zum Beispiel 4 verschiedene (nicht isomorphe) der Ordnung 9. (Siehe die Beispiele im Artikel Ternärkörper.)
- Das formale Analogon zu affinen Translationsebenen unter den projektiven Ebenen sind die Moufangebenen, in denen der kleine projektive Satz von Desargues allgemeingültig ist. Ruth Moufang hat gezeigt, dass echte, das heißt nichtdesarguesche Moufangebenen stets unendlich sind. Daraus folgt, dass bei einer endlichen affinen Translationsebene die projektive Erweiterung genau dann eine Moufangebene ist, wenn beide Ebenen desarguesch und also gleichwertig dazu Ebenen über einem endlichen Körper sind.
Allgemeinere Aussagen über die möglichen Ordnungen endlicher Ebenen finden sich in den Artikeln Projektive Ebene und Projektive Geometrie.
Projektive Translationsebene
Eine projektive Ebene heißt Translationsebene bezüglich einer ihrer Geraden, wenn sie in Bezug auf diese Gerade als Achse den kleinen projektiven Satz von Desargues erfüllt. Eine gleichwertige Beschreibung einer solchen projektiven Translationsebene: Sie gehört zu einer der Klassen IVa, V oder VII in der Klassifikation projektiver Ebenen nach Hanfried Lenz.
Der projektive Abschluss einer affinen Translationsebene ist
stets eine projektive Translationsebene. Wenn andererseits eine projektive
Translationsebene entlang einer projektiven Geraden
geschlitzt wird, entsteht eine affine Ebene, in der diese Gerade die Ferngerade darstellt. Die so
erzeugte affine Ebene ist genau dann eine affine Translationsebene, wenn
die projektive Ebene den kleinen projektiven Satz von Desargues in Bezug auf
als Achse erfüllt. Gleichwertig: Die Gerade
muss eine Achse in der Lenz-Figur der projektiven Ebene sein.
Beispiele und Gegenbeispiele
- Jede desarguesche Ebene ist eine Translationsebene, also insbesondere die
affine Ebene
über einem Schiefkörper
. Hier stimmt der Schiefkörper der spurtreuen Endomorphismen
(bis auf Isomorphie) mit dem Koordinatenschiefkörper überein.
- Die reellen Oktonionen
bilden einen Quasikörper, der kein Schiefkörper ist: Zwar gelten beide Distributivgesetze, aber die Multiplikation ist nicht assoziativ. Damit ist die affine Translationsebene
eine nichtdesarguesche Translationsebene.
- Die reelle Moulton-Ebene
ist eine affine Ebene, die keine Translationsebene ist: Ist
die („normale“ und Moulton-Ebenen-) Gerade, auf der einige Moultongeraden ihren „Knick“ haben, dann besteht die Translationsgruppe genau aus den „normalen“ Verschiebungen der reellen Ebene in Richtung der Geraden
, sie ist damit zur kommutativen Gruppe
isomorph. Jeder Gruppenautomorphismus von
ist spurtreu, da aber die Translationsgruppe nicht einfach transitiv auf der Moulton-Ebene operiert, nützt das zur Beschreibung dieser Geometrie wenig.
- Dagegen sind die endlichen Moultonebenen stets affine Translationsebenen. Es existieren unendlich viele nichtdesarguesche endliche Translationsebenen dieses Typs, siehe dazu den Abschnitt Quasikörper endlicher Moulton-Ebenen im Artikel Quasikörper.
Der Artikel Ternärkörper enthält weitere Beispiele für affine Translationsebenen, insbesondere auch ausführlich dargestellte Beispiele für endliche, nichtdesarguesche Translationsebenen (siehe im Unterabschnitt Beispiele der Ordnung 9).
Literatur
- Wendelin Degen, Lothar Profke: Grundlagen der affinen und euklidischen Geometrie. 1. Auflage. Teubner, Stuttgart 1976, ISBN 3-519-02751-8.
- Günter Pickert: Axiomatische Begründung der ebenen euklidischen Geometrie in vektorieller Darstellung. In: Mathematisch-physikalische Semesterberichte. Band 10, 1963, ISSN 0025-5823, S. 65–85.
Anmerkungen
- ↑ Die Translationsgruppe ist genau dann trivial, also die einelementige Gruppe, wenn es außer der identischen Abbildung keine Translation gibt. In diesem Fall ist die Translationsgruppe kommutativ, aber ihr einziger Endomorphismus ist die Identität, der hier definierte Ring der spurtreuen Endomorphismen wäre also ein Nullring.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 03.05. 2021