Fano-Axiom
Das Fano-Axiom ist in der synthetischen
Geometrie ein Inzidenzaxiom sowohl für affine
Ebenen als auch für projektive
Ebenen. Es ist nach dem italienischen Mathematiker Gino Fano benannt. In affinen
oder projektiven Ebenen über einem Schiefkörper
oder Körper
gilt das Fano-Axiom genau dann, wenn die Charakteristik
von
nicht 2 ist. Die ebenfalls nach Fano benannte Fano-Ebene,
das Minimalmodell einer projektiven Ebene, erfüllt das Fano-Axiom
nicht.
Affines Fano-Axiom

Eine affine Ebene
erfüllt das Fano-Axiom, wenn dort gilt (vgl. die Abbildung rechts):
- „Bei jedem nichtausgearteten Parallelogramm schneiden sich die Diagonalen.“ Oder gleichwertig:
- „In keinem nichtausgearteten Parallelogramm sind die Diagonalen parallel.“
Ausführlich und formaler lautet das Axiom so: Sind
Punkte der affinen Ebene
,
von denen keine drei auf einer Geraden liegen, dann gilt: Aus
und
folgt
.
Für eine affine Translationsebene sind die folgenden Aussagen beide äquivalent zum Fano-Axiom:
- Keine Translation hat die Ordnung
2, das heißt für jede Translation
folgt aus
, dass
ist.
- Der Schiefkörper S der spurtreuen Endomorphismen der Translationsgruppe hat eine von 2 verschiedene Charakteristik.
Für eine beliebige affine Ebene folgt die erste dieser Aussagen aus dem Fano-Axiom.
Für jede affine Translationsebene gilt die Alternative:
- Entweder sind in jedem nichtausgearteten Parallelogramm die Diagonalen parallel oder
- in jedem nichtausgearteten Parallelogramm schneiden sich die Diagonalen.
Im ersten Fall hat jede nichtidentische Translation die Ordnung ,
im zweiten Fall haben ebenfalls alle nichtidentischen Translationen dieselbe
Ordnung, diese ist entweder eine ungerade Primzahl
oder unendlich, dann setzt man
.
In all diesen Fällen ist
zugleich die Charakteristik des oben beschriebenen Schiefkörpers S.
Mittelpunkte einer Strecke
In einer affinen Ebene, die dem Fano-Axiom genügt, kann man einer Strecke
Mittelpunkte
zuordnen:
- Falls
ist, setzt man
und nennt
den „Mittelpunkt der Strecke
“.
- Falls
ist, wählt man einen beliebigen Punkt
außerhalb der Gerade
und ergänzt zu einem nichtausgearteten Parallelogramm
. Die Parallele zu
durch den Diagonalenschnittpunkt
schneidet
in einem Punkt
. Alle Punkte
, die so (bei wechselnden Hilfspunkten
) konstruierbar sind, heißen „Mittelpunkte der Strecke
“.
Punktspiegelung
Eine Kollineation
auf einer affinen Fano-Ebene heißt Punktspiegelung, wenn
ein Punkt
existiert, der ein Mittelpunkt für jede Verbindungsstrecke
ist.
- Zu einem beliebigen Punkt
muss im Allgemeinen keine Punktspiegelung an
existieren.
- Im Falle ihrer Existenz ist die Punktspiegelung
an
durch
eindeutig bestimmt. Dann ist für eine beliebige Punkt-Bildpunktstrecke
der Punkt
der einzige Mittelpunkt.
- Jede Punktspiegelung ist eine Dilatation
und also eine Affinität,
denn ihre projektive Fortsetzung ist eine ebene
Perspektivität. Der einzige Fixpunkt der Affinität und das Zentrum der
projektiven Fortsetzung ist der Mittelpunkt
einer beliebigen Punkt-Bildpunktstrecke
.
- Jede Punktspiegelung ist involutorisch.
- In einer affinen Translationsebene und erst recht in einer desarguesschen
Ebene existiert zu jedem Punkt
eine Punktspiegelung an
. Sie ist die zentrische Streckung um
mit dem Streckungsfaktor
.
Projektives Fano-Axiom
Es wurden zwei projektive Formen des Fano-Axioms formuliert, die zueinander dual und äquivalent sind. Dazu werden die Begriffe vollständiges Viereck bzw. vollständiges Vierseit benötigt, die ebenfalls zueinander dual sind.
Vollständiges Viereck
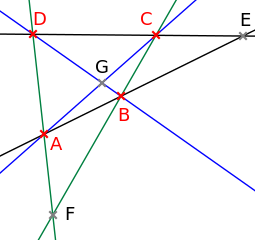
Ein vollständiges Viereck in einer projektiven Ebene besteht aus 4 Punkten (den Ecken des Vierecks) in allgemeiner Lage, das heißt keine drei davon liegen auf einer gemeinsamen Gerade. Die 6 Verbindungsgeraden der Ecken heißen die „Seiten“ des Vierecks, je zwei Seiten, die nicht durch eine gemeinsame Ecke gehen, heißen „Gegenseiten“ des Vierecks.
Ein vollständiges Viereck heißt „Anti-Fano-Viereck“, wenn die Schnittpunkte der Gegenseiten auf einer Geraden liegen, sonst heißt es „Fano-Viereck“.
→ Ein vollständiges Viereck, aufgefasst als geordnete Menge von vier Punkten, bildet eine projektive Punktbasis.
Das projektive Axiom
Das projektive Fano-Axiom lautet:
- „Die Schnittpunkte der Gegenseiten (Diagonalpunkte) in einem beliebigen vollständigen Viereck sind nicht kollinear.“
Das Fano-Axiom fordert also, dass jedes vollständige Viereck der projektiven Ebene ein Fano-Viereck ist. Dann nennt man die projektive Ebene eine Fano-Ebene. Ist dagegen jedes vollständige Viereck ein Anti-Fano-Viereck, dann wird die projektive Ebene gelegentlich als Anti-Fano-Ebene bezeichnet.
Bemerkungen
Zum projektiven Fano-Axiom ist zu beachten:
- Es gibt projektive Ebenen, die weder Fano- noch Anti-Fano-Ebenen sind, siehe weiter unten in diesem Artikel.
- Jede desarguesche projektive Ebene ist entweder eine Fano- oder eine Anti-Fano-Ebene. Sie ist eine Anti-Fano-Ebene, wenn die Charakteristik ihres Koordinatenschiefkörpers 2 ist, und eine Fano-Ebene bei jeder anderen Charakteristik.
- Allgemeiner ist sogar jede Moufangebene entweder
eine Fano- oder eine Anti-Fano-Ebene. Dort lautet das Kriterium: Ist
der Kern
des Koordinatenalternativkörpers
der Ebene, dann ist diese Ebene eine Anti-Fano-Ebene, wenn die Charakteristik dieses Schiefkörpers
ist, und eine Fano-Ebene bei jeder anderen Charakteristik von
.
- Die Fano-Ebene ist im axiomatischen Sinn eine Anti-Fano-Ebene!
Beziehungen des projektiven zum affinen Fano-Axiom
- Durch Ausschneiden einer projektiven Gerade („Schlitzen“) bzw. projektive Erweiterung entsteht aus einer projektiven desargueschen Fano-Ebene stets eine affine desarguesche Ebene, die das affine Fano-Axiom erfüllt, und umgekehrt.
- Durch Schlitzen einer Moufangebene, in der das projektive Fano-Axiom gilt, entsteht stets eine affine Translationsebene, in der das affine Fano-Axiom gilt.
- Falls die projektive Erweiterung einer affinen Translationsebene, die das Fano-Axiom erfüllt, eine Moufangebene ist, dann erfüllt auch diese Moufangebene das Fano-Axiom.
- Durch Schlitzen einer projektiven Fano-Ebene entsteht stets eine affine Ebene, die dem affinen Fano-Axiom genügt.
Vollständiges Vierseit
Ein vollständiges Vierseit in einer projektiven Ebene besteht aus 4 Geraden (den Seiten des Vierseits) in allgemeiner Lage, das heißt keine drei davon gehen durch einen gemeinsamen Punkt. Die 6 Schnittpunkte der Seiten heißen die „Ecken“ des Vierseits, je zwei Ecken, die nicht auf einer Seite liegen, heißen „Gegenecken“ des Vierseits.
Die duale Form des projektiven Fano-Axioms lautet:
- „Die Verbindungsgeraden der Gegenecken (Diagonalen) in einem beliebigen vollständigen Vierseit sind nicht kopunktal.“
Es gilt: Für jede Fano-Ebene ist auch ihre duale Ebene eine Fano-Ebene.
Das ist gleichbedeutend dazu, dass für jede projektive Ebene Fano-Axiom und duales Fano-Axiom äquivalent sind.
Projektive Ebenen mit Fano- und Antifano-Vierecken und der Satz von Desargues
Endliche Ebenen
Der folgende Satz von Gleason
besagt, dass eine endliche Anti-Fano-Ebene (im amerikanischen Sprachgebrauch
leider, etwa hier von Andrew Gleason, oftmals als fano plane bezeichnet…) stets desarguesch und
damit eine
über einem endlichen
Körper
ist:
- Aus der Kollinearität der Diagonalpunkte aller vollständigen Vierecke in einer endlichen projektiven Ebene folgt die Allgemeingültigkeit des Satzes von Desargues in dieser Ebene.
Beispiele für echte, endliche Halbkörper gerader Ordnung, also Quasikörper, die beide Distributivgesetze erfüllen, aber keine Alternativkörper sind, wurden von Donald Ervin Knuth in seiner Dissertation angegeben. Siehe zu dieser Literaturangabe den Artikel Halbkörper (Geometrie). Dort sind im Abschnitt Beispiele zwei solche Halbkörper der Ordnung 16 konkret angegeben.
Die projektiven Ebenen über all diesen „Knuthschen“ echten Halbkörpern
gehören der Lenz-Barlotti-Klasse
V an. Sie können nach dem Satz von Gleason das Anti-Fano-Axiom nicht
erfüllen, da sie nichtdesarguessch sind. Andererseits enthalten sie
die Fanoebene
als Unterstruktur (der Primkörper
mit 2 Elementen ist im Kern des Halbkörpers als Teilkörper enthalten) und damit
auch Anti-Fano-Vierecke.
Umgekehrt vermutet Günter Pickert: In jeder endlichen, nichtdesarguesschen Ebene existieren Fano- und Anti-Fano-Vierecke! Er beweist dazu einen allerdings wesentlich schwächeren Satz von Hanna Neumann:
- Ist p eine Primzahl, r eine positive ganze Zahl, für die
zusätzlich
im Fall
gelten soll, so gibt es eine endliche projektive Ebene der Ordnung
, in der sowohl ein vollständiges Viereck mit kollinearen Diagonalpunkten wie ein solches mit nichtkollinearen Diagonalpunkten vorkommt.
Die von Pickert zum Beweis konstruierten Ebenen sind durch echte Quasikörper der
Ordnung
koordinatisierbar. Das heißt: Sie und die oben erwähnten Ebenen von Knuth
können so geschlitzt werden, dass eine affine Translationsebene der
Ordnung q entsteht. In dieser affinen Ebene gilt dann entweder
- die Diagonalen jedes nichtausgearteten Parallelogramms sind parallel oder
- die Diagonalen jedes nichtausgearteten Parallelogramms schneiden einander.
Der erste Fall tritt genau dann ein, wenn
ist, der zweite, wenn p ungerade ist. Damit zeigt dieser Beweis zugleich,
dass bereits für affine Translationsebenen aus der Gültigkeit des affinen
„Anti-Fano-Axioms“
bzw. des affinen Fano-Axioms im Allgemeinen nicht auf die Gültigkeit des
entsprechenden Axioms im projektiven Abschluss geschlossen werden kann.
Beliebige Ebenen
Pickert ersetzt die Endlichkeitsvoraussetzung des Satzes von Gleason durch
eine Transitivitätsvoraussetzung. Siehe dazu die Definitionen und
Sprachregelungen, die im Artikel Klassifikation
projektiver Ebenen erläutert sind. Er beweist damit: „Gibt es in einer
projektiven Ebene drei nicht kollineare Punkte ,
so dass die Ebene
-
und
-
transitiv ist, und sind in dieser Ebene in jedem vollständigen Viereck die
Diagonalpunkte kollinear, dann ist die Ebene desarguessch.“
Bedeutung
- Die Bedeutung des Fano-Axioms für die elementare affine Geometrie liegt auf der Hand: In beliebigen Ebenen ist die Gültigkeit des Fano-Axioms notwendig, in desarguesschen Ebenen auch hinreichend dafür, dass zu zwei verschiedenen Punkten ein Mittelpunkt existiert! Ohne Fano-Axiom gibt es keine Seitenhalbierenden, keine Mittelsenkrechten, keine Punktspiegelungen usw.
- Etwas weniger offensichtlich ist seine Nützlichkeit bei der Untersuchung von Quadratischen Formen: Hier möchte man gerne durch 2 teilen können (zum Beispiel beim quadratischen Ergänzen und beim "Symmetrisieren" einer Formmatrix, siehe projektive Quadrik).
- Macht man, wie das in der Linearen Algebra gerne getan wird, die generelle Voraussetzung, dass die Charakteristik der betrachteten Koordinatenkörper nicht 2 sei, so geht man auch einigen Sonderfällen aus dem Weg, die nur bei affinen Geometrien mit 2 Punkten auf jeder Geraden (siehe Kollineation) bzw. nur beim Minimalmodell der projektiven Geometrie (siehe Fano-Ebene) auftreten, aber nicht direkt wegen der Charakteristik des Körpers, sondern wegen der Kleinheit der Modelle.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.06. 2021