Klassifikation projektiver Ebenen
Die übliche Klassifikation projektiver Ebenen erfolgt in der synthetischen Geometrie anhand der Operation der jeweiligen Gruppe ihrer Kollineationen. Die Lenz-Barlotti-Klassifikation klassifiziert die Ebenen durch Eigenschaften der Operation bestimmter Untergruppen ihrer Kollineationsgruppe, sie verfeinert dabei die Lenz-Klassifikation. Dazu wird bei beiden Klassifikationen als Merkmal die Reichhaltigkeit der Untergruppen der Kollineationsgruppe betrachtet, die aus zentral-axialen Kollineationen (ebenen, projektiven Perspektivitäten) mit je einer festen Achse und einem festen Zentrum bestehen.
Dabei zeigt sich, dass die gröbere Klasseneinteilung nach Lenz in der Regel jeder Klasse von Ebenen eine für sie charakteristische Klasse von Ternärkörpern zuordnet: Der Koordinatenbereich einer „höheren“ Lenz-Klasse erfüllt – bei geeigneter Wahl der projektiven Punktbasis für die Koordinatisierung – stärkere algebraische Axiome als der einer niedrigeren.
Die Lenz-Barlotti-Klassifikation ist keine Klassifikation „bis auf Isomorphie“: Isomorphe projektive Ebenen gehören stets zur gleichen Klasse, aber Ebenen einer Klasse brauchen nicht zueinander isomorph zu sein. Die einzigen Ausnahmen sind die Lenz-Barlotti-Klassen IVa.3 und IVb.3: In diesen Klassen sind alle Vertreter jeweils zueinander isomorphe Ebenen der Ordnung 9.
Geschichte
Hanfried Lenz entwickelte in den 1940er Jahren eine Klassifikation für projektive Ebenen, die Lenz-Klassifikation. Dabei definierte er als charakteristisches Merkmal die später ebenfalls nach ihm benannte Lenz-Figur einer projektiven Ebene, eine Menge von Paaren, die jeweils von einer Achse (Fixpunktgerade) und einem Punkt (dem Zentrum) auf dieser Achse gebildet werden. Adriano Barlotti erweiterte und verfeinerte diese Klassifikation in den 1950er Jahren dadurch, dass er für die charakteristische Figur auch Zentren außerhalb der Achse zuließ. Damit wird aus der Lenz-Figur die Lenz-Barlotti-Figur.
Günter Pickert entwickelte in den 1960er Jahren eine formale Definition des klassischen Begriffes Schließungssatz mit dem sich auch „Spezialisierungen“ eines Schließungssatzes und affine Formen (Spezialisierungen mit einer ausgezeichneten, konstanten Geraden, der Ferngeraden) fassen und vergleichen lassen. Der für die Klassifikation projektiver Ebenen wichtige Schließungssatz ist der Satz von Desargues, alle „Transitivitätseigenschaften“, die eine Lenz- oder Lenz-Barlotti-Klasse charakterisieren, sind der Gültigkeit einer Spezialisierung des desarguesschen Satzes zusammen mit der Nichtgültigkeit einer anderen seiner Spezialisierungen gleichwertig. Pickert konnte auch zeigen, dass die Gültigkeit jedes Schließungssatzes äquivalent zur Gültigkeit bestimmter algebraischer Axiome in einem geeignet gewählten Koordinatenternärkörper ist. Die Lenz-Barlotti-Klassifikation liefert insofern zugleich eine Klassifikation der Koordinatenternärkörper. Während aber die Klassen der algebraischen Axiome und der Schließungssätze prinzipiell unbeschränkt sind, liefert die Lenz-Barlotti-Klassifikation anhand der Automorphismengruppe der Ebene eine endliche Anzahl von Klassen.
Definitionen
Im Folgenden sei
eine projektive
Ebene und zugleich die Menge der auf der Ebene liegenden projektiven Punkte
und
die Menge der Geraden der Ebene,
die Gruppe der Kollineationen
der Ebene. Eine Kollineation
heißt
-Kollineation,
wenn sie die Achse
und das Zentrum
hat, das heißt, wenn gilt:
- Für jeden Punkt
ist
und
- Für jede Gerade
, die durch
geht, ist
.
Mit
wird die Untergruppe der
-Kollineationen
der Ebene bezeichnet. Die projektive Ebene heißt
-transitiv,
wenn die Gruppe
für jede Gerade
mit
transitiv
auf
operiert.
Figuren
Die Menge
heißt Lenz-Figur von .
Die Menge
heißt Lenz-Barlotti-Figur von .
Invarianz der Figuren
Sowohl die Lenz-Figur, als auch die Lenz-Barlotti-Figur sind invariant unter jeder Kollineation, das heißt konkret:
Ist
eine projektive Ebene und
eine beliebige Kollineation dieser Ebene, dann gilt
und
.
Koordinatisierung der projektiven Ebene
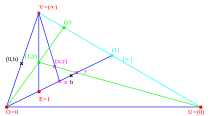
Für Ebenen der Lenz-Klassen I bis IV ist die algebraische Struktur der Koordinatenternärkörper von der Wahl des projektiven Koordinatensystems abhängig und von der darauf beruhenden Definition der Ternärkonstruktion. Die im nächsten Abschnitt beschriebenen Lenz-Barlotti-Figuren werden mit Hilfe des hier beschriebenen Koordinatenbezugssystems angegeben. Dazu wird eine Koordinatendarstellung der Punkte mit abgekürzten Koordinaten auf der Ferngeraden eingeführt, vergleiche dazu die Abbildung rechts, die Koordinatisierung und die Bezeichnungen richten sich nach Prieß-Crampe, sie gehen auf Marshall Hall zurück:
- Ein projektives Koordinatensystem wird durch geeignete Wahl eines
vollständigen
Vierecks
auf der Lenz-Barlotti-Figur bestimmt.
- Der Punkt O wird zum Ursprung des affinen Koordinatensystems,
ist die Ferngerade, die affinen Punkte auf
, also die Punkte in
bilden den Ternärkörper.
- Der Punkt O wird zum neutralen Element der Addition und als Element von K mit 0 bezeichnet.
- Der Punkt E wird zum neutralen Element der Multiplikation und als Element von K mit 1 bezeichnet.
- Alle Elemente der affinen Gerade K haben als affine Koordinaten
- Der Punkt mit den Koordinaten
ist bestimmt als Schnittpunkt der Geraden
und
. Umgekehrt erhält man die Koordinaten eines affinen Punktes
als Schnittpunkte
und
.
- Spezialfälle:
- Die affinen Punkte B auf der Geraden
, also alle Punkte dieser Geraden außer V, haben die Koordinaten
, wobei das Ternärkörperelement (Koordinate)
als Schnittpunkt
bestimmt ist. Dieser Spezialfall der Koordinatenkonstruktion ist in der Abbildung schwarz dargestellt.
- Die affinen Punkte Y auf der Geraden
, also alle Punkte dieser Geraden außer V, haben die Koordinaten
, wobei die Koordinate
als Schnittpunkt
bestimmt ist. Dieser Spezialfall der Koordinatenkonstruktion ist in der Abbildung grün dargestellt.
- Ein Punkt
auf der Ferngeraden erhält die Koordinatendarstellung
wobei
dadurch bestimmt ist, dass der Schnittpunkt
die affinen Koordinaten
hat. Der Punkt V, dem auf diese Art keine Koordinate zugewiesen werden kann, erhält die Koordinatendarstellung
.
- Die affinen Punkte B auf der Geraden
Ternärverknüpfung und Geradendarstellung
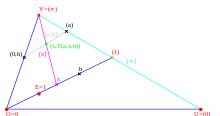
Die Ternärverknüpfung
wird nun für
so definiert, vergleiche die zweite Abbildung rechts:
- Zu
wird der Fernpunkt
konstruiert.
- Zu
wird der Punkt
konstruiert.
- Das Ergebnis
ist bestimmt als die y-Koordinate des Schnitts
, der in der Abbildung grün dargestellt ist.
Diese Ternärverknüpfung ist der im Artikel Ternärkörper beschriebenen affinen Definition äquivalent. Anders als dort beschrieben, werden hier die Geraden durch in der zweiten Koordinate y explizite Gleichungen (und zwei Sonderformen) dargestellt:
- Die Geraden
haben die explizite Geradengleichung
für die affinen Punkte und den Fernpunkt
, als Beispiel in der Abbildung die grau dargestellte Verbindungsgerade
. Dies sind alle Geraden der projektiven Ebene, außer denen durch
. Ein Spezialfall sind die Verbindungsgeraden
mit der affinen Gleichung
und dem Fernpunkt
.
- Die Geraden
durch V, die
in einem affinen Punkt
schneiden, haben die Gleichung
für die affinen Punkte und den Fernpunkt
. Ein Beispiel ist die Gerade
in der Abbildung.
- Die Ferngerade
enthält genau die Punkte mit den Koordinaten
.
Im affinen Ausschnitt der Ebene sind Geraden genau dann parallel, wenn ihre
projektive Fortsetzungen durch denselben Fernpunkt
gehen, daher gilt für die Parallelenscharen:
- Zwei Geraden
sind genau dann parallel, wenn
ist. Diese Zahl ist die gemeinsame Steigung der zugehörigen Parallelenschar.
- Alle Geraden vom zweiten Typ
sind zueinander, aber zu keiner Geraden des ersten Typs parallel.
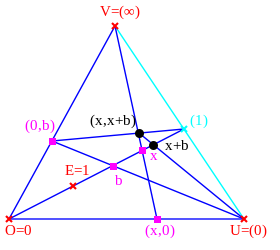
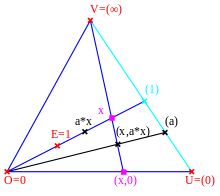
Konstruktion der zweistelligen Verknüpfungen
Auf jeder projektiven Ebene werden durch die Wahl eines
Koordinatenbezugssystem
auch zwei zweistellige Verknüpfungen, eine Addition
und eine Multiplikation
auf der affinen Punktmenge
festgelegt. Die oben beschriebene Ternärverknüpfung ist auf allen Ebenen außer
denen der Lenz-Barlotti-Klasse I.1, also auf allen Ebenen über einem
linearen Ternärkörper durch diese zweistelligen Verknüpfungen als
darstellbar.
In den Abbildungen unten sind diese Spezialfälle der Ternärverknüpfung dargestellt.
 |
|
| Addition |
Multiplikation |
Die Klassen und ihre Eigenschaften
Lenz-Klassen
Lenz ordnet jeder Lenz-Figur eine Ordnungszahl in Form einer römischen Zahl zwischen I und VII zu. Eine Klasse mit einer höheren Klassenzahl erfüllt alle Eigenschaften der Klassen mit niedrigeren Zahlen, aber ihre Lenz-Figur ist eine echte Obermenge von Lenzfiguren der niedrigeren Klassen. Die Klassenzahl VI entfällt, da gezeigt wurde, dass keine projektive Ebene mit der entsprechenden Lenz-Figur existiert. Stattdessen hat bereits Lenz die Klasse IV in zwei Unterklassen IVa und IVb aufgeteilt, die dual zueinander sind.
Eine projektive Ebene
hat genau eine der im Folgenden genannten Lenz-Figuren:
| Lenz-Typ | Lenz-Figur | Koordinatenbereich |
|---|---|---|
| I | Ternärkörper | |
| II | Es gibt eine Achse |
kartesische Gruppe |
| III | Es gibt eine Gerade
|
spezielle kartesische Gruppe (stets unendlich!) |
| IVa | Es gibt eine Achse |
Linksquasikörper |
| IVb | Es gibt ein Zentrum |
Rechtsquasikörper[1] |
| V | Es gibt eine Achse
|
Halbkörper |
| VII | Alternativkörper |
Ebenen, die mindestens den Lenz-Typ IVa haben, also zu einer der Klassen IVa, V oder VII gehören, werden auch als projektive Translationsebenen bezeichnet. Schlitzt man eine solche Ebene längs einer Achse, die zur Lenzfigur gehört, dann entsteht eine affine Translationsebene. Bei Ebenen der Lenz-Klassen IVb, V oder VII ist die duale Ebene eine projektive Translationsebene in diesem Sinn. Nur bei Ebenen der Lenz-Klasse VII ist die algebraische Struktur des Koordinatenbereichs unabhängig von der Wahl des projektiven Koordinatensystems, hier sind alle Koordinatenbereiche zueinander isomorphe Alternativkörper, siehe dazu Moufangebene. Für eine Ebene der Klasse V sind die Koordinatenbereiche zueinander isotope Halbkörper. Bei den Klassen I bis IV sind die Koordinatenkörper zueinander isotope Ternärkörper und nur bei geeigneter Wahl des Koordinatensystems haben sie die in der Tabelle genannte „stärkst-mögliche“ algebraische Struktur.
Lenz-Barlotti-Klassen
Die Lenz-Barlotti-Klassifikation
verfeinert die Lenz-Klassifikation, indem bei der Lenz-Barlotti-Figur auch
zugelassen wird, dass das Zentrum nicht auf der Achse liegt. Die römischen
Zahlen nach Lenz werden beibehalten, ihnen werden, durch einen Punkt getrennt,
arabische Ziffern angefügt. Jede Lenz-Barlotti-Klasse ist eine Unterklasse der
oben beschriebenen Lenz-Klassifikation. Damit zerfiel zum Beispiel die Klasse I
von Lenz bei Barlotti ursprünglich in 8 Unterklassen (I.1 bis I.8), wobei sich
später zeigte, dass keine Vertreter der Klassen I.5, I.7 und I.8 existieren. Die
Lenz-Klasse V zerfällt als Einzige in der Lenz-Barlotti-Klassifikation nicht
weiter, hier gilt .
Ansonsten stimmt die Lenz-Barlotti-Figur für die jeweils erste
Lenz-Barlotti-Klasse mit der Lenz-Figur der entsprechenden übergeordneten
Lenz-Klasse überein.
Eine projektive Ebene
hat genau eine der im Folgenden genannten Lenz-Barlotti-Figuren:
| Lenz-Barlotti-Typ | Lenz-Barlotti-Figur | Ternärkörper K bezüglich |
|---|---|---|
| I.1 | keine zusätzlichen Eigenschaften | |
| I.2 | K ist linear, Multiplikation ist assoziativ | |
| I.3 | K ist linear, Multiplikation ist assoziativ, | |
| I.4 | K ist linear, Multiplikation ist assoziativ, beide Distributivgesetze | |
| I.6 | K ist linear, Multiplikation ist assoziativ, beide Distributivgesetze, weitere spezielle Eigenschaften | |
| II.1 | Kartesische Gruppe | |
| II.2 | Kartesische Gruppe, assoziative Multiplikation | |
| III.1 | Kartesische Gruppe mit speziellen Eigenschaften | |
| III.2 | Kartesische Gruppe mit speziellen Eigenschaften, assoziative Multiplikation | |
| IVa.1 | Linksquasikörper: | |
| IVa.2 | (Links-)Fastkörper | |
| IVa.3 | eindeutig bestimmter Linksfastkörper mit 9 Elementen. | |
| IVb.1 | Die Lenz-Barlotti-Figur ist dual zu der von Klasse IVa.1. | Dual zu IVa.1. |
| IVb.2 | Die Lenz-Barlotti-Figur ist dual zu der von Klasse IVa.2. | Dual zu IVa.2. |
| IVb.3 | Die Lenz-Barlotti-Figur ist dual zu der von Klasse IVa.3. | Dual zu IVa.3. |
| V | Halbkörper | |
| VII.1 | Alternativkörper | |
| VII.2 | Schiefkörper |
Modelle
In diesem Abschnitt findet sich eine Übersicht über heute bekannte Beispiele (Stand: 2011) für Ebenen, die Vertreter bestimmter Lenz-Barlotti-Klassen sind. Insbesondere über unendliche Ebenen, die in die Lenz-Klasse I fallen, ist recht wenig bekannt, endliche Modelle für diese „schwächsten“ Lenz-Barlotti-Klassen werden heute mit massivem Computereinsatz gesucht oder es wird auf diesem Wege versucht, deren Existenz zu widerlegen. Die folgende tabellarische Liste erhebt keinen Anspruch auf Vollständigkeit!
| Lenz-Klasse | Lenz-Barlotti-Klasse | endliche Modelle | unendliche Modelle |
|---|---|---|---|
| I | I.1 | „Hughes planes“:
Zu ungeraden Primzahlen |
Hilbertsche und Beltramische Liniensysteme |
| I.2 | unbekannt.[2] | Ein archimedisch
angeordneter, linearer Ternärkörper | |
| I.3 | Auf einem angeordneten, echten Fastkörper wird analog zur Konstruktion einer reellen Moultonebene mit einer Knickkonstante aus dem Zentrum des Fastkörpers eine Moulton-Ebenenmultiplikation eingeführt. Dann koordinatisiert der entstehende Ternärkörper eine ebene I.3-Ebene. | ||
| I.4 | Ein archimedisch angeordneter, linearer Ternärkörper | ||
| I.6 | Existieren nicht! | unbekannt[2][3] | |
| II | II.1 | Walker-Planes, dies sind Ebenen der Ordnung |
Für beide Lenz-Barlotti-Klassen II.1 und II.2 existieren unendliche Modelle, die sogar eine Anordnung zulassen. Siehe dazu die Beispiele im Artikel Kartesische Gruppe. |
| II.2 | Einige Beispiele der Ordnung | ||
| III | III.1 | Existieren nicht! | Analog zu III.2, aber die Moulton-Ebenen-Multiplikation
wird auf einem angeordneten, nicht kommutativen (damit zwangsläufig
unendlichen) Schiefkörper |
| III.2 | Existieren nicht! | Moulton-Ebenen vom reellen Typ aus einem (unendlichen) angeordneten Körper. | |
| IVa | IVa.1 | Ebenen über endlichen Quasikörpern, die weder Fast- noch Halbkörper
sind. Solche Quasikörper sind zum Beispiel die in Quasikörper#Quasikörper
endlicher Moulton-Ebenen beschriebenen, aus endlichen Körpern
ungerader Primzahlpotenzordnung |
Unendliche Andrésche Quasikörper. Es existiert kein Modell, das eine archimedische Anordnung zulässt. |
| IVa.2 | Ebenen über endlichen Fastkörpern, die keine Halbkörper sind. Solche
Fastkörper sind zum Beispiel die in Quasikörper#Quasikörper
endlicher Moulton-Ebenen beschriebenen, aus endlichen Körpern
ungerader Primzahlpotenzordnung |
Unendliche Andrésche Fastkörper. Es existiert kein Modell, das eine archimedische Anordnung zulässt. | |
| IVa.3 | Es existiert bis auf Isomorphie genau ein Modell: Die projektive, nichtdesarguesche Translationsebene der Ordnung 9 | Existieren nicht! | |
| IVb | IVb.1 | Dual zu IVa.1 | Dual zu IVa.1 |
| VIb.2 | Dual zu IVa.2 | Dual zu IVa.2 | |
| IVb.3 | Es existiert bis auf Isomorphie genau ein Modell: Die duale Ebene zu der Ebene vom Typ IVa.3 | Existieren nicht! | |
| V | V | Unendlich viele Modelle: Für jede Primzahlpotenz |
Unendlich viele Modelle über „echten“ unendlichen Halbkörpern. Beispiele für solche Halbkörper, die sogar eine Anordnung zulassen, lassen sich aus verallgemeinerten formalen Potenzreihen gewinnen. Keine Klasse-V Ebene lässt eine archimedische Anordnung zu. |
| VII | VII.1 | Existieren nicht! (→ Siehe Moufangebene!) | |
| VII.2 | Zu jeder Primzahlpotenzordnung (außer |
Zu jedem unendlichen Schiefkörper |
Anmerkungen
- ↑
Wenn man bei einer Ebene der Lenz-Klasse IVb von
der dualen Ebene ausgeht, also bei der Konstruktion des Koordinatenbereichs
anstelle der Punktmenge
zunächst die Geradenmenge
und ein geeignetes vollständiges Vierseit zugrunde legt, dann kann man dieses Vierseit so wählen, dass der Koordinatenbereich der erneut dualisierten Ebene ein Rechtsquasikörper ist.
- ↑ a b Bis zum Jahr 1975 waren keine Modelle bekannt. Pickert (1975), Anhang, 6: Die Lenz-Barlotti-Klassifizierung
- ↑ Als André am 23. Januar 1964 seinen Artikel schrieb, war die Existenz dieser Klasse ungeklärt! Siehe dort S. 316


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.05. 2021