Satz vom Fußball

Der Satz vom Fußball ist ein mathematischer Satz
aus der linearen
Algebra und Geometrie,
der auf anschauliche Weise die Eigenschaften der Drehgruppe
illustriert. Der Satz gibt die Existenz zweier Fixpunkte auf
einer Kugeloberfläche
an, nachdem die Kugel beliebig oft am Platz gedreht
worden ist. Die mathematische Grundaussage des Satzes wurde mit Hilfe
elementarer geometrischer Argumente erstmals im Jahr 1776 von dem Schweizer
Mathematiker Leonhard
Euler bewiesen.
Aussage
Der Satz vom Fußball lautet wie folgt:
„Bei jedem Fußballspiel gibt es zwei Punkte auf der Oberfläche des Balls, die sich zu Beginn der ersten und der zweiten Halbzeit, wenn der Ball genau auf dem Anstoßpunkt liegt, an derselben Stelle im umgebenden Raum befinden.“
Beweis
Beweisidee
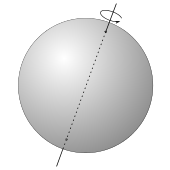
Im Folgenden wird der Fußball idealisiert als Kugel dargestellt. Im Verlauf der ersten Halbzeit führt ein Fußball eine Reihe von Bewegungen im Raum durch. Da der Fußball zu Beginn der zweiten Halbzeit wieder zurück auf den Anstoßpunkt gelegt wird, können im Weiteren die Verschiebungen des Balls außer Betracht bleiben und es brauchen nur die Drehungen des Balls betrachtet zu werden. Jede dieser Drehungen kann durch eine Drehachse und einen Drehwinkel beschrieben werden. Punkte im Raum, die sich auf der Drehachse befinden, verändern bei einer Drehung ihre Position nicht.
Eine wichtige Eigenschaft des dreidimensionalen Raums ist nun, dass jede Hintereinanderausführung von zwei oder mehreren Drehungen durch eine einzige Drehung beschrieben werden kann. Die Drehachse dieser Drehung durchstößt dabei die Oberfläche des Fußballs an zwei diametral gegenüberliegenden Punkten (Antipoden). Diese beiden Punkte müssen sich demnach zu Beginn der ersten und der zweiten Halbzeit an derselben Stelle im Raum befinden.
Beweis
Nach Wahl eines kartesischen
Koordinatensystems mit dem Kugelmittelpunkt als Koordinatenursprung
kann jede Drehung im Raum durch eine Drehmatrix
beschrieben werden. Eine Drehmatrix ist dabei eine orthogonale Matrix
mit Determinante
.
Führt eine Kugel insgesamt
Drehungen durch, dann können diese durch
Drehmatrizen
angegeben werden. Die Hintereinanderausführung dieser Drehungen entspricht dann
dem Matrizenprodukt
der Drehmatrizen. Weil das Produkt zweier orthogonaler Matrizen wieder
orthogonal ist (siehe orthogonale
Gruppe) und die Determinante des Produkts zweier Matrizen gleich dem Produkt
der Determinanten ist (Determinantenproduktsatz),
ist auch die Matrix
wieder eine orthogonale Matrix mit Determinante
.
Sind nun
und
die drei (im Allgemeinen komplexen)
Eigenwerte
von
,
dann gilt
.
Da für die Eigenwerte
einer orthogonalen Matrix
gilt und komplexe Eigenwerte paarweise komplex konjugiert
auftreten, muss mindestens ein Eigenwert von
reell und gleich
sein. Dies bedeutet wiederum, dass es einen Eigenvektor
geben muss, für den
gilt. Ein solcher Vektor
und jedes skalare
Vielfache dieses Vektors wird demnach durch die Matrix
auf sich selbst abgebildet. Die lineare
Hülle
dieses Vektors definiert eine Ursprungsgerade,
die die Kugeloberfläche in zwei Punkten schneidet. Dies sind die beiden
gesuchten Punkte, die bei der Gesamtdrehung festgehalten werden.
Verwendung
Der Satz vom Fußball wird in der neueren mathematischen Literatur häufig als Korollar, das heißt als unmittelbare Folgerung aus vorher bewiesenen Sätzen, angegeben. In einem solchen Fall erweist sich der Beweis des Satzes meist als recht einfach. Gerd Fischer schreibt etwa in seinem Lehrbuch zur linearen Algebra, dass der Satz vom Fußball leichter zu beweisen als anschaulich zu verstehen sei, und beweist ihn dann in einer Zeile.
Der Satz vom Fußball ist ein Spezialfall einer allgemeineren Aussage, nach
der in einem endlichdimensionalen reellen Skalarproduktraum die
orthogonalen
Endomorphismen mit positiver Determinante eine Gruppe, die
sogenannte spezielle
orthogonale Gruppe ,
bilden. Ist die Dimension
des zugrunde liegenden Vektorraums
ungerade, dann hat jede Abbildung in dieser Gruppe den Eigenwert
.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 04.09. 2019