Polytrope Zustandsänderung
In der Thermodynamik
wird eine Zustandsänderung
eines Systems, in der für Druck
und spezifischem
Volumen
die Gleichung
gilt, als polytrop bezeichnet. Der Exponent
wird Polytropenexponent genannt. Bei technischen Vorgängen kann der
Polytropenexponent als konstant angesehen werden.
Eine Polytrope nimmt im p-v-Diagramm
die Form einer Potenzfunktion
mit negativer Steigung an.
Sonderfälle der polytropen Zustandsänderung sind:
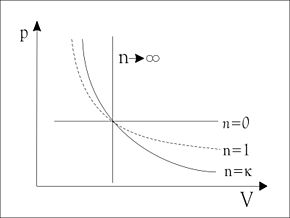
Die einem Gas während dieser Zustandsänderung zugeführte Wärme ist gegeben durch:
Dabei bezeichnet
die Masse,
und
Anfangs- und Endtemperatur des Prozesses. Die Polytropie zeichnet sich durch
eine feste Wärmekapazität
aus, welche sich aus
,
und
ergibt.
Man spricht auch von polytroper Zustandsgleichung:
mit dem Druck p, der Dichte ,
der Polytropenkonstante K und dem Polytropenindex m in
.
Sie findet zum Beispiel Anwendung in der Astrophysik (Lane-Emden-Gleichung).
Ideale Gase
Für ideale Gase, bei isentropen Zustandsänderungen, gelten außerdem folgende Beziehungen:
bzw.
mit
: absolute Temperatur
: Druck
: Volumen.
Bei der isentropen Zustandsänderung eines idealen Gases gilt .
Mit der isobaren Wärmekapazität
und der isochoren Wärmekapazität
.
Bei zweiatomigen Gasen kann
(beispielsweise Luft als Gasgemisch)
und bei einatomigen Gasen (Edelgasen)
angesetzt werden.
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 12.08. 2020