Martingal

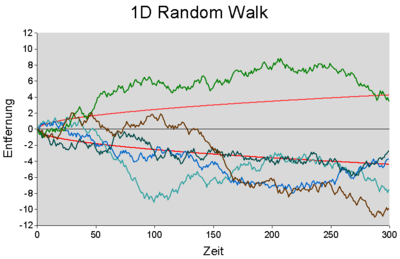
Beim eindimensionalen Random Walk geht man in jedem Schritt (x-Achse) mit Wahrscheinlichkeit 1/2 nach oben oder unten (y-Achse), fünf mögliche Pfade sind dargestellt. Ist $M_{n}$ die Position auf der y-Achse zum Zeitpunkt n, so erhält man ein Martingal $(M_{n})_{n}$ .

Als Martingal bezeichnet man in der Wahrscheinlichkeitstheorie einen stochastischen Prozess, der über den bedingten Erwartungswert definiert wird und sich dadurch auszeichnet, dass er im Mittel fair ist. Martingale entstehen auf natürliche Weise aus der Modellierung von fairen Glücksspielen. Sie wurden von Paul Lévy in die Mathematik eingeführt.

Eng verwandt mit den Martingalen sind die Supermartingale, dies sind stochastische Prozesse, bei denen im Mittel ein Verlust auftritt, und Submartingale, dies sind stochastische Prozesse, bei denen im Mittel ein Gewinn auftritt.

Definition

Diskreter Fall

Gegeben seien ein Wahrscheinlichkeitsraum $(\Omega ,{\mathcal A},P)$ sowie eine Filtrierung $\mathbb {F} =({\mathcal {F}}_{n})_{n\in \mathbb {N} }$ . Gegeben sei ein stochastischer Prozess $X=(X_{n})_{n\in \mathbb {N} }$ auf $(\Omega ,{\mathcal A})$ , für den gilt:

Der Prozess ist ein integrierbarer Prozess, das heißt, es ist $\operatorname {E} (|X_{n}|)<\infty$ für alle $n \in \N$ .
Der Prozess ist adaptiert an $\mathbb F$ , das heißt, $X_{n}$ ist ${\mathcal F}_{n}$ -messbar für alle $n\in \mathbb {N}$ .

Dann heißt ein Martingal (bezüglich $\mathbb F$ ), wenn

$\operatorname {E} (X_{n+1}|{\mathcal {F}}_{n})=X_{n}\quad P\mathrm {-fast\ sicher\ f{\ddot {u}}r\ alle\ } n\in \mathbb {N}$

gilt.

Dabei bezeichnet $\operatorname {E} (Y|{\mathcal {B}})$ den bedingten Erwartungswert der Zufallsvariablen , gegeben die σ-Algebra ${\mathcal B}$ .

Allgemeiner Fall

Sind ein Wahrscheinlichkeitsraum $(\Omega ,{\mathcal A},P)$ sowie eine beliebige, geordnete Indexmenge (meist $T\subset \mathbb {R}$ ) und eine Filtrierung $\mathbb {F} =({\mathcal {F}}_{t})_{t\in T}$ gegeben, so heißt ein integrierbarer, an $\mathbb F$ adaptierter Prozess $X=(X_t)_{t \in T}$ ein Martingal (bezüglich $\mathbb F$ ), wenn für alle $t\in T$ gilt

$\operatorname {E} (X_{s}|{\mathcal {F}}_{t})=X_{t}\quad P\mathrm {-fast\ sicher\ f{\ddot {u}}r\ alle\ } s>t$ .

Supermartingale und Submartingale

Ein integrierbarer und an $\mathbb{F}$ adaptierter diskreter stochastischer Prozess heißt Submartingal, wenn

$\operatorname {E} (X_{n+1}|{\mathcal {F}}_{n})\geq X_{n}\quad P\mathrm {-fast\ sicher\ f{\ddot {u}}r\ alle\ } n\in \mathbb {N}$ ,

und Supermartingal, wenn

$\operatorname {E} (X_{n+1}|{\mathcal {F}}_{n})\leq X_{n}\quad P\mathrm {-fast\ sicher\ f{\ddot {u}}r\ alle\ } n\in \mathbb {N}$

gilt. Im stetigen Falle definiert man analog ein Submartingal über

$\operatorname {E} (X_{s}|{\mathcal {F}}_{t})\geq X_{t}\quad P\mathrm {-fast\ sicher\ f{\ddot {u}}r\ alle\ } s>t$ .

und ein Supermartingal über

$\operatorname {E} (X_{s}|{\mathcal {F}}_{t})\leq X_{t}\quad P\mathrm {-fast\ sicher\ f{\ddot {u}}r\ alle\ } s>t$ .

Submartingale sind also im Gegensatz zu Martingalen tendenziell steigend, Supermartingale tendenziell fallend.

Bemerkung

Die Eigenschaft, ein (Sub-/Super-)Martingal zu sein, kommt nicht stochastischen Prozessen allein zu, sondern immer einem stochastischen Prozess in Kombination mit einer Filtrierung. Daher sollte die Filtrierung immer mit angegeben werden. Manche Autoren geben keine Filtrierung mit an, wenn sie die von dem Prozess selbst erzeugte Filtrierung verwenden, die durch ${\mathcal {F}}_{t}^{E}:=\sigma ({X_{s};s\leq t})$ gegeben ist. Wenn $(X_{t})_{{t\in T}}$ ein Martingal bezüglich einer Filtrierung $({\mathcal {F}}_{t})_{t\in T}$ ist, dann ist es auch ein Martingal bezüglich $({\mathcal {F}}_{t}^{E})_{t\in T}$ .

Motivierendes Beispiel

Der Begriff des Martingals lässt sich als Formalisierung und Verallgemeinerung eines fairen Glücksspiels auffassen. Sei dazu M_0 das Startkapital des Spielers. Dieses wird in vielen Fällen eine Konstante sein, aber auch ein zufälliges Startkapital ist denkbar. Der zufällige Gewinn im ersten Spiel werde mit $X_{1}$ bezeichnet. Er kann positiv, null oder negativ (also ein Verlust) sein. Das Kapital des Spielers nach dem ersten Spiel beträgt $M_{1}=M_{0}+X_{1}$ und allgemein nach dem -ten Spiel

$M_{n}=M_{0}+\sum _{{k=1}}^{n}X_{k},$

wenn $X_{k}$ den Gewinn im -ten Spiel bezeichnet. Bei einem fairen Glücksspiel ist der Erwartungswert jedes Gewinns gleich null, d.h., es gilt $E(X_{k})=0$ für alle $k\in\N$ .

Der Spielverlauf werde nun bis zum Zeitpunkt einschließlich beobachtet, d.h. die Kapitalstände $M_{0},M_{1},\dots ,M_{n}$ seien bekannt. Falls nun der Gewinn im nächsten, also im n+1 -ten, Spiel unabhängig vom bisherigen Spielverlauf ist, dann berechnet sich das erwartete Gesamtkapital $M_{{n+1}}=M_{n}+X_{{n+1}}$ nach dem nächsten Spiel unter Berücksichtigung aller zur Verfügung stehenden Informationen mit Hilfe der Rechenregeln für bedingte Erwartungswerte als

$E(M_{n+1}\mid M_{0},\dots ,M_{n})=E(M_{n}\mid M_{0},\dots ,M_{n})+E(X_{n+1}\mid M_{0},\ldots ,M_{n})=M_{n}+E(X_{n+1})=M_{n}.$

Damit ist gezeigt, dass sich das Kapital eines Spielers, der an einem fairen Glücksspiel teilnimmt, als Martingal modellieren lässt.

Bei realen Glücksspielen, wie beispielsweise beim Roulette, ist jedoch wegen des Bankvorteils der erwartete Gewinn bei jedem Spiel im Allgemeinen negativ, also $E(X_{k})<0$ . Dann ergibt sich analog zur obigen Rechnung

$E(M_{{n+1}}\mid M_{0},\dots ,M_{n})\leq M_{n}.$

Aus Sicht des Spielers handelt es sich in diesem Fall um ein Supermartingal (Merkspruch: „Supermartingale sind super für die Spielbank“).

Beispiele

Von einer Filtrierung erzeugtes Martingal

Ist $(\Omega ,{\mathcal A},P)$ ein Wahrscheinlichkeitsraum, $\mathbb {F} =({\mathcal {F}}_{n})_{n\in \mathbb {N} }$ eine Filtration und eine -integrierbare Zufallsvariable auf $(\Omega ,{\mathcal A})$ . Dann wird durch

$X_{n}:=\operatorname {E} (X|{\mathcal {F}}_{n})$

ein Martingal (bezüglich $\mathbb F$ ) definiert.

Um zu zeigen, dass es sich um ein Martingal handelt, rechnet man die Definition nach:

$\operatorname {E} (X_{n+1}|{\mathcal {F}}_{n})=\operatorname {E} (\operatorname {E} (X|{\mathcal {F}}_{n+1})|{\mathcal {F}}_{n})=\operatorname {E} (X|{\mathcal {F}}_{n})=X_{n}$ .

Somit handelt es sich um ein Martingal. Dabei ist die erste Umformung das Einsetzen der Definition, die zweite eine Anwendung der Turmregel des bedingten Erwartungswertes und die dritte wieder Einsetzen der Definition.

Doob-Martingal

Ein Spezialfall des obigen Martingals sind Doob-Martingale: Ist eine P-integrierbare Zufallsvariable gegeben und wird die Filtrierung durch eine Folge von Zufallsvariablen $(Y_{n})_{n\in \mathbb {N} }$ erzeugt, also

${\mathcal {F}}_{n}:=\sigma (Y_{0},\dots ,Y_{n})$ ,

so heißt das Martingal, welches durch

$X_{n}:=\operatorname {E} (X|{\mathcal {F}}_{n})=\operatorname {E} (X|Y_{0},\dots ,Y_{n})$

definiert wird, ein Doob-Martingal (benannt nach Joseph L. Doob).

Beispiele für zeitstetige Martingale

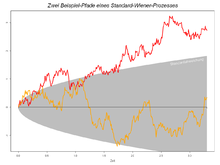
Wiener-Prozess als Beispiel für ein Martingal

Ein Wiener-Prozess ist ein Martingal, ebenso sind für einen Wiener-Prozess die Prozesse $W_{t}^{2}-t$ und die geometrische brownsche Bewegung ohne Drift $a\exp \left(\sigma W_{t}-{\frac {\sigma ^{2}}{2}}t\right)$ Martingale.
Ein Poisson-Prozess mit Rate $\lambda$ , der um seine Drift bereinigt wird, also ${\hat P}_{{\lambda ,t}}=P_{{\lambda ,t}}-\lambda t$ , ist ein Martingal.
Nach dem Lemma von Itō gilt: Jedes Itō-Integral (mit beschränktem Integranden) ist ein Martingal. Nach dem Itoschen Martingaldarstellungssatz lässt sich umgekehrt jedes Martingal (sogar jedes lokale Martingal) bezüglich einer von einer Brownschen Bewegung erzeugten Filtration als Ito-Integral bezüglich ebendieser Brown'schen Bewegung darstellen.
Jedes stetige Martingal ist entweder von unendlicher Variation oder konstant.
Jedes gestoppte Martingal ist wieder ein Martingal.

Gestoppte Brownsche Bewegung als Beispiel für ein Martingal

Eigenschaften

Rechenregeln

ist genau dann ein Submartingal, wenn ein Supermartingal ist
Sind (Sub-)Supermartingale und ist $a,b\geq 0$ , dann ist auch ein (Sub-)Supermartingal.
Sind Martingale, so ist auch ein Martingal für $a,b \in \R$ .
Sind Supermartingale, dann ist auch

$Z= (\min(X_t,Y_t))_{t \in T}$

ein Supermartingal.

Sind Submartingale, dann ist auch

$Z= (\max(X_t,Y_t))_{t \in T}$

ein Submartingal.

Ist $\varphi$ eine konvexe Funktion und ein Martingal und gilt $\operatorname E (\varphi(X_t)^+) < \infty$ , so ist $(\varphi(X_t))_{t \in T}$ ein Submartingal.

Einfluss der Filtrierung

Sind zwei Filtrierungen $\mathcal F, \mathcal F^*$ gegeben und ist ${\mathcal {F}}$ kleiner als $\mathcal F^*$ in dem Sinne, dass für jedes gilt $\mathcal F_t \subset \mathcal F^*_t$ , so ist jedes $\mathcal F^*$ -Martingal auch ein ${\mathcal {F}}$ -Martingal.

Quadratische Variation und Exponentialmartingal

Ist die quadratische Variation $\langle M\rangle$ eines stetigen beschränkten Martingals M_t (oder eines mit endlichen exponentiellen Momenten) endlich, so ist der stochastische Prozess

$X_{t}=M_{t}^{2}-\langle M\rangle _{t}$

ebenfalls ein Martingal.

Ebenso ist das sogenannte Exponentialmartingal von M_t , gegeben durch

> $X_{t}=e^{{\left(M_{t}-{\frac {1}{2}}\langle M\rangle _{t}\right)}},$

ein Martingal. Dies folgt aus dem Kazamaki-Kriterium.

Wichtige Aussagen über Martingale

Ungleichungen

Die wichtigsten Ungleichungen im Bezug auf Martingale sind die Doobsche Maximalungleichung und die Aufkreuzungsungleichung. Die Doobsche Maximalungleichung liefert eine Abschätzung dafür, welcher Maximalwert eines Martingals bis zu einem gegebenen Zeitpunkt nicht überschritten wird. Die Aufkreuzungsungleichung liefert eine Aussage darüber, wie oft ein Submartingal ein vorgegebenes Intervall von unten nach oben durchquert.

Kombination mit Stoppzeiten

Das Optional Stopping Theorem und das Optional Sampling Theorem kombinieren Stoppzeiten mit Martingalen und beschäftigen sich mit den Eigenschaften und Erwartungswerten der gestoppten Prozesse. Mit diesen Ergebnissen kann man zeigen, dass keine Abbruchstrategie für ein faires Spiel existiert, die für den Spieler vorteilhaft ist.

Martingaltransformation

→ Hauptartikel: Martingaltransformation

Ein Martingal und ein vorhersagbarer, lokal beschränkter Prozess lassen sich mittels des diskreten stochastischen Integrals zu einem neuen Martingal kombinieren. Man nennt diesen Prozess dann die Martingaltransformierte des ursprünglichen Martingals. Die Martingaltransformierte ist wieder ein Martingal. Dies hat weitreichende Folgen für die Existenz von Spielstrategien in fairen Spielen, die dem Spieler im Mittel Gewinn bringen. Modelliert das Martingal das faire Spiel und der vorhersagbare, lokal beschränkte Prozess die Spielstrategie, so folgert aus der Martingaltransformation, dass es keine Spielstrategie gibt, die dem Spieler im Allgemeinen einen Vorteil bringt.

Doob-Zerlegung

Die Doob-Zerlegung erlaubt für jeden adaptierten integrierbaren stochastischen Prozess eine Zerlegung in ein Martingal und einen vorhersagbaren Prozess.

Martingalkonvergenzsatz

Der Martingalkonvergenzsatz liefert für Zufallsvariablen, die ein Martingal bilden, Kriterien unter denen sie fast sicher oder im p-ten Mittel konvergieren.

Abgeleitete Prozessklassen

Lokale Martingale

Lokale Martingale sind Prozesse, für die eine monoton wachsende Folge von Stoppzeiten existiert, so dass für jede Stoppzeit der gestoppte Prozess ein Martingal ist.

Semimartingale

Semimartingale sind eine Klasse von adaptierten Prozessen mit Càdlàg-Pfaden (Die Pfade sind rechtsseitig stetig und die linksseitigen Limites existieren), die sich in ein lokales Martingal, ein Prozess mit lokal endlicher Variation und einen fast sicher endlichen Anteil zerlegen lassen.

Rückwärtsmartingale

Rückwärtsmartingale sind Martingale, bei denen die Indexmenge umgekehrt wird. Sie laufen quasi "falschherum" bzw. von hinten nach vorne.

Herkunft des Wortes

Die Martingale ist eine seit dem 18. Jahrhundert bekannte Strategie im Glücksspiel, bei der nach einem verlorenen Spiel der Einsatz erhöht, im einfachsten Fall verdoppelt wird, so dass im hypothetischen Falle unerschöpflichen Vermögens, unerschöpflicher Zeit, und der Nichtexistenz eines Höchsteinsatzes sicherer Gewinn einträte.

Da die Martingale das bekannteste Spielsystem war und ist, wurde der Begriff auch als Synonym für „Spielsystem“ gebraucht und fand so Eingang in die mathematische Literatur.

Das Wort „Martingale“ selbst stammt aus dem Provenzalischen und leitet sich von der französischen Stadt Martigues im Département Bouches-du-Rhône am Rande der Camargue ab, deren Einwohner früher als etwas naiv galten. Der provenzalische Ausdruck jouga a la martegalo bedeutet so viel wie sehr waghalsig zu spielen.

Der „Martingal“ genannte Hilfszügel soll ebenfalls nach der Stadt Martigues benannt sein, hierbei handelt es sich um einen optionalen Teil der Pferdeausrüstung, der das Pferd daran hindern soll, den Kopf nach oben zu reißen und zu steigen. Dass dieser Hilfszügel ebenfalls Martingal genannt wird, war den Pionieren der Martingaltheorie nicht bekannt – und hat mit der mathematischen Begriffsbildung nichts zu tun.

Basierend auf einem Artikel in:

Wikipedia.de