Monte-Carlo-Simulation

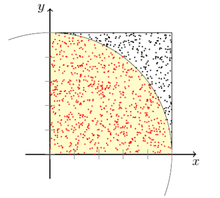
Die Kreiszahl Pi wird mit der Monte-Carlo-Methode angenähert bestimmt durch das Vierfache der Wahrscheinlichkeit, mit der ein innerhalb des Quadrats zufällig gewählter Punkt in den Kreis fällt. Aufgrund des Gesetzes der großen Zahlen sinkt mit steigender Anzahl von Experimenten die Varianz des Ergebnisses.

Monte-Carlo-Simulation oder Monte-Carlo-Studie, auch MC-Simulation, ist ein Verfahren aus der Stochastik, bei dem eine sehr große Zahl gleichartiger Zufallsexperimente die Basis darstellt. Es wird dabei versucht, analytisch nicht oder nur aufwendig lösbare Probleme mit Hilfe der Wahrscheinlichkeitstheorie numerisch zu lösen. Als Grundlage ist vor allem das Gesetz der großen Zahlen zu sehen. Die Zufallsexperimente können entweder – etwa durch Würfeln – real durchgeführt werden oder in Computerberechnungen mittels Monte-Carlo-Algorithmen. Bei Letzteren werden zur Simulation von zufälligen Ereignissen scheinbar zufällige Zahlen berechnet, die auch als Pseudozufallszahlen bezeichnet werden.

Zu den Pionieren der Monte-Carlo-Methode in den 1940er Jahren gehören Stanislaw Ulam, Nicholas Metropolis und John von Neumann. Als grundlegende Veröffentlichung gilt eine Arbeit von Metropolis, Edward Teller, Augusta H. Teller, Marshall Rosenbluth und Arianna W. Rosenbluth von 1953.

Geschichte

Das 1733 von Georges-Louis Leclerc de Buffon vor der Pariser Akademie der Wissenschaften vorgestellte Nadelproblem, das mit Hilfe des Zufalls die nährungsweise Bestimmung der Kreiszahl Pi ermöglicht, war eine der ersten Anwendungen einer Monte-Carlo-Simulation. (→Probabilistische Bestimmung der Zahl Pi)

Enrico Fermi hatte in den 1930er Jahren die eigene Ideen zu Monte-Carlo-Simulationen mittels elektronischer Rechenmaschinen. Ausgeführt wurden diese 1946 von Stanislaw Ulam und dem von ihm deshalb kontaktierten John von Neumann. Dies geschah zur Zeit des 2. Weltkriegs während der Arbeit an einem damals geheimen Projekt am Los Alamos Scientific Laboratory, für das ein Codename nötig war. Es ging im Rahmen der Entwicklung der ersten Atombombe um die Neutronendiffusion in nuklearen Materialien. Auch die mathematische Methode der Simulation musste geheim gehalten werden. Der Name Monte-Carlo wurde von Nicholas Metropolis geprägt und hängt wie folgt mit der Methode zusammen: Stan Ulam hatte einen Onkel, der sich zum Spielen immer Geld von Verwandten geliehen hatte, denn „er musste nach Monte Carlo gehen“. Dies ist natürlich eine Anspielung auf die Spielbank Monte-Carlo im gleichnamigen Stadtteil des Stadtstaates Monaco.

Als grundlegende Veröffentlichung gilt eine Arbeit von Nicholas Metropolis, Marshall N. Rosenbluth und dessen Ehefrau Arianna W. Rosenbluth, Edward Teller und dessen Ehefrau Augusta H. Teller, veröffentlicht 1953 im Journal of Chemical Physics. Ziel war die Berechnung der Zustandsgleichung eines zweidimensionalen Systems starrer Kugeln als Modelle einer Flüssigkeit. Simuliert wurde mit 224 Teilchen und periodischen Randbedingungen. Jede Simulation bestand aus bis zu 48 Zyklen, in denen jeweils jedes Teilchen einen Bewegungsschritt ausführte. Ein Zyklus benötigte drei Minuten auf dem MANIAC I Computer des Los Alamos National Laboratory. Verwendet wurde eine Sampling-Methode mit Wichtung über den Boltzmannfaktor, das Herzstück des MC-Verfahrens im Metropolis-Algorithmus, wobei die Idee nach Marshall Rosenbluth von Teller gekommen sein soll. Nach Rosenbluth leisteten er und seine Frau die Hauptarbeit für den Artikel (Metropolis hätte hauptsächlich Computerzeit zur Verfügung gestellt) und sie waren die einzigen der Autoren, die das Verfahren in anschließenden Publikationen weiterverfolgten, sie wandten sich aber selbst ebenfalls bald darauf anderen Forschungsthemen (Plasmaphysik) zu.

Mathematik

Mathematisch ist das System ein wahrscheinlichkeitsgewichteter Weg im Phasenraum (allgemein Zustandsraum). Monte-Carlo-Simulationen sind besonders geeignet, um statistische Mittelwerte einer Größe ${\mathcal {A}}$ ,

$\left\langle {\mathcal {A}}\right\rangle =\sum _{{x\in \Omega }}P(x)\,{\mathcal {A}}(x),$

oder hochdimensionale Integrale (Monte-Carlo-Integration) wie

$\int _{x\in \Omega }\!\!P(x)\,{\mathcal {A}}(x)\;\mathrm {d} ^{n}x$

zu berechnen. P(x) soll in diesem Zusammenhang ein normiertes statistisches Gewicht (etwa ein Boltzmanngewicht) sein. ${\mathcal {A}}(x)$ ist der Wert der Größe ${\mathcal {A}}$ im Zustand . Die Summation bzw. Integration verläuft hier über einen Raum $\Omega$ , also der Phasenraum der Teilchen im System.

Häufig ist der Raum $\Omega$ so groß, dass die Summation nicht vollständig durchgeführt werden kann. Stattdessen erzeugt man nun eine Markow-Kette $x_{1},x_{2},x_{3},\ldots$ von Zuständen in $\Omega$ , deren Häufigkeit wie das vorgegebene Gewicht P(x) verteilt ist. Bereiche des Raumes $\Omega$ mit hohem Gewicht sollen also häufiger in der Markow-Kette vertreten sein als Bereiche mit niedrigem Gewicht. Man spricht hier von Importance Sampling. Gelingt dies, so lassen sich die Erwartungswerte einfach als arithmetisches Mittel der Größe ${\mathcal {A}}$ zu diesen Zuständen der Markow-Kette berechnen, also als

$\left\langle {\mathcal {A}}\right\rangle \approx {\frac {1}{N}}\sum _{{i=1}}^{N}{\mathcal {A}}(x_{i}).$

Dieser Zusammenhang basiert auf dem Gesetz der großen Zahlen. Je nach physikalischem System kann es schwierig sein, diese Markow-Kette zu erzeugen. Insbesondere ist sicherzustellen, dass die Markow-Kette tatsächlich den gesamten Raum $\Omega$ bedeckt und nicht nur einen Teil des Raumes abtastet. Man sagt: der Algorithmus muss ergodisch sein.

Quasi-Monte-Carlo-Simulationen verwenden keine Pseudozufallszahlen, sondern eine Sequenz mit geringer Diskrepanz (zum Beispiel eine Sobol-Sequenz).

Anwendungen

Anwendungen der Monte-Carlo-Simulation sind beispielsweise:

als Alternative zur analytischen Lösung von Problemen rein mathematischer Herkunft,
- die Approximation der Zahl Pi mit Hilfe des Buffonschen Nadelproblems oder durch die zufällige „Beregnung“ eines Quadrats auf dem Einheitskreis mit Zufallspunkten (hier ist der Anteil der Punkte, die im Einheitskreis liegen, etwa π/4).
- in Verallgemeinerung die Berechnung des Integrals einer Funktion über dem Intervall [0;1] (Flächeninhalt) und dann auch höherdimensionaler Integrale (Volumen).
Verteilungseigenschaften von Zufallsvariablen unbekannten Verteilungstyps,
- die Ermittlung der nichtzentralen Verteilung des Korrelationskoeffizienten. Mit Hilfe von Zufallszahlen wird die Realisierung beliebig vieler Korrelationskoeffizienten simuliert. Eine Zusammenfassung der Koeffizienten in eine Häufigkeitstabelle ergibt eine empirische Verteilungsfunktion.
- die Eigenschaften von Schätzfunktionen bei Vorliegen von Ausreißern in Daten. Mit Hilfe der Simulation kann gezeigt werden, dass das arithmetische Mittel nicht mehr ein bester Schätzer für den Erwartungswert ist.
- die Schätzung von Verteilungsparametern.
die Nachbildung von komplexen Prozessen, die nicht direkt analysiert werden können,
- Produktionsprozesse in einem Fertigungsunternehmen, um Engpässe und Opportunitäten in der Produktion aufzudecken
- Wetter und Klima der Erde.
- Rekonstruktionsverfahren in der Nuklearmedizin.
- Risikoaggregation zur Bestimmung des Gesamtrisikoumfangs eines Unternehmens im Risikomanagement
- Ableitung von Bewertungen in der Wertermittlung, z.B. bei der Unternehmensbewertung oder Immobilienwirtschaft. Bepreisung komplexer Finanzkontrakte wie „exotische“ Optionen, bei denen keine analytische Formel für die Bewertung eines Finanzproduktes bekannt ist.
- räumliche Verteilung des energieabhängigen Neutronenflusses in einem heterogenen Medium, etwa im Blanket eines Kernfusionsreaktors.
- Wege eines einzelnen Regentropfens simulieren, der mit zufällig verteilten anderen Tropfen kollidiert. Nach der Simulation mehrerer konkreter Tropfen sind Aussagen über die durchschnittliche Tropfengröße möglich oder auch zu Temperatur und Tröpfchendichte, bei denen Schnee oder Hagel entstehen.
- Verteilung der Kugeln auf die Fächer beim Galtonbrett.

Mit der Monte-Carlo-Methode können Probleme mit statistischem Verhalten simuliert werden. Diese Methode hat deshalb besonders in der Physik wichtige Anwendungen gefunden, und zwei Bücher des Autors Kurt Binder gehören zu den meistzitierten Veröffentlichungen in dieser Wissenschaftssparte.

Heutige Supercomputer (HPC) basieren auf massivem Multiprocessing mit vielen tausend Einzelprozessoren, die parallel arbeiten. Diese Gegebenheiten lassen sich besonders gut mit solchen probabilistischen Lösungsverfahren ausnutzen. Supercomputer und MC Methoden werden u.a. für die Simulation der alternden Nuklearwaffen der USA benutzt.

Beispiele

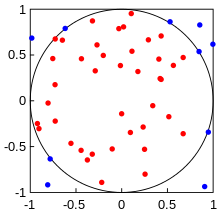
Illustration zur Monte-Carlo-Bestimmung von Pi.

Probabilistische Bestimmung der Zahl Pi

Man wählt hierzu zufällige Punkte $\left(x,y|x\in \left[-1..1\right]\wedge y\in \left[-1..1\right]\right)$ aus und überprüft (durch Anwendung des Satzes von Pythagoras), ob diese innerhalb des Einheitskreises liegen:

$x^{2}+y^{2}\leq 1$ .

Über das Verhältnis der Anzahl der Punkte innerhalb und außerhalb des Kreises kann dann folgendermaßen $\ \pi$ bestimmt werden:

${\frac {{\text{Kreisfl}}\mathrm {\ddot {a}} {\text{che}}}{{\text{Quadratfl}}\mathrm {\ddot {a}} {\text{che}}}}={\frac {r^{2}\cdot \pi }{(2\cdot r)^{2}}}={\frac {\pi }{4}}={\frac {{\text{Treffer in Kreisfl}}\mathrm {\ddot {a}} {\text{che}}}{\text{generierte Punkte im Quadrat}}}=P\left({\text{Im Kreis}}\right)$

Siehe auch: Kreiszahl

Numerische Integration

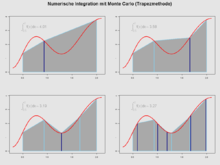
Numerische Integration mit Monte Carlo: Die Stützstellen werden zufällig gleichverteilt auf dem Integrationsintervall gewählt. Neue Stützstellen sind dunkelblau, die alten hellblau eingezeichnet. Der Wert des Integrals nähert sich 3,32 an.

Das obige Beispiel zur Bestimmung von Pi bildet praktisch das Flächenintegral einer Viertelkreisfläche. Entsprechend kann man das Flächenintegral allgemeiner, auch höherdimensionaler Funktionen nach dieser Methode berechnen. Soll das Integral

$S(f)=\int _{0}^{1}f(x)\,dx$

einer Funktion berechnet werden, dann wählt man unabhängige im Intervall [0,1] gleichverteilte Punkte $x_{1},\dots ,x_{m}$ und approximiert S(f) durch

$S_{m}(f)={\frac 1m}\sum _{{i=1}}^{m}f(x_{i}).$

Im allgemeineren Fall von höherdimensionalen Funktionen ist das Vorgehen ähnlich. Sei $K\subset {\mathbb {R}}^{n}$ eine beliebige -dimensionale Menge und $f\colon K\rightarrow \mathbb {R}$ eine integrierbare Funktion. Um den Wert

$S(f)=\int _{K}f(x)\,dx$

näherungsweise zu berechnen, wählt man zufällig in der Menge gleichverteilte Punkte $x_{i}$ für $i=1,\dots,m$ . Dann approximiert

$S_{m}(f)={\frac {{\mathrm {vol}}(K)}{m}}\sum _{{i=1}}^{m}f(x_{i})$

den Wert S(f) in Abhängigkeit von beliebig genau. Um wie oben vorgestellt Pi zu berechnen, muss man $K:=[-1,1]^{2}$ und $f:=\chi _{{{\mathrm {Kreis}}}}$ als charakteristische Funktion des Einheitskreises wählen. Hier ist $S(\chi _{{{\mathrm {Kreis}}}})=\pi$ gerade die Fläche des Einheitskreises.

In der Praxis werden Monte-Carlo Verfahren vor allem für die Berechnung hochdimensionaler Integrale verwendet. Hier sind klassische Integrationsalgorithmen stark vom Fluch der Dimensionalität betroffen und nicht mehr anwendbar. Allerdings sind speziell hochdimensionale Integranden meist stark lokalisiert. In diesen Fällen erlauben insbesondere MCMC-Verfahren die Erzeugung von Stichproben mit einer Verteilung die eine effiziente Berechnung solcher hochdimensionaler Integrale erlaubt.

Miller-Rabin-Primzahltest

Ein Beispiel für einen Monte-Carlo-Simulation ist der Miller-Rabin-Test, bei dem probabilistisch bestimmt wird, ob eine natürliche Zahl prim ist oder nicht. Die Ausgabe des Tests lautet entweder „sicher zusammengesetzt“ oder „wahrscheinlich prim“. Die Wahrscheinlichkeit, dass eine zusammengesetzte Zahl als „wahrscheinlich prim“ klassifiziert wird, liegt pro Durchgang unter 25 % und kann durch mehrfache Ausführung weiter gesenkt werden. Der Miller-Rabin-Test liefert keine Aussage über die Faktoren einer zusammengesetzten Zahl, ist also kein Faktorisierungsverfahren.

Programmpakete

MCNP, der Monte-Carlo N-Particle Transport Code, ist ein prototypisches, weltweit verbreitetes reaktorphysikalisches Programm, das sehr häufig angewendet wird, auch in der Kerntechnik und der Kernfusionstechnik. Die aktuelle Version ist MCNP6.2. Auf der MCNP-Webseite sind Handbücher und Release Notes als Internetdokumente zu finden, zum Beispiel der Band I des MCNP-Handbuchs Overview and Theory.

PYTHIA ist ein Simulationsprogramm für die Teilchenphysik und simuliert Kollisionen und dabei entstehende Teilchen.

SHERPA ist ein Simulationsprogramm für die Hochenergie-Teilchenphysik. Entstanden an der TU Dresden, wird es inzwischen von einer international verteilten Arbeitsgruppe um Frank Krauss entwickelt.

SPICE ist ein Simulationsprogramm für analoge, digitale und gemischte elektronische Schaltungen. Mit der Monte-Carlo-Simulation ist es möglich, die Auswirkungen der Streuung der Bauteilewerte innerhalb der angegebenen Toleranz zu berechnen.

Literatur

Kurt Binder: Monte Carlo methods in statistical physics. Springer, Berlin [u.a.] 1979, ISBN 3-540-09018-5.
Kurt Binder: Applications of the Monte Carlo method in statistical physics. Springer, Berlin 1984, ISBN 3-540-12764-X.
Paul Glasserman: Monte Carlo Methods in Financial Engineering. Springer, Berlin 2003, ISBN 978-1-4419-1822-2.
David P. Landau, Kurt Binder: A guide to Monte Carlo simulations in statistical physics. Cambridge University Press, Cambridge, 2014, ISBN 978-1107074026

Basierend auf einem Artikel in:

Wikipedia.de