A5 (Gruppe)
Die im mathematischen Teilgebiet der Gruppentheorie
betrachtete Gruppe
ist die alternierende
Gruppe 5-ten Grades. Sie hat 60 Elemente und ist die kleinste nichtabelsche einfache
Gruppe und die kleinste nicht-auflösbare
Gruppe. Sie findet eine geometrische Realisierung als Gruppe der Rotationen
des Ikosaeders.
Definitionen
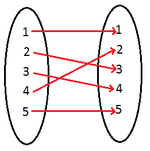
Wir betrachten die Menge aller bijektiven Abbildungen der
5-elementigen Menge
in sich. Diese bildet mit der Hintereinanderausführung
von Abbildungen als Verknüpfung eine Gruppe;
man nennt diese Verknüpfung auch Produkt und schreibt sie als
oder ganz ohne Verknüpfungszeichen. Dies ist die symmetrische Gruppe
mit
Elementen.
Solche Abbildungen nennt man Permutationen
und verwendet für sie die sogenannte Zykelschreibweise
mit verschiedenen Elementen
.
Die Abbildung
bildet jedes Element in der Zykelliste auf das rechts neben ihm stehende ab und
schließlich das letzte der Liste auf das erste. Der Zykel
bildet also 2 auf 3, 3 auf 4 und 4 auf 2 ab und lässt die Elemente 1 und 5 fest.
Ein Zykel
der Länge 2 vertauscht demnach nur
und
und lässt alle anderen Elemente fest, solche Abbildungen nennt man Transpositionen.
Verschiedene Zykel können dieselbe Permutation beschreiben, es gilt etwa
,
Eindeutigkeit erhält man durch die Vereinbarung, die kleinste im Zykel
vorkommende Zahl an den Anfang zu stellen.
Man kann jede Permutation als Produkt von Zykeln schreiben, sogar als Produkt von Transpositionen. Die Darstellung als Produkt von Transpositionen ist nicht eindeutig. Siehe zum Beispiel
Wir verwenden hier die bei Abbildungen übliche Reihenfolge, das heißt zuerst
wird die Abbildung
angewendet, dann
.
(Das wird in der Literatur nicht einheitlich so gehandhabt; Autoren, die
Operationen und Funktionen auf die rechte Seite der abzubildenden Elemente
schreiben, verwenden hier genau die umgekehrte Konvention.) Eindeutig ist aber,
ob für die Darstellung einer Permutation als Produkt von Transpositionen eine gerade
oder ungerade Anzahl von Transpositionen erforderlich ist, entsprechend
nennt man die Permutationen gerade oder ungerade.
Dann ist klar, dass das Produkt von geraden Permutationen wieder gerade ist,
denn die Anzahlen der verwendeten Transpositionen addieren sich bei der
Verknüpfung. Die geraden Permutation bilden daher eine Untergruppe, das ist die
alternierende Gruppe .
Selbstverständlich sind analoge Begriffsbildungen für
an Stelle von
möglich, das führt dann zur alternierenden
Gruppe An. In diesem Artikel behandeln wir den Fall
.
Elementare Eigenschaften
Anzahl der Elemente
Ist
irgendeine Permutation, so ist
genau dann gerade bzw. ungerade, wenn
ungerade bzw. gerade ist. Also gibt es genauso viele gerade wie ungerade
Permutationen und daraus folgt, dass
60 Elemente hat.
Dreierzykel
Ein Dreierzykel, das heißt ein Zykel
der Länge drei, ist gerade, denn
.
Ein Dreierzykel
ist offenbar eine Abbildung, die jedes der Elemente aus
auf ein jeweils anderes Element dieser Dreiermenge abbildet und die anderen
beiden Elemente aus
fest lässt; davon gibt es genau zwei solcher Abbildungen, nämlich
und
.
Da es insgesamt
solcher Dreiermengen gibt, kommen wir insgesamt auf 20 Dreierzykel. Da
umgekehrt
für
paarweise verschieden
für
paarweise verschieden,
ist jede gerade Permutation ein Produkt von Dreierzykeln, das heißt die
Gruppe
wird von den Dreierzyklen erzeugt.
Ordnungen
Wie in jeder Gruppe gibt es genau ein Element der Ordnung 1, nämlich das neutrale Element.
Die Elemente der Ordnung 2 erhält man aus Transpositionen, die ja offenbar
die Ordnung 2 haben. Da
nur gerade Permutationen enthält, sind die Permutationen der Ordnung 2 genau die
Produkte aus zwei elementfremden Transpositionen
mit paarweise verschiedenen
.
Es gibt 5 Möglichkeiten für eine Vierermenge
(jeweils ein Element gehört nicht dazu) und zu jeder solchen Vierermenge kann
man die drei verschiedenen Elemente
der Ordnung 2 bilden, das macht insgesamt
Elemente der Ordnung 2.
Die Elemente der Ordnung 3 sind die oben erwähnten 20 Dreierzykel.
Alle Fünferzykel
sind Produkte aus zwei Dreierzykel und daher Elemente der
und haben offenbar die Ordnung 5. Da alle 5 Zahlen in
vorkommen, ist auch die 1 dabei, die man an die erste Stelle setzt. Es gibt
daher genau die Fünferzykel
mit paarweise verschiedenen
,
und dazu gibt es
Möglichkeiten. Es gibt demnach 24 Elemente der Ordnung 5.
Damit haben wir die Ordnungen von 1+15+20+24 = 60 Elementen bestimmt, es gibt also keine Elemente weiterer Ordnungen. Wir erhalten damit folgende Übersicht:
| Ordnung | Anzahl | Typisches Element | Beschreibung |
|---|---|---|---|
| 1 | 1 | neutrales Element | |
| 2 | 15 | zwei elementfremde Transpositionen | |
| 3 | 20 | Dreierzykel | |
| 5 | 24 | Fünferzykel |
Präsentation
Eine Präsentation
durch Erzeugende und Relationen sieht so aus: Die Gruppe
wird durch zwei Erzeugende
und die Relationen
definiert. Das heißt jede Gruppe, die von zwei Elementen
erzeugt wird, die zusätzlich die genannten Relationen erfüllen, ist isomorph zu
.
Die
selbst ist von
und
erzeugt, und diese Elemente erfüllen die angegebenen Relationen.
Transitive Operation auf 6 Elementen
Die Gruppe
hat 24 Elemente der Ordnung 5, von denen jeweils 4 zusammen mit dem neutralen
Element eine Untergruppe der Ordnung 5 bilden, es gibt daher sechs Untergruppen
der Ordnung 5, die gleichzeitig die 5-Sylowgruppen sind. Da die
Gruppe mittels Konjugation
transitiv
auf den sechs 5-Sylowgruppen operiert,
denn je zwei 5-Sylowgruppen sind konjugiert, erhalten wir insgesamt, dass
transitiv auf einer sechselementigen Menge operiert. Diese Operation ist sogar
treu.
Hiervon gilt folgende Umkehrung:
- Jede 60-elementige transitive Permutationsgruppe auf 6 Elementen ist
isomorph zu
.
A5 ist nicht auflösbar
Zu einer beliebigen Gruppe
ist die Kommutatorgruppe
definiert als die von allen Kommutatoren
erzeugte Untergruppe. Induktiv erklärt man
und nennt die Gruppe auflösbar,
wenn es ein
gibt mit
.
Die Gruppe
ist nicht auflösbar. Ist nämlich
ein Dreierzykel, so seien
die beiden nicht darin vertretenen Zahlen aus
.
Dann rechnet man
,
das heißt, jeder Dreierzykel ist ein Kommutator und daher aus .
Da die Dreierzykel nach obigem die Gruppe
erzeugen, folgt
und damit
für alle
.
Daher ist
nicht auflösbar.
ist die kleinste nicht auflösbare Gruppe. Bekanntlich ist jede p-Gruppe, das heißt Gruppe der
Ordnung
für eine Primzahl
,
auflösbar. Ferner sind Gruppen der Ordnung
mit Primzahlen
und
nach dem Satz
von Burnside auflösbar. Schließlich sind Gruppen der Ordnung
mit Primzahlen
und
auflösbar.
Die kleinste Ordnung, die für eine nicht-auflösbare Gruppe überhaupt in Frage
kommt, ist damit
.
ist daher eine nicht-auflösbare Gruppe kleinstmöglicher Ordnung, man kann sogar
zeigen dass sie bis auf Isomorphie die einzige nicht-auflösbare Gruppe der
Ordnung 60 ist.
Aus der Nicht-Auflösbarkeit von
ergibt sich leicht, dass alle
und alle
mit
nicht auflösbar sind, denn Untergruppen auflösbarer Gruppen sind wieder
auflösbar und all diese Gruppen enthalten eine zu
isomorphe Untergruppe.
A5 ist einfach
Eine Gruppe
heißt einfach, wenn sie neben den trivialen Normalteilern
und
keine weiteren Normalteiler enthält. Da Kommutatorgruppen Normalteiler sind,
haben auflösbare Gruppen, die nicht zyklisch
von Primzahlordnung sind, stets Normalteiler, aber auch nicht-auflösbare Gruppen
können Normalteiler haben, wie das Beispiel
zeigt, die
als Normalteiler hat. Daher ist folgende Aussage eine Verschärfung der
Nicht-Auflösbarkeit:
ist einfach.
Das ergibt sich leicht aus der Tatsache, dass
eine nicht-auflösbare Gruppe kleinstmöglicher Ordnung ist. Wäre nämlich
ein nicht-trivialer Normalteiler, so hätten
und
eine echt kleinere Ordnung und wären daher auflösbar. Aus den bekannten Sätzen
über auflösbare Gruppen folgte daraus die Auflösbarkeit von
,
was den gewünschten Widerspruch ergibt.
Das gerade gegebene Argument für die Einfachheit der
ist durchaus nicht-trivial, denn es verwendet den Satz von Burnside, der in der
Minimalität von 60 für die Ordnung einer nicht-auflösbaren Gruppe steckt.
Allerdings benötigt man den Satz von Burnside nicht in voller Stärke, die ohne
Darstellungstheorie
zu beweisende Auflösbarkeit von Gruppen der Ordnung
mit
ist ausreichend.
In einem einfacheren Beweis zeigt man zunächst, dass alle Dreierzykel konjugiert
sind und anschließend, dass jeder von der einelementigen Untergruppe
verschiedene Normalteiler mindestens einen Dreierzykel enthalten muss. Der
Normalteiler enthält dann alle Konjugierten dieses Dreierzykels, denn
Normalteiler sind ja definitionsgemäß unter Konjugation stabil, und daher alle
Dreierzykel. Da diese aber bereits
erzeugen, folgt
,
das heißt es gibt keine nicht-trivialen Normalteiler in
.
Dieser Beweis gilt für alle
.
Ein weiterer einfacherer und auf die
zugeschnittener Beweis unter Verwendung der Sylow-Sätze
findet sich im unten angegebenen Lehrbuch von B. Huppert.[1]
Darüber hinaus wird dort gezeigt:
- Ist
eine einfache Gruppe der Ordnung 60, so ist
.
Charaktertafel
Die Charaktertafel
der
sieht wie folgt aus:
Vorkommen
Symmetriegruppe
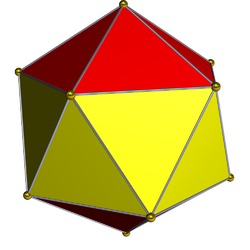
Die
tritt als Rotationsgruppe des Ikosaeders
auf, daher nennt man sie auch die Ikosaedergruppe.
Um einen Überblick über die möglichen Rotationen, die den Ikosaeder in sich
überführen, zu erhalten, betrachten wir, wie sie sich auf die Kanten auswirken.
Die 30 Kanten des Ikosaeders zerfallen in 5 Klassen paralleler Kanten, wobei
jede dieser Klasse 6 parallele Kanten enthält. Da Rotationen des Ikosaeders
Parallelität von Kanten erhalten müssen, permutieren sie diese 5 Klassen und man
erhält einen Homomorphismus von der Ikosaedergruppe in die
.
Eine genauere Betrachtung zeigt dann, dass es sich um einen injektiven
Homomorphismus handelt, dessen Bild gerade
ist. Daher ist die Ikosaedergruppe isomorph zur
.
Die Elemente der
entsprechen damit folgenden Drehungen:
Die 30 Kanten bestimmen 15 Rotationsachsen durch die Mittelpunkte von Paaren
gegenüberliegender Kanten, und um jede Achse ist eine Rotation um
möglich. Das sind die 15 Elemente der Ordnung 2.
Die 20 Seitenflächen bestimmen 10 Rotationsachsen durch die Mittelpunkte von
Paaren gegenüberliegender Seitenflächen, und um jede dieser Achsen ist eine
Rotation um
oder
möglich, das sind die 20 Elemente der Ordnung 3.
Die 12 Ecken bestimmen 6 Rotationsachsen durch Paare gegenüberliegender
Ecken, zu jeder Achse gibt es 4 Drehungen um ,
der Ordnung 5, das sind insgesamt die 24 Drehungen der Ordnung 5.
Galoisgruppe
Das Polynom
hat eine zur
isomorphe Galoisgruppe.
Nach Sätzen der Galoistheorie
bedeutet das wegen der oben festgestellten Nicht-Auflösbarkeit der Gruppe, dass
die Nullstellen des Polynoms nicht durch Radikale der Koeffizienten dargestellt
werden kann. Das belegt den Satz
von Abel-Ruffini, nach dem es für Polynome ab dem Grad 5 keine allgemeinen
Lösungsformeln gibt, die aus Wurzeln und arithmetischen Operationen der
Koeffizienten bestehen.
PSL2(4) und PSL2(5)
Die projektiven
linearen Gruppen
für einen endlichen Körper
mit
Elementen sind mit Ausnahme von
und
einfach und haben
Elemente. Demnach gilt
.
Da alle einfachen Gruppen der Ordnung 60 wie oben erwähnt isomorph zur
sind, folgt
.
Literatur
- ↑ B. Huppert: Endliche Gruppen I. Springer-Verlag, 1967, Kapitel I, Satz 8.14.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 20.01. 2020