Thermodynamisches Potential

Thermodynamische Potentiale sind in der Thermodynamik Größen, die von ihrem Informationsgehalt her das Verhalten eines thermodynamischen Systems im Gleichgewicht vollständig beschreiben. Die unabhängigen Zustandsvariablen eines thermodynamischen Potentials bezeichnet man dann als dessen natürliche Variablen, wenn deren Ableitung des Potentials gleich einer der abhängigen Zustandsvariablen ist (beispielsweise: $\left(\partial U/\partial S\right)_{V,N}=T$ ). Ein thermodynamisches Potential entspricht vom Informationsgehalt der inneren Energie , deren natürliche Variablen S,V,N alle extensiv sind (Fundamentalgleichung).

Thermodynamische Potentiale, die Energien sind, lassen sich durch Legendre-Transformation aus der inneren Energie U(S,V,N) herleiten, haben jedoch anders als diese eine oder mehrere intensive Größen als natürliche Variablen $(T, p, \mu)$ . Die intensiven Größen entstehen bei der Koordinatentransformation als Ableitungen der inneren Energie nach ihren extensiven Variablen.

Daneben gibt es weitere thermodynamische Potentiale, die keine Energien sind, beispielsweise die Entropie S(U,V,N) .

Der Begriff des thermodynamischen Potentials wurde von Gottfried Falk zum Begriff der Massieu-Gibbs-Funktionen (nach Josiah Willard Gibbs) verallgemeinert, bei denen es sich um entsprechende Zustandsfunktionen in nicht notwendigerweise thermodynamischen Systemen handelt.

Physikalische Bedeutung

Ein Extremwert (nicht immer ein Minimum) eines thermodynamischen Potentials zeigt das thermodynamische Gleichgewicht an.

So hat sich nach dem Anschluss eines abgeschlossenen Systems an ein anderes ein thermodynamisches Gleichgewicht eingestellt, sobald die Entropie des Gesamtsystems maximal ist. In diesem Fall sind auch alle intensiven Parameter der beiden Systeme jeweils gleich:

$\begin{align} T_1 & = T_2\\ p_1 & = p_2\\ \mu_1 & = \mu_2 \end{align}$

Außerdem fassen thermodynamische Potentiale die Zustandsgleichungen des Systems zusammen, da diese durch Differenzieren eines thermodynamischen Potentiales nach seinen abhängigen Variablen zugänglich sind.

Beschreibung

Die innere Energie U(S,V,N) und die aus ihr mittels Legendre-Transformation hervorgehenden Funktionen sind thermodynamische Potentiale (bis auf die Ausnahme , s.u.). Die Legendre-Transformation transformiert die Potentiale

von Entropie nach Temperatur , da ${\frac {\partial U}{\partial S}}=T$
von Volumen nach Druck , da ${\frac {\partial U}{\partial V}}=-p$
von Teilchenzahl nach chemisches Potential $\mu$ , da ${\frac {\partial U}{\partial N}}\,=\mu$

Aufgrund dieser 3 Variablenpaare gibt es 2^3 = 8 mögliche thermodynamische Potentiale:

Thermodynamische Potentiale
Name (Alternativname)	Formelzeichen	natürliche Variablen (intensive fett)	Charakteristische Funktion f	Zusammenhänge
Innere Energie			${\mathrm d}U=TdS-pdV+\mu {d}N$	$U(S,V,N)=TS-pV+{\sum _{{i=1}}^{{K}}}\,\mu _{i}N_{i}.$ (Eulergleichung für die innere Energie)
Freie Energie (Helmholtz-Potential)		$\boldsymbol{T},V,N$	${\mathrm d}F=-SdT-pdV+\mu {d}N$
Enthalpie		$S,\boldsymbol{p},N$	${\mathrm d}H=TdS+Vdp+\mu {d}N$	$H=U(S,V,N)\qquad \ +pV$
Gibbs-Energie (Freie Enthalpie)		$\boldsymbol{T},\boldsymbol{p},N$	${\mathrm d}G=-SdT+Vdp+\mu {d}N$	${\begin{aligned}G&=U(S,V,N)-TS+pV\\&=H(S,p,N)-TS\\&=F(T,V,N)\qquad \quad +pV\end{aligned}}$
-		$S,V,\boldsymbol{\mu}$	${\mathrm d}R=TdS-pdV-N{d}\mu$	$R=U(S,V,N)\qquad \qquad \quad -\mu N$
Großkanonisches Potential	$\Omega$	$\boldsymbol{T},V,\boldsymbol{\mu}$	${\mathrm d}\Omega =-S{d}T-p{d}V-N{d}\mu$	${\begin{aligned}\Omega &=U(S,V,N)-TS\qquad \ -\mu N\\&=R(S,V,\mu )-TS\\&=F(T,V,N)\qquad \qquad \quad -\mu N\end{aligned}}$
-		$S,\boldsymbol{p},\boldsymbol{\mu}$	${\mathrm d}J=TdS+Vdp-N{d}\mu$	${\begin{aligned}J&=U(S,V,N)\qquad \quad +pV-\mu N\\&=R(S,V,\mu )\qquad \quad +pV\\&=H(S,p,N)\qquad \quad \qquad -\mu N\end{aligned}}$
-		$\boldsymbol{T},\boldsymbol{p},\boldsymbol{\mu}$ Nicht sinnvoll, da die Gibbs-Duhem-Relation die unabhängige Vorgabe der Variablen $T,p,\mu$ verbietet.	${\mathrm d}K=-SdT+Vdp-N{d}\mu$	${\begin{aligned}K&=U(S,V,N)-TS+pV-\mu N=0\\&=J(S,p,\mu )-TS\\&=\Omega (T,V,\mu )\qquad \quad +pV\\&=G(T,p,N)\qquad \quad \qquad -\mu N\end{aligned}}$

Guggenheim-Quadrat

Alle sinnvollen thermodynamischen Potentiale, die aus U(S,V,N) durch Legendre-Transformation hervorgehen, liefern die gleiche, vollständige Information über ein System. Die einfachste Beschreibung des Systems liefert jedoch je nach Ensemble nur eines der Potentiale; dies ist im Gleichgewicht extremal.

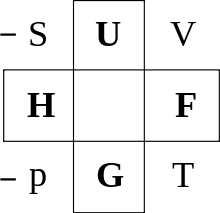
Eine Möglichkeit, sich die thermodynamischen Potentiale mit ihren natürlichen Variablen zu merken, ist das Guggenheim-Quadrat.

Beispiel für Transformation

Exemplarisch soll der Wechsel von einem Potential zum anderen mittels charakteristischer Funktionen (totaler Differentiale) durchgeführt werden.

Ziel ist, von der inneren Energie U mit den natürlichen Variablen S,V,N auf ein neues Potential mit den natürlichen Variablen T,V,N zu transformieren. Wir beginnen bei der inneren Energie:

${\begin{aligned}{\mathrm {d}}U(S,V,N)&={\frac {\partial U}{\partial S}}\,{\mathrm {d}}S+{\frac {\partial U}{\partial V}}\,{\mathrm {d}}V+{\frac {\partial U}{\partial N}}\,{\mathrm {d}}N\\&=T\,{\mathrm {d}}S-p\,{\mathrm {d}}V+\mu \,{\mathrm {d}}N\end{aligned}}$

Mit

${\begin{aligned}{\mathrm {d}}(TS)&=T\,{\mathrm {d}}S+S\,{\mathrm {d}}T\\\Leftrightarrow T\,{\mathrm {d}}S&={\mathrm {d}}(TS)-S\,{\mathrm {d}}T\end{aligned}}$

folgt

$\Rightarrow {\mathrm {d}}U={\mathrm {d}}(TS)-S\,{\mathrm {d}}T-p\,{\mathrm {d}}V+\mu \,{\mathrm {d}}N.$

Nun bringe ${\mathrm {d}}(TS)$ auf die linke Seite:

${\begin{aligned}\Leftrightarrow {\mathrm {d}}(U-TS)&=-S\,{\mathrm {d}}T-p\,{\mathrm {d}}V+\mu \,{\mathrm {d}}N=:{\mathrm {d}}F\\&={\frac {\partial F}{\partial T}}\,{\mathrm {d}}T+{\frac {\partial F}{\partial V}}\,{\mathrm {d}}V+{\frac {\partial F}{\partial N}}\,{\mathrm {d}}N\end{aligned}}$

Das neue Potential U-TS hängt nun von den natürlichen Variablen T,V,N ab und wird „freie Energie “ genannt. Es ist die Legendretransformierte von U(S,V,N) bezüglich der Variablen S.

Zustandsgleichungen

→ Hauptartikel: Zustandsgleichung

Sei $\Phi$ ein beliebiges thermodynamisches Potential, dann kann sein totales Differential geschrieben werden als

$\mathrm{d}\Phi = \sum_i x_i \cdot \mathrm{d}y_i$

wobei

$y_{i}$ die natürlichen Variablen von $\Phi$ sind und
$x_{i}$ die jeweils dazu konjugierten Variablen.

Aus der Kettenregel folgt:

$x_j = \frac{\partial \Phi}{\partial y_j} \Bigg|_{\{y_{i\ne j}\}}$

Hier ist $\{y_{{i\neq j}}\}$ die Menge aller natürlichen Variablen von $\Phi$ ohne $y_{{i}}$ . Die $x_{j}$ sind Ausdrücke thermodynamischer Parameter in Abhängigkeit von Ableitungen des thermodynamischen Potentials, das von seinen natürlichen Variablen abhängt. Die $x_{j}$ sind also gerade die Zustandsfunktionen des Systems.

Literatur

Ulrich Nickel: Lehrbuch der Thermodynamik. Eine anschauliche Einführung. 3., überarbeitete Auflage. PhysChem, Erlangen 2019, ISBN 978-3-937744-07-0.
Christoph Strunk: Moderne Thermodynamik. Von einfachen Systemen zu Nanostrukturen. de Gruyter, Berlin u. a. 2015, ISBN 978-3-11-037105-5.

Basierend auf einem Artikel in:

Wikipedia.de