Digitale Messtechnik

Die Messtechnik kann nach verschiedenen Gesichtspunkten gegliedert werden. Eine Möglichkeit besteht in der Unterscheidung nach analoger oder digitaler Messtechnik. Spezifische Teilgebiete der digitalen Messtechnik sind ihre Messmethode, die Informationsdarstellung und die Gerätetechnik.

Grundlagen – Definitionen – Vergleiche

Messmethoden

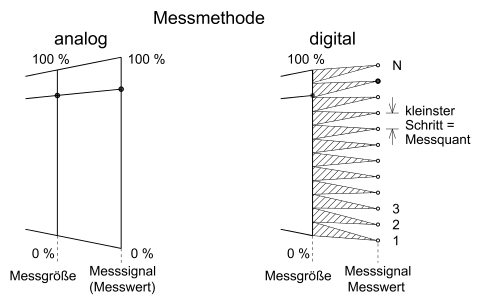
Die Messung ist das Ausführen von geplanten Tätigkeiten zum quantitativen Vergleich der Messgröße mit einer Einheit (DIN 1319-1, Nr. 2.1). Was es ausmacht, wenn dieses Messen ein digitales ist, soll durch den Vergleich mit dem analogen Messen beschrieben werden.

Analoge Messmethode

Sprachliche Grundlage: analog = entsprechend.
Der Messwert wird durch ein Analogon dargestellt, einen ähnlichen oder entsprechenden (analogen) Sachverhalt, hier durch eine Zwischengröße, deren Wert leicht als Zahl ablesbar ist. ¹)

Beispiel: Drehspul-Strommessgerät: Der Strom bewirkt die Verschiebung einer Marke auf einer Skale. Abgelesen wird die Länge oder der Winkel, welche kontinuierlich dem Strom zugeordnet sind.

Jedes Messgerät hat eine Messgeräteabweichung als Folge der Unvollkommenheit der Konstruktion, Fertigung und Justierung, beschreibbar durch

Garantiefehlergrenzen (Ein geringerer Wert ist möglich durch Korrektur mit einer Kurve der Messabweichungen, die aus dem Unterschied zu besseren Geräten oder einem anderen Vergleichsmaßstab bestimmt worden sind),
Messunsicherheit (Ein geringerer Wert ist möglich durch feinere Skalenteilung, größere experimentelle Erfahrung sowie wiederholtes Messen).

Sieht man, um das Wesentliche zu erkennen, von diesen Abweichungen ab, so erkennt man als Merkmale:

Das Ausgangssignal (Strecke oder Winkel) ist beliebig fein auflösbar.
Es ist ein eindeutig umkehrbares Maß für das Eingangssignal.

Weitere Beispiele analoger Messmethoden:

Temperatur: Ausdehnung der thermometrischen Flüssigkeit
Druck: Verformung einer Membran
Drehzahl: Spannung eines Tachogenerators

Das Messgerät verschafft das Analogon, der Beobachter bestimmt daraus den Zahlenwert und zusammen mit der Einheit den Messwert.

¹) Dieser Satz ist nur als anschaulicher Einstieg zu verstehen.

Digitale Messmethode

Sprachliche Grundlage: digit(us) = Finger, Ziffer. ²)
Der Messwert wird direkt in Ziffernform dargestellt. ¹)

Beispiel Drehzahlmesser

Ein Gerät, das

pro Umdrehung ein Zählwerk um eine Eins weiterstellt und
die Zählung genau eine Minute lang zulässt.

Der Zählerstand liefert direkt den Messwert zur Einheit Umdrehung pro Minute.
Anmerkung: Der besondere Name Umdrehung wird als Einheit bei der Spezifikation für drehende Maschinen weitverbreitet verwendet statt der Eins. Entsprechend sind bei der Drehzahl die Einheiten Umdrehung durch Sekunde oder Umdrehung durch Minute weitverbreitet.

Digitale Wheatstone-Brücke

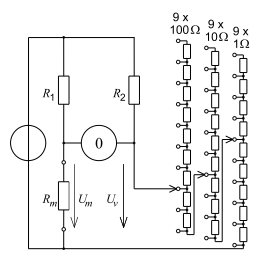
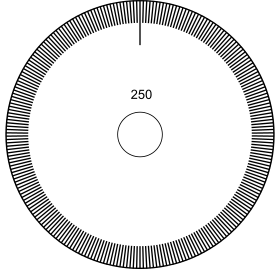
Beispiel Wheatstone-Brücke

Einstellung der Widerstands-Dekaden bis zum „Nullabgleich“, genauer gesagt bis

$-U_{q}/2\leq U_{m}-U_{v}\leq U_{q}/2$ .

Dabei ist $U_{q}$ der kleinste an $U_{v}$ einstellbare Spannungsschritt. Wenn $R_{1}=R_{2}$ ist, dann ist nach dem Abgleich der zu messende Widerstand $R_{m}$ gleich dem an den Dekaden-Schaltern eingestellten Widerstand. Im Bild wird abgelesen:

$R_{m}$ = ganze Zahl mal kleinste Schrittweite = 235 × 1 Ω.

Auch hier sind Messgeräteabweichungen zu beachten,

Garantiefehlergrenzen durch die Fehlergrenzen des eingebauten Vergleichsmaßstabes,
- im Beispiel Zähler: des Zeitmaßstabes,
- im Beispiel Brücke: der verwendeten Widerstände,
Messunsicherheit durch einen Ziffernschritt auf der niederwertigsten Stelle. Diese Quantisierungs- oder Digitalisierungsabweichung kann als relative Abweichung immer dann unbedeutend klein gemacht werden, wenn es gelingt, mit großen Zahlen zu arbeiten, siehe nachfolgend „Zur Quantisierungsabweichung“.

Sieht man, um das Wesentliche zu erkennen, von diesen Abweichungen ab, so erkennt man als Merkmale:

Das Ausgangssignal ist in abzählbar viele Schritte unterteilbar.
Es ist eine in sich eindeutige Aussage.

Die Messgröße kann beliebig feinen Änderungen unterliegen, durch das Messgerät wird ihr Messwert quantisiert,

im Beispiel Zähler: der Wert der Drehzahl durch den Impulsgeber,
im Beispiel Brücke: der Wert des Widerstandes $R_{m}$ durch die schrittweise Einstellung des Vergleichswiderstandes.

¹) Dieser Satz ist nur als anschaulicher Einstieg zu verstehen.

²) Der Begriff Digit wird in der Literatur nicht einheitlich verwendet, oft im Sinne von Ziffernschritt, gelegentlich im Sinne von Stelle.

Zur Quantisierungsabweichung

Es gelingt, zu einer großen Zahl des Messwertes und damit zu einer kleinen relativen Quantisierungsabweichung zu kommen,

im Beispiel Zähler, wenn man mehrere Impulsgeber verwendet, z.B.100 Impulse pro Umdrehung,
im Beispiel Brücke, wenn man den einstellbaren Vergleichs-Widerstand feiner unterteilt, z.B. noch Widerstandsdekaden mit Schrittweiten 0,1 Ω und 0,01 Ω hinzufügt.

Damit erreicht man eine höhere Ablesegenauigkeit, in den beiden Beispielen durch 2 zusätzliche Stellen.
Bei 5 Dezimalstellen ist die relative Quantisierungsabweichung = 1/10000 … 1/99999 = 10⁻⁴ … 10⁻⁵. Ob die Gesamtgenauigkeit damit größer geworden ist, ist zumindest fraglich. Durch die Eindeutigkeit der Ablesung wird allzu leicht vergessen, die übrigen Quellen für Messabweichungen zu beachten. Wenn in der Brücke jeder Widerstand die relative Fehlergrenze von 10⁻³ hat, dann ist auch die relative Fehlergrenze des Ergebnisses nicht kleiner, und die Angabe von 5 Stellen wäre nicht vertretbar. Außerdem müsste beim Messaufbau an die Vermeidung systematischer Abweichungen (Klemmenwiderstände, Thermospannungen) besonders sorgfältig gedacht werden.

Definitionen

Zur Erläuterung der Definitionen der Messmethoden

Definition der analogen Messmethode aus DIN 1319-2:

Messmethode, bei welcher der Messwert durch stufenlose Verarbeitung des Messsignals ermittelt wird.

Definition der digitalen Messmethode aus DIN 1319-2:

Messmethode, bei welcher der Messwert durch stufenweise Verarbeitung des Messsignals ermittelt wird.

Das entscheidende Kennzeichen:

Das Messsignal ist zumindest im Idealfall eine eindeutig umkehrbare Abbildung der Messgröße.

(Gegensatz: Bei der digitalen Messmethode ist ein Rückschluss innerhalb der Breite eines Ziffernschrittes ungewiss.)

Das entscheidende Kennzeichen:

Das Messsignal ist eine in fest gegebenen Schritten quantisierte Abbildung der Messgröße.

(Gegensatz: Bei der analogen Messmethode kann sich das Messsignal beliebig fein einstellen.)

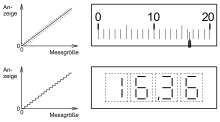
Zur Erläuterung der bevorzugten Anzeigen

Anzeige der Messwerte

Skalenanzeige, Ziffernanzeige

Ziffernanzeige mit Skale zur Ablesung von Zwischenwerten unterhalb des niederwertigsten Ziffernschritts

Bei analog arbeitenden Messgeräten wird die Skalenanzeige bevorzugt.
Bei digital arbeitenden Messgeräten wird die Ziffernanzeige bevorzugt.

Aber eine Fehldeutung wäre:

Skalenanzeige bedeutet analoge Messmethode.

Gegenbeispiel: Zeitmessung; Bahnhofsuhren, die Skalen verwenden, wobei sich der Minutenzeiger schrittweise weiterdreht.

Ziffernanzeige bedeutet digitale Messmethode.

Gegenbeispiel: Energiemessung; elektromechanische Energiezähler, die Ziffernrollen verwenden, wobei sich die Rolle für die letzte Stelle kontinuierlich weiterdreht und mit einer Skale für noch weitergehende Auflösung versehen ist.

Bandanzeige, Balkenanzeige

Bandanzeige mit 51 Segmenten

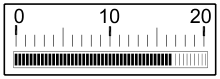
Die Bandanzeige enthält eine Reihe von Segmenten (typisch 5 … 200 Segmente), von denen bei steigender Messgröße eine steigende Anzahl eingeschaltet wird. Sie arbeitet digital und verbindet die Digitaltechnik mit den Vorteilen einer Skalenanzeige. Mit ≥ 100 Segmenten fällt die Stufung kaum mehr auf, und man spricht von quasianalog. Die Balkenanzeige auf einem Bildschirm entspricht auch einer Skalenanzeige, wobei sich die Länge des Balkens mit der Zahl der Bildpunkte so fein stufen lässt, dass sich subjektiv die Grenze zur kontinuierlichen Einstellung vollends verwischen kann.

Vorteile und Grenzen der Anzeiger

Skalenanzeige	Ziffernanzeige
Anzeige
Bei analoger Messmethode ist die Anzeige in ihren Feinheiten nur schätzbar.	Bei digitaler Messmethode ist die Anzeige eindeutig ablesbar.
Die Auflösung ist begrenzt
durch die Ablesbarkeit auf 1/2 … 1/10 Skalenteilungswert ${\widehat {=}}$ 1 … 0,1 % vom Endwert.	durch die Stufung auf 1 Ziffernschritt (Digit) ≤0,1 % vom Endwert bei mindestens dreistelliger Anzeige.
Visuelle Betriebsüberwachung
ist auf einen Blick möglich.	erfordert bewusstes Lesen und Bewerten der Zahl.
Bei rascher Schwankung der Messgröße
(rasch im Verhältnis zur Einstell- oder Erfassungszeit)
ist eine mittlere Größe ablesbar.	ist der Anzeiger ungeeignet.
Trendbeobachtung oder Störerkennung
ist anhand Kurvenzug (mittels Schreiber oder Bildschirm) anschaulich leicht möglich.	ist anhand Zahlenkolonnen (mittels Drucker oder Bildschirm) mühsam.

Kodierung

Kodierung ist die Darstellung einer Nachricht in einer willkürlich gewählten Form. Je nach den Umständen sind verschiedene Kodierungen zweckmäßig.

Strichscheibe für inkrementelles Messen

Zählkode

Darstellung durch eine Folge von gleichwertigen Zeichen (Impulsen); bei jedem Impuls ist um einen Ziffernschritt weiterzuzählen.
Bei nicht elektrischen Messgrößen kann man Impulse durch optische Abtastung (z.B. an Strichscheibe) oder induktive Abtastung (z.B. an Zahnrad) erzeugen.

Gesamtzahl

Die Anzahl der Impulse repräsentiert die zu kodierende Zahl selber.

Beispiele:

Strichliste
Anzahl der Umdrehungen einer Welle oder, bei vielen Impulsen pro Umdrehung, ihre Positionierung.
Volumenmessung mit Ovalradzähler oder Turbinenradzähler.

Ovalradzähler: Mit jeder halben Umdrehung fließen oben und unten je ein „Volumenquant“ hindurch.

Zeitlich befristete Zählung

Die Zahl $\Delta N$ der Impulse in einer Zeitspanne $\Delta t$ repräsentiert die zu kodierende Zahl .

${\frac {\Delta N}{\Delta t}}=n\cdot z$

mit = Zuordnungsfaktor, z.B. Zahl der Impulse pro Umdrehung, wenn für die Drehzahl steht.

Beispiele:

Häufigkeits- bzw. Frequenzmessung
Drehzahlmessung
Durchflussmessung

Ein Frequenzsignal besitzt mit seiner Zählbarkeit wesentliche Vorteile eines Digitalsignals, obwohl die Frequenz wegen ihrer stetigen Veränderbarkeit eindeutig ein Analogsignal ist.

Ist die zu messende Größe als frequenz-proportionale Größe durch Zählung zu bestimmen, so muss die Dauer der Zählung begrenzt sein.

Die Zählung eignet sich für verschiedene Messaufgaben:

am Beispiel des Ovalradzählers:

Volumen-Messung für den Verkauf (Abgabemenge),
Durchfluss-Messung für den Betrieb (Förderleistung oder Strömungsgeschwindigkeit).

Je nach Aufgabe muss während der (im Ergebnis unwichtigen) Gesamtdauer der Verladung gezählt werden oder befristet nach Zeittakt.

am Beispiel von Induktionsschleifen in der Fahrbahn zum Fußballstadion:
- Unbefristete Zählung für die Auslastung des Parkplatzes,
- Befristete Zählung für die Leistungsfähigkeit der Straße.

Positionskode

Darstellung durch eine Folge von Zeichen, die je nach Position in einem Verbund unterschiedlich zu werten sind.

Dezimale Darstellung

Jede Ziffer hat die Stellenwertigkeit oder den Gewichtsfaktor einer Zehnerpotenz.

Beispiel: Dezimalzahl 145 = 5⋅10⁰ + 4⋅10¹ + 1⋅10²

Winkelkodierer mit 9 Binärstellen

Die Unterdarstellung der Dezimalziffern ist

mechanisch kein Problem, zum Beispiel bei
- Dekadenwiderständen,
- Ziffernrollen,
elektronisch schwierig.

Binäre oder duale Darstellung

Im einfachsten Fall, der auch häufig vorkommt, hat jede Ziffer die Stellenwertigkeit oder den Gewichtsfaktor einer Zweierpotenz.

Beispiel: Binärzahl/Dualzahl 10010001 = 2⁰ + 2⁴ + 2⁷ = 1 + 16₁₀ + 128₁₀ = 145₁₀

Bei nicht elektrischen Messgrößen kann man Binärziffern mittels Kodescheiben oder Kodelinealen darstellen, die so viele Bahnen besitzen, wie es Stellen gibt.

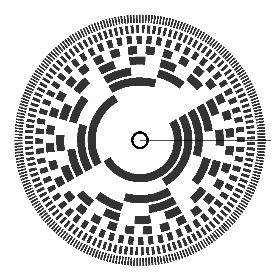
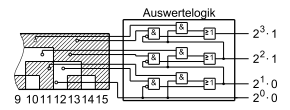
Beispiel: Winkelkodierer

Im Bild wird mit 9 Fühlern längs des gezeichneten Radius von innen nach außen die Binärzahl 111010101 ${\widehat {=}}$ 330° abgetastet, wenn hell ${\widehat {=}}$ 0 und dunkel ${\widehat {=}}$ 1 bewertet wird.

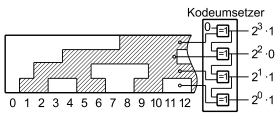
Vierspuriges Kodelineal mit Problem des Abtast-Fehlers

Durch Unvollkommenheit in der Justierung entstehen Fehler bei der Abtastung. Im gezeigten Beispiel eines Kodelineals wird zwischen 11 und 12 eine 8 gelesen, wenn unschraffiert ${\widehat {=}}$ 0 und schraffiert ${\widehat {=}}$ 1 bewertet wird. Dieser Fehler kann vermieden werden

durch Doppelabtastung,
durch Abtastung eines schmalen Synchronisationsfeldes in der Mitte des Feldes der feinsten Stufung,
durch Verwendung eines einschrittigen Kodes (im Bild Gray-Kode), in dem sich bei jedem Übergang $N\leftrightarrow N+1$ nur auf einer Spur ein Wert ändert; Nachteil: Keine Stellenwertigkeit auf den Spuren. Zu Auswertelogik und Kodeumsetzer siehe nachfolgend den Abschnitt "Bausteine der Binärtechnik".

Vermeidung des Abtastfehlers durch doppelte Abtastung

Vermeidung des Abtastfehlers durch einschrittigen Kode

Eine Auswahl möglicher Vier-Bit-Kodes

Bei intern binärer Darstellung ist zur Messwertanzeige an den beobachtenden Menschen eine Umkodierung auf eine Dezimalzahl erforderlich. Dazu muss das Gerät rechnen (dividieren) können, oder es verwendet die nachfolgende Mischform aus dezimal und binär.

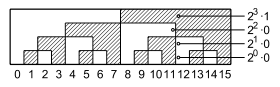
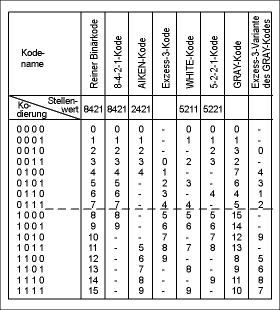
BCD-Darstellung

Mit einem BCD-Kode wird jede Dezimalstelle einzeln binär kodiert. Der Mindest-Aufwand beträgt 4 Binärziffern pro Dezimalziffer. Da von den 16 damit möglichen Bitkombinationen nur 10 gebraucht werden, gibt es mehrere gebräuchliche Kodes. Der 8-4-2-1-Kode hält die Stellenwertigkeit bei; andererseits vermeidet der Exzess-3-Kode die Kombinationen 0000 und 1111, die bei Fehlern besonders leicht auftreten können.

Beispiel im bevorzugten 8-4-2-1-Kode: 145₁₀ = 0001 0100 0101.

Bus-Ankopplung

In der Automatisierungstechnik gibt es eine Reihe von „-->Feldbussen“, z.B. Profibus, Interbus, EtherCAT, bei denen die Darstellung der Binärzeichen, der zeitliche Ablauf, der Aufbau eines Telegramms, die Datensicherung und manches mehr festgelegt werden. Darauf kann hier jedoch nicht eingegangen werden.

Gerätetechnik

Vorbemerkungen

Vorab wird ein Abschnitt der Elektronik eingeschoben. Er beschränkt sich auf das Notwendigste, um dem Verständnis der darauf folgenden Abschnitte zu dienen.

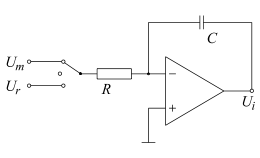
Operationsverstärker

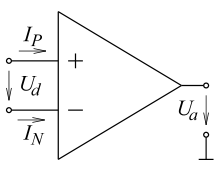
chaltzeichen des Operationsverstärkers; links zwei Eingänge, rechts ein Ausgang.
Hilfsanschlüsse, z.B. zur Speisung, werden im Allgemeinen nicht gezeigt

Der Operationsverstärker ist schlichtweg das Arbeitstier der Analog-Elektronik, da er je nach Beschaltung mit passiven Bauteilen für sehr vielfältige Aufgaben einsetzbar ist. Die entscheidende Formel zu seinem Verhalten lautet

$U_{a}=V_{0}\cdot U_{d}$

mit $V_{0}$ = Leerlauf-Spannungsverstärkung. Fast immer bestens zulässige Näherungen führen zum „idealen Operationsverstärker“:

$V_{0}\rightarrow \infty \quad ;\quad I_{P}\ ,\ I_{N}\rightarrow 0$

Anwendung ohne Rückkopplung als Komparator

Ohne Rückkopplung erfolgt keine Rückwirkung des Ausgangs auf den Eingang.

$U_{a}$ kann nur zwei Werte annehmen:

positiv übersteuert
negativ übersteuert.

Anwendung mit Rückkopplung auf den invertierenden Eingang

Strom-Spannungs-Umformer

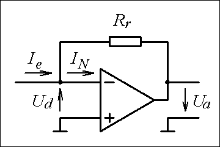
In der Zeichnung ist der invertierende Eingang mit Minuszeichen gekennzeichnet.

Die Schaltung kann ohne Übersteuerung analog-technisch betrieben werden. Dazu muss sich wegen $V_{0}\rightarrow \infty$ bei nicht übersteuertem Ausgang $U_{d}\rightarrow 0$ einstellen.

Strom-Spannungs-Umformer

Ein Strom-Spannungs-Umformer entsteht bei ohmscher Rückkopplung. Wegen $I_{N}=0$ fließt der gesamte Eingangsstrom $I_{e}$ durch den Rückkoppel-Widerstand. Bei einem positiven Eingangsstrom erzeugt der Verstärker eine negative Ausgangsspannung $U_{a}$ gerade so groß, dass $U_{d}=0$ wird. Damit gilt

$U_{a}=-\,I_{e}\cdot R_{r}\ .$

Integrator, Schaltung und Spannungs-Zeit-Diagramm für $U_{e}$ = konst > 0

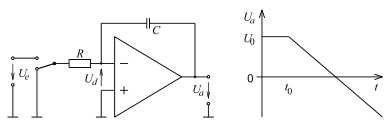
Integrator

Ein Integrator entsteht durch kapazitive Rückkopplung.

Wenn zum Zeitpunkt $t_{0}$ an den Eingang die Spannung $U_{e}$ geschaltet wird, und

wenn zum Zeitpunkt $t_{0}$ am Ausgang die Spannung $U_{a}=U_{0}$ anliegt,

dann ist für $t>t_{0}$

$U_{a}(t)=U_{0}-{\frac {1}{RC}}\int \limits _{t_{0}}^{t}U_{e}(t)\mathrm {d} t$

Falls $U_{e}$ = konst

$U_{a}(t)=U_{0}-{\frac {U_{e}}{RC}}(t-t_{0})$

Das ergibt eine Gerade mit dem Anstieg $-\,U_{e}/(RC)\,.$

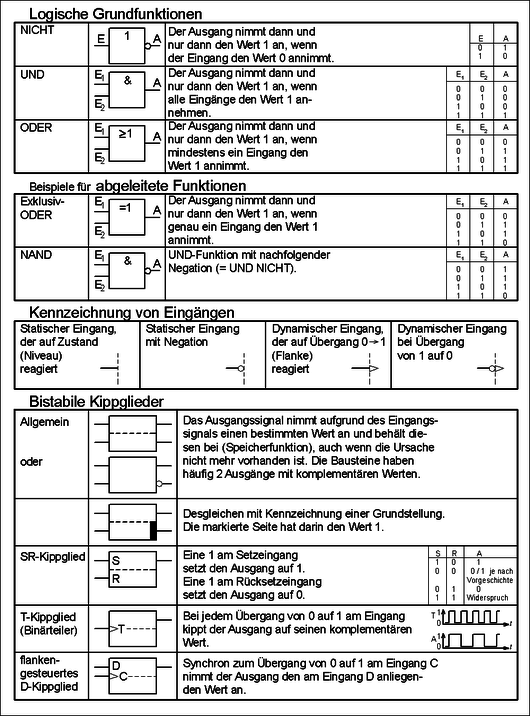
Bausteine der Binärtechnik

Siehe auch Logikgatter, Flipflop

Einige elementare Binärbausteine

Zähler

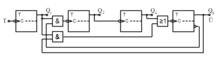
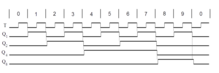
Zähler aus T-Kippgliedern für eine Dezimalstelle in BCD-Darstellung

Signal-Zeit-Verlauf zu vorstehender Schaltung (jedes Kippglied reagiert auf fallende Flanke)

Zähler arbeiten speichernd; sie haben eine Anzahl stabiler Zustände. Jeder Impuls bewirkt die Änderung des Speicherinhaltes um einen Ziffernschritt.

Zähler arbeiten bei befristeter Zählung mittelwertbildend über die Dauer der Zählung.

Mechanische Zähler haben Speicherglieder mit zehn stabilen Zuständen.
Elektronische Zähler haben Speicherglieder mit zwei stabilen Zuständen. In Dezimalzählern wird dazu ein Speicherglied aus vier Kippgliedern hergestellt.

Zur Zählung über mehrere Dezimalstellen kann der Übertragsausgang Ü im gezeigten Schaltplan mit dem Takteingang T einer weiteren Zählstufe für die nächsthöhere Stelle verbunden werden.

Zähleraufbau und Zusatzeinrichtungen

Zähler mit Zusatzeinrichtungen

Der gezeigte vierstellige Dezimalzähler hat ein paar Zusatzeinrichtungen:

Tor

Nur solange am unteren Eingang eine 1 anliegt, gelangen Zählimpulse auf den Zähler.

Rückstellung

Damit lässt sich der Zähler auf 0 setzen.

Vorwahl

Bei Übereinstimmung aller Dezimalstellen mit der Vorwahl-Einstellung wird eine Vorwahl-Meldung ausgegeben. Damit kann man weitere Ereignisse steuern, z.B.

Zählung beenden,
Zähler zurücksetzen und ab 0 weiterzählen.

Darüber hinaus gibt es Vor-/Rückwärtszähler. Diese enthalten einen weiteren Steuereingang für die Zählrichtung und erfordern eine Meldung über die Richtung einer Veränderung. Solche Zähler werden beispielsweise verwendet

bei der Positionsmessung mittels Inkrementalgeber, wenn beide Bewegungsrichtungen zulässig sind,
bei der Spannungsmessung mittels Nachlauf-Umsetzer bei steigender oder fallender Spannung.

Zähleranwendungen

An einer etwas anderen Schaltung reagieren der Zähleingang Z und der Start-Stopp-Eingang S auf den Übergang von 1 nach 0 des Eingangssignals. Vielfältige Anwendungen werden anhand der Tabelle erklärt. Danach folgen einige Ergänzungen.

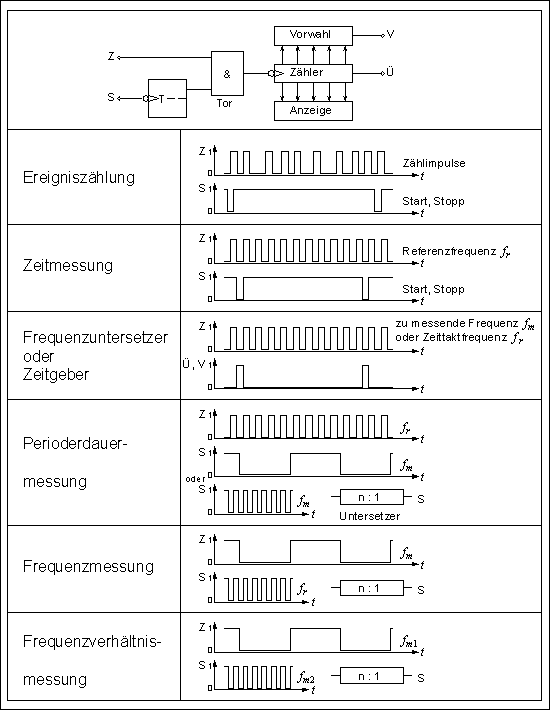
Verschiedene Messfunktionen und Hilfsfunktionen mittels Zähler

Zeitmessung

Beispiel mit der Annahme einer Referenzfrequenz $f_{r}$ = 1 kHz mit der Periodendauer $T_{r}$ = 1 ms:

Zwischen Start und Stopp seien Impulse gezählt worden. Dann sind zwischen Start und Stopp ms vergangen.

Frequenzuntersetzer

Frequenzuntersetzer für eine zu messende Frequenz $f_{m}$

Beispiel bei 5 Dezimalstellen:

Am Übertragsausgang Ü Untersetzung 100 000 : 1.

Beispiel bei an Vorwahlschaltern einstellbaren Zahl

und bei automatischer Rücksetzung:

Am Vorwahlausgang V Untersetzung

: 1.

Zeitgeber

Zeitgeber mittels Referenzfrequenz $f_{r}$ mit denselben Annahmen wie zuvor:

An Ü erscheint ein Impuls alle 100 s.

An V erscheint ein Impuls alle

ms.

Periodendauermessung

Falls die Messung auf einen zu kleinen Zählerstand führt, ist die Zähldauer zu verlängern mit einem Hilfszähler für $f_{m}$ .

Beispiel: Mit $f_{r}$ = 1 kHz und $f_{m}$ = 50 Hz ist der Zählerstand 20 ± 1,

mit Voruntersetzer für $f_{m}$ 1000 : 1 ist der Zählerstand 20 000 ± 1.

Hinweis: Ein Untersetzer 4000 : 1 mit Zähler-Ergebnis 80 000 ± 1 würde die relative Messunsicherheit weiter verkleinern, ist aber nicht angebracht. Die Umrechnung der Anzeige zum Messwert erfolgt üblicherweise nur in ganzen Zehnerpotenzen (keine numerische Rechnung, nur Kommaverschiebung);

im Beispiel: Zählerstand 20 000 ergibt $T_{m}$ = 20,000 ms.

Frequenzverhältnismessung

Anwendungsbeispiel: Kraftstoffverbrauchsmessung in Fahrzeugen

Die nicht unmittelbar messbare Größe $\Delta V/\Delta s$ (in l / 100 km) kann gebildet werden aus der Division
$\Delta V/\Delta t$ durch $\Delta s/\Delta t$ . Da beide Größen leicht durch frequenz-proportionale Signale dargestellt werden können,

$f_{m1}\sim {\frac {\Delta V}{\Delta t}}$ (Durchfluss) und $f_{m2}\sim {\frac {\Delta s}{\Delta t}}$ (Geschwindigkeit)

ist die Division durch Bildung des Frequenzverhältnisses möglich.

Universalzähler

Die Realisierung der in vorstehender Tabelle gezeigten Vielfalt ist in einem einzigen Gerät möglich. Dieses benötigt

Zähler für den anzuzeigenden Wert,
Zähler als Hilfsuntersetzer,
Präzisions-Frequenzgeber (Schwingquarz),
Schalter zu unterschiedlichen Kombinationen der Baugruppen.

Fehlergrenzen am Beispiel der Zeitmessung

Garantiefehlergrenzen

Quarze haben Abweichungen in ihrer Frequenz

typisch (selbst bei Konsumartikeln möglich) $\left|{\frac {\Delta f_{r}}{f_{r}}}\right|$ < 10⁻⁵,
mit höherem Aufwand (z.B. Thermostatisierung im Quarzofen) ist erreichbar < 10⁻⁸,
Atomuhr-Frequenzstandards (z.B. Rubidium-Oszillator) schaffen < 10⁻¹¹.

Bei Zählern über 5 Dekaden (also Zählerstand < 10⁵) mit Verwendung einer Quarzzeitbasis gilt durch diese typischen Fehlergrenzen der Referenzfrequenz $f_{r}$

$\left|{\frac {\Delta f_{r}}{f_{r}}}\right|=\left|{\frac {\Delta N}{N}}\right|<10^{-5}\quad ;\quad |\Delta N|<10^{-5}\cdot N<1\ .$

Der Aufwand bezüglich der Fehlergrenzen des Quarzes ist beim gegebenen Zähler optimal gewählt; es lohnt nicht, die Garantiefehlergrenzen unter einen Quantisierungsschritt zu drücken.

Messunsicherheit

Für die Messunsicherheit durch Zählung gilt am Beispiel einer zu messenden Zeit

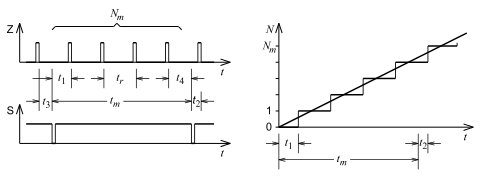
$t_{m}=N_{m}\cdot t_{r}-t_{3}+t_{4}=N_{m}\cdot t_{r}+t_{1}-t_{2}=t_{r}\cdot (N_{m}+\Delta N)\ .$

Zur Quantisierungs- bzw. Digitalisierungsabweichung bei der Zeitmessung

Die digital angezeigte Zeit unterscheidet sich von der richtigen Zeit um die Messabweichung

$F=t_{2}-t_{1}=t_{3}-t_{4}\ .$

Da diese Differenz positiv oder negativ sein kann, dem Betrage nach aber kleiner als $t_{r}$ bleibt, gilt die bekannte Tatsache

$\;-1<\Delta N<+1\ .$

Zeitmess-Abweichung bei Synchronisation

Gelingt es im Sonderfall,

den Taktgeber mit dem Beginn des auszumessenden Vorgangs zu synchronisieren oder
den Vorgang synchron mit dem Taktgeber zu starten,

so halbiert sich die Breite der möglichen Abweichung, und je nach Ausführung liegt diese zwischen

$\,0<\Delta N<+1$

und

$\,-1<\Delta N<0\ .$

Das sieht man im nächsten Bild mit schmalen Impulsen – je nachdem, ob die Schaltung auf fallende oder steigende Flanken reagiert.

Bei einer Frequenzuntersetzung aus einem fortlaufenden Takt gibt es Synchronisation sowohl am Anfang wie am Ende der erzeugten Periode, so dass das Frequenzverhältnis immer exakt ist.

Digital-Analog-Umsetzer (DAU)

DAU in der Messtechnik

Es gibt nur wenige physikalische Größen, bei denen eine Quantelung bekannt ist. Da selbst diese quantisierte Natur praktisch nicht erkennbar ist, besteht für einen DAU als Messgerät kein Bedarf. (Wer misst schon einen elektrischen Strom dadurch, dass Elektronen gezählt werden, außer bei unter 10⁻¹⁶ A?) Da der DAU aber Bestandteil mancher Messgeräte und einfach ein Gegenstück zum ADU ist, soll er hier behandelt werden.

Ein Digital-Analog-Umsetzer ist streng genommen etwas Widersinniges: Aus etwas Gestuftem lässt sich nicht etwas Stufenloses machen. Der DAU soll vielmehr so verstanden werden: Er setzt eine digital kodierte Information um in eine Form, die ein analog arbeitendes Gerät verstehen kann.

Repräsentative Ausführungen

Von den zahlreichen Entwicklungen werden hier drei erläutert.

DAU mit gewichteten Widerständen

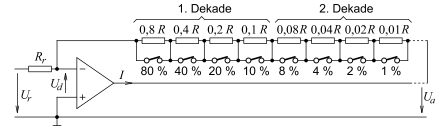
Schaltung zum DAU mit Spannungssummierung

Die Schaltung zeigt einen DAU mit Spannungssummierung durch gewichtete Widerstände in BCD-Darstellung. Hier entsteht die Spannung $U_{a}$ durch Vorgabe von zwei Dezimalziffern in 8-4-2-1-Kode sowie der Referenzspannung $U_{r}$ .

$U_{a}$ ist einstellbar durch Öffnen von Schaltern zwischen 0 und 99 % von $I\cdot R$ in einer Schrittweite von 1 %. Bei Bedarf für feinere Auflösung können weitere Dekaden angehängt werden, solange das von der Qualität der Widerstände und Schalter her zu verantworten ist. (Denn unerwünschte Eigenschaften von Schaltern und Widerständen beeinflussen mitunter die Ungenauigkeit der Ausgangsgröße.)

$I=-\,U_{r}/R_{r}\ ,$

wegen $U_{d}=0$ (virtuelle Masse); unabhängig von den Schalterstellungen.

Durch jede binäre Eins der binär kodierten -stelligen Dezimalzahl wird jeweils der zugehörige Schalter geöffnet und somit der betreffende Widerstand in die Kette der Widerstände eingeschleift.

$U_{a}=I\cdot \sum R_{\text{ein}}=-{\frac {\mathrm {Dezimalzahl} }{10^{n}}}\cdot U_{r}\cdot {\frac {R}{R_{r}}}\ .$

DAU mit Widerstandskettenleiter

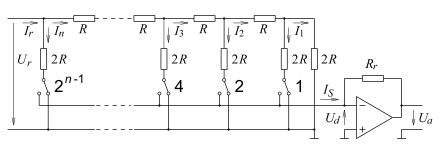
Schaltung zum DAU mit Stromsummierung

Die Schaltung zeigt einen DAU mit Stromsummierung durch Widerstandskettenleiter (R-2R-Netzwerk) in Binärdarstellung. Es gibt nur zwei Widerstandswerte unabhängig vom Stellenwert der jeweiligen Ziffer. Hier entsteht die Spannung $U_{a}$ durch Vorgabe von Binärziffern.

$I_{i}=2^{i-1}\cdot I_{1}$

für $i=1\,\ldots \,n$ .

$I_{r}=U_{r}/R=2\cdot I_{n}=2^{n}\cdot I_{1}$ .

Durch jede Eins der Binärzahl wird jeweils der zugehörige Schalter nach links gelegt, und der hindurch fließende Strom wird auf die Sammelleitung von $I_{S}$ geschaltet. Dieser Summenstrom fließt weiter durch den Rückkoppelwiderstand $R_{r}$ zum Ausgang des Operationsverstärkers.

$I_{S}=\sum _{i}I_{i\;{\text{ein}}}=I_{1}\cdot \mathrm {Bin{\ddot {a}}rzahl}$

$U_{a}=-I_{S}\cdot R_{r}=-{\frac {\mathrm {Bin{\ddot {a}}rzahl} }{\displaystyle 2^{n}}}\cdot U_{r}\cdot {\frac {R_{r}}{R}}\ .$

Allgemein: Für die beiden bisher gezeigten Ausführungen werden benötigt

Präzisions-Spannungsquelle,
Präzisionswiderstände,
Halbleiterschalter, die möglichst ideal sperren oder leiten.

DAU mit Pulsweitenmodulation

Schaltung zum DAU mit Pulsbreiten-Modulation

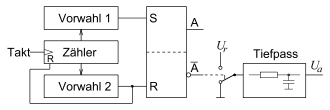
Die Schaltung zeigt einen DAU mit Pulsweitenmodulation. Hier entsteht die Spannung $U_{a}$ durch Vorgabe einer Zahl für den Tastgrad einer Rechteckspannung.

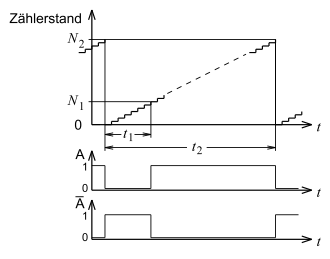
Zeitlicher Verlauf bei der Pulsbreiten-Modulation

Ein anfangs auf null gestellter Zähler erfasst eine Taktfrequenz $f_{r}$ und vergleicht seinen Zählerstand mit zwei vorgewählten Zahlen. Bei Erreichen der ersten Zahl $N_{1}$ (nach einer Zeit $t_{1}$ ) wird ein SR-Kippglied auf A = 1 gesetzt. Bei Erreichen der zweiten Zahl $N_{2}$ (nach einer Zeit $t_{2}$ ) wird das Kippglied auf A = 0 gesetzt, und auch der Zähler wird auf null zurückgestellt. Solange A = 0 ist, wird an einen Tiefpass oder Mittelwertbilder eine Referenzspannung $U_{r}$ gelegt, für den Rest der Periodendauer wird Null-Potential angelegt. Der arithmetische Mittelwert dieser Spannung ist

$U_{a}={\frac {t_{1}}{t_{2}}}U_{r}={\frac {N_{1}}{N_{2}}}U_{r}\ .$

Der Vorteil dieser Schaltung liegt im Verzicht auf Präzisionswiderstände und viele Schalter, der Nachteil liegt in ihrer langsamen Reaktion durch den Tiefpass.

Mit $N_{2}$ legt man die Feinheit der Stufung und die Periodendauer $t_{2}$ fest. Mit $N_{1}$ legt man die Spannung fest, wobei $U_{a}\sim N_{1}$ ist. Darf die kleinste Schrittweite 0,4 % vom Endwert betragen, so wählt man $N_{2}$ ≈ 250, wozu ein Zähler mit 8 Bit reicht. Bei $f_{r}$ = 1 MHz ist dafür $t_{2}$ = ¼ ms erforderlich. Mikroprozessor-Schaltungen bieten Zähler mit 16 Bit an; damit ist die Auflösung viel feiner möglich, aber dann ist im Maximalfall $t_{2}$ = 65 ms, und die Reaktionszeit liegt je nach Anforderung an die Glättung bei ≫ 200 ms.

Analog-Digital-Umsetzer (ADU)

Messgeräte für Prozessgrößen

Bereits in den vorhergehenden Abschnitten sind verschiedene Analog-Digital-Umsetzer behandelt worden zur

Frequenzmessung (Drehzahl-, Durchflussmessung)
Volumenmessung
Winkel- und Längenmessung
- inkrementales Verfahren mit Strichscheibe
- absolutes Verfahren mit Kodescheibe,
Zeitmessung.

Elektrische Spannungsmessgeräte

Ausführungsarten

Je nach Messaufgabe steht eine Vielzahl von Geräten nach folgenden Gesichtspunkten zur Auswahl:

Messwertausgabe
mit Rechneranschluss	mit Sichtanzeige
Messwertdarstellung und -auflösung
in reinem Binärkode mit 8 … 14 (… 28) Stellen	in BCD-Darstellung mit 2000 … 100 000 Punkten oder "3½-stellig" … 5-stellig (… 8½-)
Absolute Auflösung
kleinste auflösbare Spannung: Standardgeräte 100 μV Spitzengeräte 1 μV … 10 nV
Arbeitsweise
Schnell mit Momentanwert-Quantisierung – bei rasch veränderlichen Messgrößen oder wenn eine größere Anzahl von Messstellen über Umschalter (Multiplexer) abgefragt werden soll.	Langsam mit Mittelwertbildung (Integration) – zur Unterdrückung von Netzbrummen (netzsynchrone Stör-Wechselspannung) oder Störimpulsen (aus Schaltvorgängen).
Messdatenerfassung mit Multiplexer	Integration schwächt den Störeinfluss ab. Integration über ein ganzzahliges Vielfaches der Periodendauer des Störsignals unterdrückt ihn völlig; der in der Spannung enthaltene Gleichanteil oder Mittelwert ${\overline {U}}$ bleibt erhalten.

Schaltung zum Parallel-Umsetzer

Repräsentative Ausführungen

Von den zahlreichen Entwicklungen werden hier vier erläutert, zwei schnelle und zwei integrierende.

Parallel-Umsetzer

Die zu messende Spannung $U_{m}$ wird mit allen möglichen Quantisierungsstufen gleichzeitig verglichen. Zur Gewinnung einer -stelligen Binärzahl benötigt man $2^{n}-1$ Komparatoren.

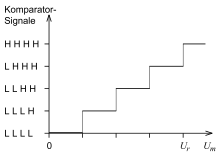
Kennlinie eines Parallelumsetzers. H steht für HIGH = positiv übersteuert, L für LOW = negativ übersteuert.

Zur Funktionsweise am Beispiel mit n=2 :

Es werden vier vom Spannungsteiler gebildete Spannungen $U_{r}$ , ${\frac {3}{4}}U_{r}$ , ${\frac {1}{2}}U_{r}$ , ${\frac {1}{4}}U_{r}$ gleichzeitig mit $U_{m}$ verglichen. Dieser aus Gründen der Übersichtlichkeit sehr grob gestufte Umsetzer kann nur 4 verschiedene Messwerte liefern. Der vierte Komparator für die höchste Stufe der Kennlinie liefert einen fünften Wert: Überschreitung des Messbereichs.

Parallel-Umsetzer sind extrem schnell („flash-converter“) und extrem aufwändig. Ausführungen mit ≥ 6 Bits arbeiten in der Spitzenklasse bei einer Umsetzzeit ≤ 1 ns (Umsetzrate ≥ 1 GHz). Auch sind integrierte Umsetzer mit 10 Bits (1023 Komparatoren) auf dem Markt.

Eine Weiterentwicklung sind die Pipeline-Umsetzer. Sie sind aus mehreren selbständigen Stufen in Pipeline-Architektur aufgebaut. Ihre Stufen bestehen in der Regel aus Parallel-Umsetzern über wenige Bits. In jeder Pipelinestufe wird eine grobe Quantisierung vorgenommen, dieser Wert wieder mit einem DAU in ein analoges Signal umgesetzt und vom zwischengespeicherten Eingangssignal abgezogen. Der Restwert wird verstärkt und der nächsten Stufe zugeführt. Die Vorteile liegen in der stark verminderten Anzahl an Komparatoren (60 für vier Vier-Bit-Umsetzerstufen) und in der höher möglichen Auflösung bis 16 Bit. Mit jeder Stufe erhöht sich die Latenzzeit, aber die Abtastrate vermindert sich nur wegen der bei höherer Auflösung längeren Einschwingdauer.

Serieller Umsetzer

Schaltung zum seriellen Umsetzer

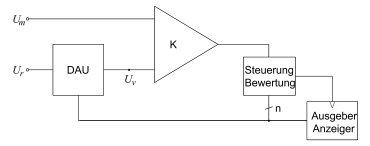
Die zu messende Spannung $U_{m}$ wird mit einer am DAU erzeugten Spannung $U_{v}$ verglichen. Nacheinander wird $U_{v}$ in mehreren Schritten verändert und an $U_{m}$ möglichst genau angenähert. Dazu gibt es mehrere Strategien; hier wird die sukzessive Approximation mit dem Wäge- oder Kompensationsverfahren erklärt.

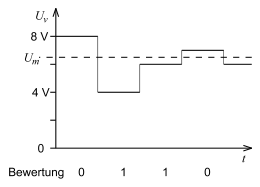
Zeitlicher Verlauf bei der sukzessiven Approximation (zum Beispiel laut Text)

Zur Funktionsweise

Annahme:	$U_{m}$ > 0 und $U_{v}$ > 0
Schritt 1a:	Es wird eine Vergleichsspannung $U_{v}$ erzeugt, indem das höchstwertige Bit auf 1 gesetzt wird und alle anderen auf 0.
Schritt 1b:	Wenn $U_{v}>U_{m}$ , dann wird das Bit auf 0 zurückgesetzt. Wenn $U_{v}<U_{m}$ , dann wird das Bit auf 1 gelassen.
Schritt 2a:	Eine 1 auf dem nächst niederwertigeren Bit wird hinzugefügt.
Schritt 2b:	Wie Schritt 1b
u. s. w.

Zur Gewinnung einer -stelligen Binärzahl benötigt man Vergleiche. Zum Schluss ist $U_{m}-U_{v}<U_{q}$ . Dabei ist $U_{q}$ der kleinste am DAU einstellbare Spannungssprung.

Beispiel hierzu:

4-Bit-DAU mit $U_{q}$ = 1 V bei $U_{m}$ = 6,5 V.

Gemäß Signal-Zeit-Diagramm erhält man den Messwert = 0110_B ⋅ $U_{q}$ = 6 V.

Das zum Schluss eingestellte Eingangssignal des DAU wird als Ergebnis des ADU angesehen (binär oder BCD gestuft).

Messung von Augenblickswerten; $U_{m}$ darf sich allerdings während der Einstellung von $U_{v}$ nicht ändern. Dazu wird oft eine Sample-and-Hold-Schaltung verwendet, die $U_{m}$ während der Umsetzung analog zwischenspeichert. Typische Umsetzdauer 1 … 100 μs.

ADU mit der Zwischengröße Zeit

Schaltung zum Zweirampen-Verfahren

Das Verfahren wird am Zweirampen- oder Dual-Slope-Verfahren erklärt.

Die zu messende Spannung $U_{m}$ lädt für eine begrenzte Dauer den Kondensator eines Integrators (siehe oben im Abschnitt Operationsverstärker). Danach wird der Kondensator wieder kontrolliert entladen. Beide Vorgänge laufen bei Gleichspannung aufgetragen über der Zeit rampenförmig (linear) ab.

Zur Funktionsweise

Annahme:	$U_{m}>0$ ; dann $U_{r}<0$
Beginn:	bei mit $U_{i}=0$
Schritt 1:	Aufintegration (Aufladung des Kondensators) mit $U_{m}$ für eine feste Dauer, z.B. $t_{i}$ = 20 ms. $U_{i}(t_{i})=-{\frac {1}{RC}}\int \limits _{0}^{t_{i}}U_{m}\mathrm {d} t=-{\frac {t_{i}}{RC}}U_{m\;{\text{gemit}}}$
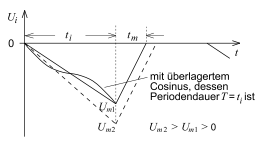
Schritt 2:	Abintegration mit $U_{r}$ auf festen Endwert $U_{i}=0$ . $U_{i}(t_{i}+t_{m})=0$ $=-{\frac {t_{i}}{RC}}\ U_{m\;{\text{gemit}}}-{\frac {1}{RC}}\int \limits _{t_{i}}^{t_{i}+t_{m}}U_{r}\mathrm {d} t$ ${\frac {t_{i}}{RC}}U_{m\;{\text{gemit}}}=-{\frac {1}{RC}}U_{r}\cdot t_{m}$ $U_{m\;{\text{gemit}}}=-U_{r}{\frac {t_{m}}{t_{i}}}\;;\ U_{m\;{\text{gemit}}}\sim t_{m}$ (Zwischengröße)

Zeitlicher Verlauf beim Zweirampen-Verfahren

Beide Zeiten werden durch Zählung bestimmt. Angezeigt wird

$N_{m}=f_{r}\cdot t_{m}\quad$ .

Für die Aufintegrations-Dauer verwendet wird

$N_{i}=f_{r}\cdot t_{i}\quad$ .

$U_{m\ {\text{gemit}}}=-U_{r}{\frac {N_{m}}{N_{i}}}\ ,$ unabhängig von $R{\text{, }}C{\text{, }}f_{r}$ .

$N_{m}$ steht für den über die Dauer der Aufintegration gemittelten Wert der zu messenden Spannung; wirksame Störunterdrückung von 50-Hz-Signalen, wenn $t_{i}={\frac {k}{50\;\mathrm {Hz} }}=k\cdot 20\;\mathrm {ms}$ ; mit k>0 , ganzzahlig. Dann ist $U_{m\ {\text{gemit}}}={\overline {U_{m}}}\ .$

Typische Integrationsdauer 1 … 300 ms. Geräte mit $t_{i}=k\cdot {\text{ 100 ms}}$ bieten gute Unterdrückung von Netz-Einkopplung weltweit, sowohl bei 50-Hz- als auch bei 60-Hz-Netzen.

ADU mit der Zwischengröße Häufigkeit

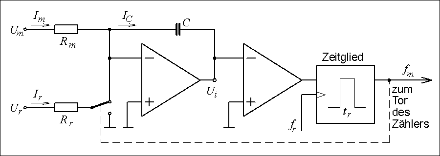
Schaltung zum Ladungsbilanz-Verfahren

Das Verfahren wird am Ladungsbilanz- oder Charge-Balancing-Verfahren erklärt.

Die zu messende Spannung $U_{m}$ lädt in einem Integrator den Kondensator. Durch kurze Stromstöße in Gegenrichtung wird er ständig wieder entladen; im Mittel ist die Ladungsbilanz ausgeglichen.

Zur Funktionsweise

Zeitlicher Verlauf beim Ladungsbilanz-Verfahren

Annahme:	$U_{m}>0$ ; dann $U_{r}<0$
ferner:	$-I_{r}$ > 2 ⋅ Maximalwert von $I_{m}$
Beginn:	bei mit $U_{i}=0$
Schritt 1:	Laden mit $I_{m}+I_{r}<0$ für feste kurze Dauer $t_{r}$ , wobei $t_{r}=1/f_{r}$ ≪ 20 ms
Schritt 2:	Entladen mit $I_{m}>0$ auf festen Endwert $U_{i}=0$
Schritt 3:	wie Schritt 1
u. s. w.

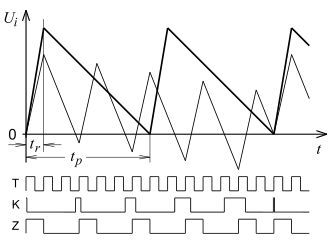
Das Signal-Zeit-Diagramm zeigt im oberen Teil die Spannung $U_{i}$ am Ausgang des Integrators bei einer zu messenden Gleichspannung $U_{m}$ . Längs der dickeren Sägezahn-Linie ist nach einer Periode jeweils die Ladungsbilanz ausgeglichen.

$\int \limits _{0}^{t_{p}}I_{C}\mathrm {d} t=0=t_{r}\cdot (I_{m}+I_{r})+(t_{p}-t_{r})\cdot I_{m}$

$I_{m}=-I_{r}{\frac {t_{r}}{t_{p}}}{\text{ ;}}\quad I_{m}\sim {\frac {1}{t_{p}}}=f_{m}$ (Zwischengröße)

Die Messung von $f_{m}$ führt durch Zählung für die Dauer $t_{i}$ auf den Zählerstand $N_{m}$ , der angezeigt wird.

Als Zeitgeber für $t_{i}$ wird die Frequenz $f_{r}$ gezählt bis zum Zählerstand $N_{i}$ ; $t_{i}=N_{i}\cdot t_{r}$

Zur Größenordnung: $t_{i}$ = einige 100 ms.

Die im Bild dünnere Sägezahnlinie unterscheidet sich von der dickeren in zwei Punkten:

Die Spannung $U_{m}$ ist um den Faktor 5/2 größer und erzeugt eine um denselben Faktor größere Zahl von Ladezyklen.
Die Meldung des Komparators startet das Zeitglied nicht sofort.

In der hier gezeigten Schaltung erzeugt das Zeitglied die Dauer $t_{r}$ präzise von einer steigenden Flanke von $f_{r}$ bis zur nächsten. Durch diese Synchronisation des Zeitgliedes an die Taktfrequenz läuft $U_{i}$ nicht nur bis zur Nulllinie, sondern weiter bis zum Zeitpunkt der Synchronisation. Die damit verbundene Abweichung macht aber weniger als einen Ziffernschritt aus – über eine beliebig lange Zähldauer. Die drei Rechtecksignale im Bild erläutern den Vorgang zum Verlauf der dünneren Linie von $U_{i}$

oberes Signal für den Takt (also $f_{r}$ ),
mittleres Signal für den Ausgang des Komparators,
unteres Signal für den Ausgang des Zeitgliedes.

In der Zähldauer $t_{i}$ fließt der Strom $I_{m}$ ständig. Zusätzlich wird $N_{m}$ mal kurzzeitig der Strom $I_{r}$ eingeschaltet, so dass der Kondensator sich im Mittel nicht auflädt.

$\int \limits _{0}^{t_{i}}I_{C}\mathrm {d} t=0=\int \limits _{0}^{t_{i}}I_{m}\mathrm {d} t+I_{r}\cdot t_{r}\cdot N_{m}$ $;\quad I_{m\;{\text{gemit}}}\cdot t_{i}=-I_{r}\cdot t_{r}\cdot N_{m}$

$U_{m\;{\text{gemit}}}=R_{m}I_{m\;{\text{gemit}}}=-R_{m}I_{r}{\frac {N_{m}}{N_{i}}}=-U_{r}{\frac {R_{m}}{R_{r}}}{\frac {N_{m}}{N_{i}}}\ ,$ nur abhängig von der Referenzspannung und einem Widerstandsverhältnis, unabhängig von $C{\text{ und }}f_{r}$ .

In seiner messtechnischen Qualität ist dieses Verfahren mit dem Zweirampenverfahren ähnlich, aber diesem noch etwas überlegen ( $U_{m}$ ist ununterbrochen eingeschaltet).

Messabweichungen

Für Messabweichungen, die allein durch die Unvollkommenheit des digitalen Spannungsmessgerätes bedingt sind, werden in der Regel vom Hersteller Fehlergrenzen angegeben. Diese setzen sich aus zwei Anteilen zusammen,

aus der Vergleichsgröße resultierend (und eventuell weiteren multiplikativ ins Ergebnis eingehenden Ursachen) und
aus Nullpunkt und Digitalisierung resultierend (und eventuell weiteren additiv eingehende Ursachen).

Störspannungen bei digitalen Multimetern

Beispiele zur korrekten Angabe und Verwendung siehe unter Messgeräteabweichung und Digitalmultimeter.

Als wichtige Einflussgrößen, die Messabweichungen hervorrufen können und die in den Geräte-Fehlergrenzen nicht enthalten sind, kommen infrage

Stromaufnahme der Eingangsklemmen,

sowie bedingt durch die Eigenschaften der angelegten Spannung

Frequenz,
Kurvenform,
überlagerte Störspannung,
- Serienstörspannung, die bei integrierenden Verfahren unterdrückbar ist z.B. um den Faktor 10⁻³ bei 50 und 60 Hz,
- Gleichtaktstörspannung, die bei integrierenden Verfahren unterdrückbar ist z.B. um den Faktor 10⁻⁵ bei 0 … 10 kHz.

Anmerkung

Grundlage des Artikels ist das zweibändige Werk
F. Dokter und J. Steinhauer: Digitale Elektronik in der Meßtechnik und Datenverarbeitung.
Band I: Theoretische Grundlagen und Schaltungstechnik. 1969
Band II: Anwendung der digitalen Grundschaltungen und Gerätetechnik. 3. Auflage, 1973
Philips Fachbücher, Hamburg.

Basierend auf einem Artikel in:

Wikipedia.de