Thermoelektrizität

Unter Thermoelektrizität versteht man die gegenseitige Beeinflussung von Temperatur und Elektrizität und ihre Umsetzung ineinander. Seebeck-Effekt (auch thermoelektrischer Effekt), Peltier-Effekt und Thomson-Effekt beschreiben jeweils eine umkehrbare Wechselwirkung zwischen den beiden physikalischen Größen.

Effekte

Seebeck-Effekt

Eine einfache Schaltung, an der sich der Seebeck-Effekt zeigt. An den Punkten T₁ und T₂ treffen sich die Materialien A und B des elektrischen Leiters.

Am Widerstand liegt eine, durch den Seebeck-Effekt erzeugte, elektrische Spannung an. Dadurch fließt durch den Widerstand ein elektrischer Strom.

Gemäß dem Seebeck-Effekt, benannt nach Thomas Johann Seebeck, entsteht in einem Stromkreis aus zwei verschiedenen elektrischen Leitern bei einer Temperaturdifferenz zwischen den Kontaktstellen eine elektrische Spannung der Größe

$U = \int_{T_1}^{T_2} \left( S_\mathrm{B}(T) - S_\mathrm{A}(T) \right) \, \mathrm{d}T.$

Dabei sind T_2 und T_1 die Temperaturen der Kontakte zwischen den Materialien A und B. Die Seebeck-Koeffizienten $S_\mathrm{A}$ und $S_\mathrm{B}$ sind Materialkonstanten, die auch von der Temperatur abhängen. Alternativ wird als Symbol auch ein $\alpha$ benutzt. Der Seebeck-Koeffizient hat die Dimension einer elektrischen Spannung pro Temperaturdifferenz (Volt/Kelvin). Die typische Größenordnung liegt für Metalle bei Raumtemperatur bei 10 µV/K.

Für kleine Temperaturdifferenzen und konstante Werte für die Seebeck-Koeffizienten vereinfacht sich die Formel zu

$U = (S_\mathrm{B} - S_\mathrm{A}) \cdot (T_2 - T_1)$

In der Thermospannung tritt immer nur die Differenz der Seebeck-Koeffizienten auf. Da sich einzelne (absolute) Seebeck-Koeffizienten nur schwer bestimmen lassen (siehe Thomson-Effekt), wurde Platin als Referenzelement für tabellierte Zahlenwerte gewählt.

Der Seebeck-Effekt beschreibt ausschließlich die Entstehung dieser Spannung. Ein durch äußere Beschaltung entstehender Stromfluss ist nicht Teil dieses Effektes und folgt lediglich aus dem Ohmschen Gesetz.

Historisches

Thomas Johann Seebeck entdeckte zufällig, dass in einem Stromkreis aus zwei unterschiedlichen Metallen (z.B. in Stangenform) eine elektrische Spannung entsteht, wenn zwischen den zwei Verbindungsstellen der Stangen ein Temperaturunterschied herrscht. Dass dabei elektrischer Strom fließt, konnte er über das dabei auftretende Magnetfeld mit Hilfe der dafür typischen Ablenkungen einer in ihm platzierten Kompassnadel nachweisen. Seebeck nutzte diesen Effekt 1821 in einem ersten Thermoelement aus.

Erklärung

Die Spannung entsteht durch Thermodiffusionsströme in einem Material. Die Betrachtung nur eines Materials mit Temperaturgradienten liefert also eine hinreichende Erklärung. Für Messzwecke braucht man zwei verschiedene Metalle. Am heißen Ende des Leiters gibt es mehr Elektronen mit hoher Energie und weniger Elektronen mit geringer Energie (unterhalb des chemischen Potenzials). Durch Diffusion bewegen sich entsprechend energiereiche Elektronen zum kalten Ende und Elektronen mit wenig Energie in die entgegengesetzte Richtung. Dies beschreibt die Wärmeleitung durch Elektronen. Ein eventuelles Ungleichgewicht der Ströme wird durch ein elektrisches Feld ausgeglichen, da im offenen Stromkreis kein Strom fließen kann. Die entstehende Spannung (Integral des elektrischen Feldes) ist die Seebeck-Spannung.

Sie wird durch die Abhängigkeit der Beweglichkeit und Zahl (Zustandsdichte) der Elektronen von der Energie bestimmt. Die Abhängigkeit der Beweglichkeit von der Energie hängt empfindlich von der Art der Streuung der Elektronen ab. Entsprechend können auch relativ kleine Verunreinigungen die Thermokraft recht stark beeinflussen. Die treibende Kraft für die Diffusion ist proportional zur Temperaturdifferenz. Als groben Trend erwartet man daher für Metalle eine Zunahme der Seebeck-Koeffizienten etwa proportional zur Temperatur.

Ein Spezialfall ist der so genannte Elektronen-Drag. Bei niedrigen Temperaturen von etwa 1/5 der Debye-Temperatur werden die Phononen vor allem durch Stöße mit Elektronen gebremst. Die Phononen ziehen dabei die Elektronen mit in Richtung niedriger Temperaturen. Dadurch können in diesem Temperaturbereich die thermoelektrischen Effekte etwas größer werden, als man es sonst erwartet. Bei höheren Temperaturen gewinnen Umklappprozesse für die Streuung der Phononen an Bedeutung und der Effekt wird kleiner.

Zahlenwerte

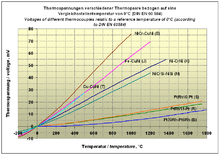
Thermospannungen gebräuchlicher Thermopaare

Seebeckkoeffizienten einiger Metalle und Legierungen relativ zu Platin:

Werkstoff	α in µV/K bei 273 K
Bismut	−72
Konstantan	−35
Nickel	−15
Platin	−00
Kohlenstoff	−03
Aluminium	−03,5
Rhodium	−06
Kupfer	−06,5
Gold	−06,5
Silber	−06,5
Eisen	−19
Nichrome	−25

Um den absoluten Seebeckkoeffizienten der hier angegebenen Materialien zu erhalten, muss der absolute Seebeckkoeffizient von Platin (zwischen −4,04 µV/K bei 273 K und ca. −5 µV/K bei 300 K) addiert werden.

Peltier-Effekt

Ein Peltier-Element mit Halbleitern (N und P) versorgt von einer Batterie

Beim Peltier-Effekt, angewandt bei dem Peltier-Element, liegen gegenüber dem Seebeck-Effekt umgekehrte Verhältnisse vor – ein elektrischer Stromfluss bewirkt eine Änderung des Wärmetransportes. Während jedoch der Seebeck-Effekt das Entstehen einer Spannung beschreibt, tritt der Peltier-Effekt ausschließlich durch das Fließen eines elektrischen Stromes auf. In einem stromdurchflossenen Thermopaar treten immer beide Effekte auf, bei metallischen Thermopaaren ist der Peltier-Effekt jedoch nur schwer nachweisbar. Die Entdeckung machte Jean Peltier daher erst 1834, dreizehn Jahre nach der Entdeckung des Seebeck-Effektes.

Wenn ein elektrischer Strom I an einen Kontakt von einem Material A in ein Material B fließt, entsteht eine Wärmequelle der Größe:

$\dot{Q} = \Pi_\mathrm{AB} I = \left(\Pi_\mathrm{A} - \Pi_\mathrm{B} \right) I$

Die Peltierkoeffizienten $\Pi_\mathrm{B}, \Pi_\mathrm{A}$ sind dabei Materialkonstanten, die im Allgemeinen von der Temperatur abhängen.

Je nach Vorzeichen des Stromes kann dabei Wärme freigesetzt oder Wärme entzogen werden. In aller Regel wird also der eine Kontakt warm und der andere kalt.

Erklärung

Zur Erklärung des Peltiereffekts genügt die Verknüpfung mit dem Seebeck-Effekt über die Thomson-Relationen. Es gibt für den Peltiereffekt aber auch eine relativ anschauliche direkte Erklärung: Bewegte Elektronen transportieren neben der Ladung e auch immer Energie. Wie viel das im Mittel ist, hängt unter anderem davon ab, wie die Zahl der Ladungsträger und die Streurate von der Energie abhängen. Höherenergetische Elektronen tragen stärker zum Strom bei, transportieren gleichzeitig aber auch mehr Energie. Beim Übergang von einem Material zum anderen ändert sich die mit den Elektronen transportierte Energie. Die Differenz wird an der Kontaktstelle als Wärme freigesetzt oder aufgenommen (Peltier-Effekt). Die mit dem Elektron transportierte Energie entspricht dabei gerade dem Peltierkoeffizienten. In Halbleitern ist der Abstand zwischen chemischem Potential und der Bandkante dabei ein wesentlicher Anteil. Insbesondere kann so erklärt werden, dass in Halbleitern die thermoelektrischen Effekte oft wesentlich größer sind als in Metallen.

Thomson-Effekt

(nicht zu verwechseln mit dem Joule-Thomson-Effekt oder dem Gibbs-Thomson-Effekt oder dem Thomson-Effekt als Galvanomagnetischem Effekt)

Der Thomson-Effekt, benannt nach William Thomson, 1. Baron Kelvin 1856, beschreibt den geänderten Wärmetransport entlang eines stromdurchflossenen Leiters, in welchem ein Temperaturgradient vorliegt.

Jeder stromdurchflossene Leiter mit einer Temperaturdifferenz zwischen zwei Punkten wird, abhängig vom Metall, entweder mehr oder weniger Wärme transportieren, als dies ohne Stromfluss aufgrund der Wärmeleitfähigkeit der Fall wäre. Dieser Effekt überlagert sich jedoch mit der Erwärmung des elektrischen Leiters durch den Strom auf Grund seines Widerstandes und ist daher schlecht nachweisbar.

Eine Stromdichte in einem homogenen Leiter verursacht eine Wärmeleistung pro Volumeneinheit von

$q = \rho J^2 - \mu J \frac{\mathrm{d}T}{\mathrm{d}x}$

wobei $\rho$ der spezifische Widerstand des Materials, $\mathrm{d}T/\mathrm{d}x$ der Temperaturgradient im Leiter und $\mu$ der Thomson-Koeffizient sind.

Der erste Ausdruck $\rho J^2$ ist die irreversible Joulesche Erwärmung. Der zweite Term ist die Thomson-Wärme, deren Vorzeichen mit der Richtung des Stromes wechselt.

Für den Thomson-Effekt gibt es noch keine technische Anwendung. Über den Thomson-Effekt lassen sich durch Integration über die Temperatur die absoluten thermoelektrischen Koeffizienten bestimmen.

Thomson-Relationen

Seebeck-, Peltier- und Thomson-Effekt sind nicht unabhängig voneinander, sondern haben eine gemeinsame Ursache. Schon 1854 fand Thomson zwischen den entsprechenden Koeffizienten zwei Zusammenhänge, die Thomson-Relationen (gelegentlich auch Kelvin-Relationen) genannt werden:

$\Pi = S \cdot T$

$\mu = T \cdot \mathrm{d}S/\mathrm{d}T$

Dabei sind

$\Pi$ der Peltier-Koeffizient
S der Seebeck-Koeffizient
T die absolute Temperatur
$\mu$ der Thomson-Koeffizient.

Die zweite Gleichung sagte den Thomson-Effekt voraus.

Anisotrope Materialien

Im allgemeinen Fall eines anisotropen Materials können die elektrische und thermische Leitfähigkeit Tensorgrößen sein. Entsprechendes gilt dann auch für die thermoelektrischen Koeffizienten. So ist es damit z.B. möglich, dass Wärme freigesetzt wird, wenn der Strom an einer Korngrenze die Richtung relativ zu den Kristallachsen ändert. Dies wird Bridgman-Effekt genannt, nach dem amerikanischen Physiker P. W. Bridgman.

In aller Regel wird die Richtungsabhängigkeit vernachlässigt. Viele Materialien sind schon wegen kubischer Symmetrie tatsächlich isotrop hinsichtlich der Leitfähigkeit.

Anwendungen und Auswirkungen

Thermoelemente aus Metallen wandeln thermische Energie nur sehr ineffizient in elektrische Energie um und werden daher fast nur als Thermoelement zur Temperaturmessung eingesetzt. Zur Messung kleiner Temperaturdifferenzen können viele Thermoelemente elektrisch in Reihe geschaltet werden, z.B. in der Thermosäule zur Messung von Strahlung.

Die Thermospannungen treten als störender Effekt bei der Messung kleiner Gleichspannungen auf. Hier muss entsprechend auf kleine Temperaturgradienten und eine passende Materialwahl geachtet werden.

Durch Einsatz von Halbleitermaterialien (Werkstoffe und Aufbau siehe bei Peltier-Element) lässt sich der Umwandlungswirkungsgrad auf bis zu 3–8 % steigern und liegt damit deutlich unter dem Carnot-Wirkungsgrad. Damit kann man thermoelektrische Generatoren bauen. Solche Generatoren bzw. Wandler finden u.a. in Isotopenbatterien Anwendung und wandeln verschleißfrei ohne bewegte Teile Wärmeenergie in elektrische Energie um.

Der Peltier-Effekt lässt sich in Peltier-Elementen zur Kühlung und Temperaturregelung nutzen. Wegen des relativ schlechten Wirkungsgrades bleibt dies aber auf eher kleine Anwendungen beschränkt. Vorteilhaft sind dabei die gute Skalierbarkeit, Regelbarkeit und Zuverlässigkeit. Vom Aufbau und den geforderten Materialeigenschaften sind Peltier-Elemente und thermoelektrische Generatoren ähnlich.

Die technische Anwendung zur Kühlung ist durch die phononische Wärmeleitung begrenzt, sie bewirkt insbesondere bei großen Temperaturdifferenzen einen entgegengerichteten Wärmestrom, der etwa ab 70 K den durch den Stromfluss hervorgerufenen Wärmestrom aufhebt. Aus dem gleichen Grund haben thermoelektrische Generatoren nur einen geringen Wirkungsgrad.

Für den Thomson-Effekt gibt es keine technische Anwendung. Der Effekt ist so klein, dass schon der praktische Nachweis schwierig ist.

Neuere Entwicklungen

Die Wirkungsgrade von Peltier- und Seebeck-Elementen sind trotz aller Forschungsprogramme niedrig geblieben. Der schlechte Wirkungsgrad kommt durch die ungewollte Wärmeleitung zwischen den Metallen bzw. Halbleitern zustande. Ein neuerer Ansatz, diese zu unterbinden, verfolgt das Thermotunneling-Verfahren: Zwei Metalle werden durch einen minimalen luftleeren Spalt voneinander getrennt. Die Wärmeleitung über Gitterschwingungen wird so vollständig unterbunden. Der Vakuum-Spalt ist jedoch nur so breit, dass ihn einzelne Elektronen quantenmechanisch „tunneln“ können.

Auf den ersten Blick scheint diese Unterbrechung der phononischen Wärmeleitung, d.h. die Wärmeleitung über Gitterschwingungen, äußerst effizient zu sein. Bei einer Spaltgröße, welche ein quantenmechanisches Tunneln ermöglicht, sind die elektromagnetischen Kräfte jedoch derart groß, dass eine nahezu ungehinderte Weiterleitung der Gitterschwingungen aufgrund von elektromagnetischer Kopplung stattfindet.

Eine effiziente Entkopplung der Gitterschwingungen findet erst dann statt, wenn die Spaltgröße im Bereich der Wellenlängen liegt. Bei üblichen Temperaturen, bei denen solche Elemente eingesetzt werden sollen, liegen die Wellenlängen der elektromagnetischen Emissionen im Bereich von einigen hundert Nanometern bis hin zu wenigen Mikrometern. Bei diesen Größen ist ein quantenmechanisches Tunneln jedoch praktisch nicht mehr möglich.

Siehe auch

Pyroelektrizität – ein anderes Verfahren zur Gewinnung von Elektrizität aus Temperaturunterschieden

Literatur

Thermospannungen – Viel genutzt und fast immer falsch erklärt! In: Physik und Didaktik in Schule und Hochschule, 1/4, 2005, S. 10–22.

Basierend auf einem Artikel in:

Wikipedia.de