Franck-Condon-Prinzip

Das Franck-Condon-Prinzip ist eine quantenmechanische Gesetzmäßigkeit, mit deren Hilfe sich Aussagen über die Wahrscheinlichkeiten von Übergängen zwischen verschiedenen Schwingungszuständen eines Moleküls machen lassen. Das Prinzip bezieht sich dabei auf den Fall, dass sich neben dem Schwingungszustand auch die elektronische Anregung des Moleküls ändert, und wird beispielsweise in der Molekularphysik, Spektroskopie und als aktives Medium von Moleküllasern (wie Farbstoff- und Molekülgaslaser) angewandt. Es ist nach den Physikern James Franck und Edward Condon benannt.

Physikalischer Hintergrund

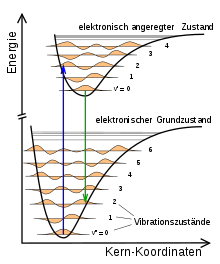
Abbildung 1: Schwarze Kurven: Energie eines zweiatomigen Moleküls in Abhängigkeit vom theoretisch festgehaltenen Abstand der Kerne, für zwei verschiedene Zustände der Elektronenhülle (schematisch). Die Schwingungszustände sind mit ihren Wellenfunktionen für den Kernabstand auf der Höhe der jeweiligen Energie eingezeichnet. Die beiden Pfeile stellen vibronische Übergänge dar.

Der innere Zustand eines Moleküls kann laut der Quantenmechanik nur bestimmte, diskrete Energiewerte annehmen. Ein Zustand wird dabei beschrieben durch eine Wellenfunktion. Bei einem Molekül kann eine Anregung des inneren Zustands, also eine Erhöhung der Energie bei ruhendem Massenmittelpunkt, auf drei Arten stattfinden:

elektronische Anregung (durch verschiedene Anregungszustände der Elektronen im Molekül),
Vibrations-Anregung (durch Molekülschwingungen, d.h. Schwingungen der Atomkerne des Moleküls gegeneinander),
Rotations-Anregung (durch die Rotation des Moleküls; diese spielt für das Franck-Condon-Prinzip nur eine untergeordnete Rolle).

In Abbildung 1 ist schematisch für zwei verschiedene elektronische Zustände eines zweiatomigen Moleküls die Energie in Abhängigkeit vom theoretisch festgehaltenen Abstand der Kerne dargestellt. Diese Energie wirkt sich bei den Kernen aus wie eine potentielle Energie und ermöglicht Schwingungszustände verschiedener Energie und Amplitude und wird daher als Potentialkurve bezeichnet. Beide sind mit Schwingungen der Kerne kombiniert, deren Wellenfunktionen auf der Höhe der jeweiligen Energie eingezeichnet sind. Abgebildet sind unten der elektronische Grundzustand und oben ein elektronisch angeregter Zustand, jeder von verschiedenen Vibrationszuständen des Moleküls begleitet, die mit den Zahlen bzw. v'' durchnummeriert werden. Die beiden senkrechten Pfeile stellen zwei vibronische Übergänge dar, wobei nach der Born-Oppenheimer-Näherung angenommen wird, dass der Kernabstand gleich bleibt. Solche vibronischen Übergänge können durch Absorption und Emission oder auch durch Stöße des Moleküls mit Elektronen, Atomen oder anderen Molekülen stattfinden.

Aussage

Das Franck-Condon-Prinzip beruht auf der Tatsache, dass der Wechsel von Elektronen zwischen verschiedenen Zuständen so schnell stattfindet (in ca. 10⁻¹⁵ Sekunden), dass sich der Abstand der Atomkerne zueinander während der Anregung nicht ändert (eine Kernschwingungsperiode dauert ca. 10⁻¹³ s.). Diese hohe Geschwindigkeit des elektronischen Übergangs gegenüber der Kernbewegung wird durch die geringe Masse der Elektronen ermöglicht (analog zur Born-Oppenheimer-Näherung).

Wenn ein Molekül nun von einem elektronischen Zustand in einen anderen übergeht, so ist dieser Übergang umso wahrscheinlicher, je mehr die Vibrations-Wellenfunktionen der beiden Zustände zueinander kompatibel sind (z.B. beim gleichen Kernabstand ein Maximum haben). Einige vibronische Übergänge sind damit wahrscheinlicher als andere, und zwar die, bei denen sich der Kernabstand nicht ändert. Für diese Übergänge wird ein senkrechter Pfeil (siehe Abbildung 1) gezeichnet, weshalb auch von „senkrechten Übergängen“ gesprochen wird.^[1] Mit dem durch das Franck-Condon-Prinzip gegebenen Formalismus lassen sich die Intensitäten dieser Übergänge berechnen, wie sie etwa für die Spektroskopie genutzt werden.

Am Beispiel der Zustände in Abbildung 1 bedeutet dies: Vom Vibrations-Grundzustand ( v''=0 ) im elektronischen Grundzustand ist der wahrscheinlichste Übergang in den elektronisch angeregten Zustand derjenige, der im Vibrations-Zustand v'=2 endet. Übergänge in andere Vibrations-Zustände können auch stattfinden, allerdings ist die Wahrscheinlichkeit dafür geringer.

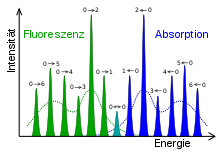
Abbildung 2: Schematische Darstellung der Intensitätsverteilung von vibronischen Übergängen gemäß dem Franck-Condon-Prinzip. Die Zahlen $v''\rightarrow v'$ geben dabei den Anfangszustand und Endzustand der Vibration an.

Ein Beispiel für eine solche Intensitätsverteilung zeigt Abbildung 2. Vibronische Übergänge vom elektronischen Grundzustand in den angeregten Zustand (Absorption) sind blau, die umgekehrten Übergänge (Fluoreszenz) dagegen in grün dargestellt. Die schmalen Linien werden beobachtet, wenn die Moleküle in Gasform vorliegen. Die gestrichelten Linien zeigen dagegen den Fall, dass die Moleküle in flüssiger oder fester Phase vorliegen: hier findet eine sogenannte Linienverbreiterung statt.

Quantenmechanische Formulierung

Der Anfangszustand des Übergangs setzt sich aus einem elektronischen Anteil (ε) und einem Vibrationsanteil (v) zusammen und sei in der Bra-Ket-Notation mit $\left|\psi\right\rangle$ bezeichnet. Für eine exakte Behandlung müsste zusätzlich noch der Spin berücksichtigt werden, der hier allerdings aus Gründen der Übersicht vernachlässigt wird, ferner der Rotationsanteil, der aber oft nur vernachlässigbare Zusatzenergien verursacht. Der Endzustand sei analog mit $\left|\psi '\right\rangle$ bezeichnet. Eine quantenmechanische Beschreibung außerhalb der Bra-Ket-Notation lässt sich ebenfalls in der Literatur finden.^[2]

Ein Übergang zwischen beiden Zuständen wird beschrieben durch den Dipoloperator ${\boldsymbol {\mu }}$ , der sich aus der Elementarladung −e und den Orten ${\boldsymbol {r}}_{{\mathrm {i}}}$ der Elektronen, sowie den Ladungen eZ_j und Orten ${\boldsymbol {R}}_{{\mathrm {j}}}$ der Atomkerne zusammensetzt:

${\boldsymbol {\mu }}={\boldsymbol {\mu }}_{\epsilon }+{\boldsymbol {\mu }}_{K}=-e\sum \limits _{i}{{\boldsymbol {r}}_{i}}+e\sum \limits _{j}{Z_{j}{\boldsymbol {R}}_{j}}$

Die Übergangswahrscheinlichkeit von $\left|\psi\right\rangle$ zu $\left|\psi '\right\rangle$ ist gegeben durch das Skalarprodukt

$P=\left\langle \psi '\right|{\boldsymbol {\mu }}\left|\psi \right\rangle$ ,

während die Intensität I des Übergangs das Quadrat dieser Übergangswahrscheinlichkeit ist:

$I=\left|P\right|^{2}$ .

Um diese zu berechnen wird ausgenutzt, dass die Wellenfunktion näherungsweise durch ein Produkt aus elektronischer und Vibrationswellenfunktion ausgedrückt werden kann:

$\psi \ =\psi _{\epsilon }({\boldsymbol {r}}_{i})\psi _{v}({\boldsymbol {R}}_{j})$ ,

wobei die elektronische Wellenfunktion $\psi _{\epsilon }$ allein von den Koordinaten der Elektronen abhängt und die Vibrationswellenfunktion $\psi _{v}$ allein von denen der Kerne.

Diese Separation der Wellenfunktionen ist analog zu der Born-Oppenheimer-Näherung zu verstehen. Sie ist die fundamentale Annahme bei der Ableitung des Franck-Condon-Prinzips. Zusammengefasst ergibt sich eine Gleichung für die Berechnung der Intensitäten:

${\begin{aligned}P&=\left\langle \psi _{\epsilon }'\psi _{v}'\right|{\boldsymbol {\mu }}\left|\psi _{\epsilon }\psi _{v}\right\rangle \\&=\left\langle \psi _{\epsilon }'\psi _{v}'\right|{\boldsymbol {\mu }}_{\epsilon }+{\boldsymbol {\mu }}_{K}\left|\psi _{\epsilon }\psi _{v}\right\rangle \\&=\left\langle \psi _{\epsilon }'\psi _{v}'\right|{\boldsymbol {\mu }}_{\epsilon }\left|\psi _{\epsilon }\psi _{v}\right\rangle +\left\langle \psi _{\epsilon }'\psi _{v}'\right|{\boldsymbol {\mu }}_{K}\left|\psi _{\epsilon }\psi _{v}\right\rangle \\&=\underbrace {\left\langle \psi _{v}'|\psi _{v}\right\rangle } _{\mathrm {{\ddot {U}}berlappungsintegral} \ }\cdot \underbrace {\left\langle \psi _{\epsilon }'|{\boldsymbol {\mu }}_{\epsilon }|\psi _{\epsilon }\right\rangle } _{\mathrm {{\ddot {U}}bergangsdipolmoment} }+\underbrace {\left\langle \psi _{\epsilon }'|\psi _{\epsilon }\right\rangle } _{=\,0}\left\langle \psi _{v}'|{\boldsymbol {\mu }}_{K}|\psi _{v}\right\rangle \\\end{aligned}}$

Hier wurde eine Vereinfachung vorgenommen, nämlich

$\left\langle \psi _{\epsilon }'\psi _{v}'\right|{\boldsymbol {\mu }}_{\epsilon }\left|\psi _{\epsilon }\psi _{v}\right\rangle \approx \left\langle \psi _{v}'|\psi _{v}\right\rangle \left\langle \psi _{\epsilon }'|{\boldsymbol {\mu }}_{\epsilon }|\psi _{\epsilon }\right\rangle$ ,

die nur zulässig ist, solange das über die Elektronen-Koordinaten gehende Skalarprodukt $\left\langle \psi _{\epsilon }'|{\boldsymbol {\mu }}_{\epsilon }|\psi _{\epsilon }\right\rangle$ wirklich unabhängig ist von der Position der Kerne. Dies ist in der Realität zwar nicht exakt der Fall, aber oft eine hinreichend gute Näherung. Der zweite Summand in oben gezeigter Gleichung verschwindet, da die Elektronen-Wellenfunktionen verschiedener elektronischer Zustände zueinander orthogonal sind.

Übrig bleibt ein Produkt aus zwei Termen: Das Quadrat des ersten Terms (Überlappungsintegral) ist der Franck-Condon-Faktor, während der zweite Term das Übergangsdipolmoment angibt, das durch die Bahndrehimpuls- und Spin-Auswahlregel für elektrische Dipolstrahlung bestimmt wird.^[3]^[4]

Das Überlappungsintegral hängt ausschließlich von den Kernkoordinaten ab. Es zeigt die Überlappung zwischen den vibratorischen Wellenfunktionen der am Übergang beteiligten elektronischen Zustände (Grund- und Anregungszustand).^[5] Hieraus folgt, dass vibronische Übergänge intensiver sind, je besser die Schwingungswellenfunktionen überlappen. Dies zeigt sich in der Größe der Franck-Condon-Faktoren, die im Bereich von $S=1$ (maximale Überlappung) bis $S=0$ (keinerlei Überlappung) reicht.^[6]

Das Franck-Condon-Prinzip macht Aussagen über erlaubte vibronische Übergänge zwischen zwei verschiedenen elektronischen Zuständen, wobei weitere quantenmechanische Auswahlregeln die Wahrscheinlichkeiten dieser Übergänge modifizieren oder diese gar ganz verbieten können. So gilt die Schwingungsauswahlregel $\Delta v=\pm 1$ hier nicht mehr, da es sich um Schwingungswellenfunktionen unterschiedlicher elektronischer Zustände handelt.^[7] Die Schwingungsauswahlregel wird vielmehr quasi durch die Franck-Condon-Faktoren ersetzt. Auswahlregeln in Bezug auf die Rotation des Moleküls wurden hier vernachlässigt. Sie spielen in Gasen eine Rolle, während sie in Flüssigkeiten und Festkörpern vernachlässigbar sind.

Hervorzuheben ist, dass die quantenmechanische Formulierung des Franck-Condon-Prinzips das Ergebnis einer Reihe von Annäherungen ist, vor allem der Dipol-Näherung sowie der Born-Oppenheimer-Näherung. Die mit ihrer Hilfe berechenbaren Intensitäten können in der Realität abweichen, beispielsweise dann, wenn zusätzlich magnetische Dipolübergänge oder elektrische Quadrupolübergänge berücksichtigt werden müssen oder die beschriebene Faktorisierung in einen elektronischen sowie Vibrations- und Spin-Anteil nicht hinreichend zulässig ist.

Literatur

Originale Veröffentlichungen von Franck und Condon in Fachzeitschriften:

J. Franck: Elementary processes of photochemical reactions. In: Trans. Faraday Soc. Nr. 21, 1926, S. 536–542, doi: 10.1039/TF9262100536.
E. U. Condon: A Theory of Intensity Distribution in Band Systems. In: Phys. Rev. Nr. 28, 1926, S. 1182–1201, doi: 10.1103/PhysRev.28.1182.
E. U. Condon: Nuclear Motions Associated with Electron Transitions in Diatomic Molecules. In: Phys. Rev. Nr. 32, 1928, S. 858–872, doi: 10.1103/PhysRev.32.858.

Lehrbücher zum Thema:

Peter W. Atkins, Ronald S. Friedman: Molecular Quantum Mechanics. 4. Auflage. Oxford University Press, 2004, ISBN 0-19-927498-3.
Gerhard Herzberg: Molecular Spectra and Molecular Structure. 2. Auflage. Krieger Publishing Company, 1992, ISBN 0-89464-789-X.

Einzelnachweise

↑ J. Michael Hollas: Moderne Methoden in der Spektroskopie. Vieweg, Braunschweig/Wiesbaden 1995, ISBN 3-528-06600-8, S. 226–230.
↑ Karl Hensen: Molekülbau und Spektren. Steinkopff, Darmstadt 1973, ISBN 978-3-7985-0607-7, S. 127–130.
↑ David J. Willock: Molecular Symmetry. Wiley, Chichester 2009, ISBN 978-0-470-85348-1, S. 339–342.
↑ Daniel C. Harris, Michael D. Bertolucci: Symmetry and Spectroscopy. Dover, New York 1978, ISBN 0-486-66144-X, S. 330–332.
↑ Robert L. Brooks: The Fundamentals of Atomic and Molecular Physics. Springer, New York/Heidelberg 2013, ISBN 978-1-4614-6677-2, S. 151.
↑ P. Atkins, J. de Paula: Physical Chemistry. Freeman, New York 2006, ISBN 0-7167-8759-8 S. 486.
↑ Gerd Wedler: Lehrbuch der Physikalischen Chemie. Wiley-VCH, Weinheim 2004, ISBN 978-3-527-31066-1, S. 621.

Basierend auf einem Artikel in:

Wikipedia.de