Numerische Apertur

Die numerische Apertur (Formelzeichen $A_{\text{N}}$ , NA oder n.A., von lateinisch apertus, dt. offen) ist eine dimensionslose Größe, die das Vermögen eines optischen Elements beschreibt, Licht zu fokussieren. Der Begriff wurde vom Physiker Ernst Abbe eingeführt.

Bei einem Objektiv bestimmt die numerische Apertur die minimale Größe des Lichtflecks, der in seinem Fokus erzeugt werden kann; eine große numerische Apertur ist gut für das Auflösungsvermögen.

Mathematische Beschreibung und Zusammenhang mit dem Auflösungsvermögen

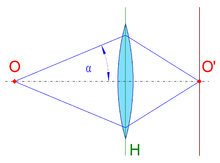
Der halbe objektseitige Öffnungswinkel α für die Bestimmung der numerischen Apertur bei der optischen Abbildung eines Objektpunktes O nach O' mit Brechung der Randstrahlen an der Hauptebene H einer Feldlinse

Die numerische Apertur $A_{\text{N}}$ ergibt sich aus dem Produkt des Sinus des halben objektseitigen Öffnungswinkels (Akzeptanzwinkel) $\alpha$ und dem Brechungsindex n des Materials zwischen Objektiv und Fokus (siehe auch Immersion (Mikroskopie)):

$A_{\text{N}}=n\cdot \sin \alpha$

Ein optisches Element, z.B. ein Objektiv, wird charakterisiert durch seine Vergrößerung, seine numerische Apertur, den optischen Arbeitsabstand und den rückwärtigen Abbildungsabstand.

Mathematisch richtig wird der Öffnungswinkel durch eine Blende in der hinteren Brennebene des Objektivs bestimmt. Bautechnisch ist aber die Fassung der ersten Linse limitierend; dies ist näherungsweise auch richtig, wie im Rahmen der Fraunhofer-Beugung erläutert wird.

Die maximale Auflösung ist der minimale Abstand zwischen zwei unterscheidbaren Strukturen $d_{\rm {min}}$ . In der Mikroskopie ist die Größe des Fokus durch Beugung begrenzt und proportional zur Wellenlänge $\lambda$ des verwendeten Lichtes sowie umgekehrt proportional zur numerischen Apertur:

$d_{\text{min}}={\frac {1{,}22\cdot \lambda }{2\cdot A_{\text{N}}}}={\frac {0{,}61\cdot \lambda }{A_{\text{N}}}}$

Als Faustformel ergibt sich folgende Beziehung zur Abschätzung der maximalen Auflösung:

$d_{\text{min}}\approx {\frac {\lambda }{A_{\text{N}}}}$

Im Vakuum oder in Luft und großem Öffnungswinkel ( $n\approx 1\rightarrow A_{\text{N}}\lesssim 1$ ) ergibt sich als Abschätzung:

$d_{\text{min}}\approx \lambda$

Vergrößerung der numerischen Apertur

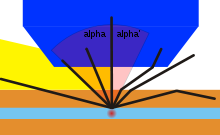
Numerische Apertur beim Mikroskop: $\alpha '$ in Luft und $\alpha$ für ein Medium mit

In Luft mit n=1 (z.B. bei einem Fernrohr) ist die numerische Apertur immer kleiner als eins. Sie kann aber Werte größer als eins annehmen, wenn der Raum zwischen zu mikroskopierender Probe und Mikroskop-Objektiv mit einer Immersionsflüssigkeit gefüllt wird, deren Brechungsindex größer ist als eins; häufig wird Wasser ( $n=1{,}33$ ), Glycerin ( $n=1{,}47$ ) oder Öl ( $n=1{,}51$ ) benutzt. Bei Mikroskopen steigt die numerische Apertur in der Regel mit der Vergrößerungszahl des Objektivs, die starkvergrößernden Objektive (90x, 100x, bei hochauflösenden Objektiven auch 40x und 60x) brauchen dementsprechend Immersionsflüssigkeit zwischen Objektiv und Objekt (Deckglas).

Praktische Zusammenhänge

Auch bei Lichtwellenleitern wird die numerische Apertur beschrieben durch den Sinus des Akzeptanzwinkels (manchmal auch Kollimations-/Divergenzwinkel) der Faser und entspricht der Öffnung des kegelförmigen Lichtbündels, das aus der Endfläche der Faser wieder austritt.

Bei optischen Abbildungen sind häufig andere Effekte wie Aberrationen oder andere Abbildungsfehler so groß, dass das über die numerische Apertur berechenbare theoretisch mögliche Auflösungsvermögen nicht erreicht werden kann. Als Kompromiss wird hierbei häufig die kritische Blende eingestellt, bei der bei einem vorgegebenen Objektiv in der Praxis das größte Auflösungsvermögen erreicht werden kann.

Ähnlich ist es in der Fotografie, wo anstelle der numerischen Apertur häufig das Öffnungsverhältnis angegeben wird. Dieses bezieht sich jedoch – anders als die numerische Apertur – auf den bildseitigen Öffnungswinkel (siehe Öffnungsverhältnis und Blendenzahl).

Die Auflösung kann über die Beugungsgrenze hinaus erhöht werden durch Ausnutzen nichtlinearer Reaktionen der Moleküle, z.B. bei den Analysemethoden STORM, dSTORM, STED oder (f)PALM.

Literatur

Ernst Leitz: Mikroskope. Verlag Leitz, 1897, Kapitel Numerische Apertur, S. 10.
Ernst Abbe: Die Lehre von der Bildentstehung im Mikroskop. bearbeitet von Otto Lummer und Fritz Reiche, Verlag Vieweg, 1910.

Basierend auf einem Artikel in:

Wikipedia.de