Öffnungswinkel
Als Öffnungswinkel
einer Sammellinse oder eines Objektivs (allgemein
eines fokalen
optischen Systems)
wird der Winkel bezeichnet, den ein Punkt auf der optischen Achse
mit dem Durchmesser der Eintritts-
bzw. Austrittspupille
bildet.
Konkret unterscheidet man:
- objektseitiger Öffnungswinkel
, definiert als der Winkel zwischen dem Objektpunkt auf der optischen Achse und dem Durchmesser der Eintrittspupille:
- bildseitiger Öffnungswinkel
, definiert als der Winkel zwischen dem Bildpunkt auf der optischen Achse und dem Durchmesser der Austrittspupille:
-
- Er bestimmt die Größe der Zerstreuungskreise und beeinflusst somit die Abbildungstiefe.
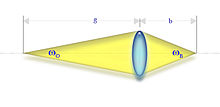
Öffnungswinkel einer Sammellinse
Bei Fotoobjektiven entsprechen die Positionen der Eintritts- bzw. Austrittspupille in der Regel nicht mehr der Lage der Hauptebenen, auch ist ihr Durchmesser üblicherweise variabel. Außerdem enthalten Objektive zusätzliche Blenden und sind meistens aus mehreren Linsen aufgebaut.
Dagegen fallen bei einer Sammellinse
Eintritts- und Austrittspupille in der Linsenmitte zusammen – der Durchmesser
der Pupillen entspricht jeweils demjenigen der Linse. Somit entspricht der
Abstand des Objektpunktes zur Eintrittspupille der Gegenstandsweite ,
und der Abstand des Bildpunktes zur Austrittspupille entspricht der Bildweite
.
Dadurch vereinfachen sich die Verhältnisse so, dass sich die Öffnungswinkel bei einer Sammellinse berechnen lassen als:
- objektseitiger Öffnungswinkel
- bildseitiger Öffnungswinkel
Große Gegenstandsweite
Eine weitere Vereinfachung ergibt sich, wenn man den Öffnungswinkel bei sehr großen Gegenstandsweiten („unendlich“) betrachtet. Wächst die Gegenstandsweite über alle Grenzen, so wird
Gemäß der Linsengleichung entspricht die Bildweite bei unendlich großer Gegenstandsweite der Brennweite f, also wird
Öffnungsverhältnis und Blendenzahl
Für große Gegenstandsweiten g ergibt sich aus dem bildseitigen
Öffnungswinkel
und der Brennweite f eines optischen Systems das Öffnungsverhältnis 1/k:
Die Blendenzahl ist der Kehrwert des Öffnungsverhältnisses, also:
Die Eintrittspupille ist das Bild der Blende, welches man durch die Vorderseite des Objektivs sieht. So kann man auch Durchmesser schätzen.
Numerische Apertur
Aus dem objektseitigen Öffnungswinkel
und dem Brechungsindex n
des Mediums
ergibt sich die numerische
Apertur
:
Der Brechungsindex n der Luft ist etwa 1 (1,000292 in Bodennähe).
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 19.01. 2024