Transportsatz

Transportsätze oder Transport-Theoreme beschreiben die Regeln für die Zeitableitung von Integralen mit zeitabhängigen Integrationsgrenzen. Solche Zeitableitungen kommen in der Kontinuums- und Strömungsmechanik vor, wo die Integrale beispielsweise eine Zirkulation, einen Volumenstrom durch eine Fläche oder den Impuls einer sich bewegenden und deformierenden Masse darstellen. Das Integrationsgebiet kann entsprechend eine Linie, eine Fläche oder ein Volumen sein. Der Transportsatz für Volumen wird Reynolds’scher Transportsatz oder Reynolds-Transport-Theorem (nach Osborne Reynolds) genannt. Die Transportsätze werden verwendet, um grundlegende Erhaltungssätze der Kontinuumsmechanik herzuleiten. Mathematisch gesehen handelt es sich um Verallgemeinerungen der Leibnizregel für Parameterintegrale.

Alle betrachteten Felder müssen sowohl nach der Zeit als auch nach dem Ort einmal stetig differenzierbar und im betrachteten Gebiet integrierbar sein. Unstetigkeitsstellen in Form von nach dem Ort stetig differenzierbaren Flächen, an denen sich beispielsweise die Dichte sprunghaft ändert, können jedoch berücksichtigt werden. Bei der Herleitung der Transportsätze werden die Integrationsgrenzen zeitunabhängig dargestellt, der Integrand zeitlich abgeleitet und das Integrationsgebiet wieder in die zeitabhängige Form zurückgebracht.

Linien-, Flächen- und Volumenelemente für von der Masse transportierte Gebiete

Wenn die Gebiete sich mit der Masse mitbewegen, sie also materielle Grenzen aufweisen, dann kann die örtliche Differenzierbarkeit der Bewegungsfunktion der Masse ausgenutzt werden. Die substantielle Ableitung der Linien-, Flächen- und Volumenelemente sind dann gemäß der folgenden Tabelle gegeben.

Linienelement	${\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} {\vec {x}}=\operatorname {grad} ({\vec {v}})\cdot \,\mathrm {d} {\vec {x}}$
Vektorielles Oberflächenelement	${\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} {\vec {a}}=[\operatorname {div} ({\vec {v}})\mathbf {I} -\operatorname {grad} ({\vec {v}})^{\top }]\cdot \,\mathrm {d} {\vec {a}}$
Volumenelement	${\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} V=\operatorname {div} ({\vec {v}})\,\mathrm {d} V$

Der Operator $\tfrac{\mathrm{D}}{\mathrm{D}t}$ oder ein Hochpunkt wie in ${\dot f}$ bezeichnet die substantielle Zeitableitung, ${\vec {v}}({\vec {x}},t)$ das vom Ort ${\vec {x}}$ und der Zeit t abhängige Geschwindigkeitsfeld der Masse, grad den Gradienten und div die Divergenz eines Vektorfeldes, I den Einheitstensor und das hochgestellte T die Transposition.

Wenn sich das Integrationsgebiet relativ zur Masse bewegt, dann können die oben angegebenen Linien- und Oberflächenelemente nicht berechnet werden, weil in den Gebieten die für die Gradienten- und Divergenzbildung benötigte Umgebung fehlt. Statt auf die Lagrangesche Betrachtungsweise der Integrale zurückzugreifen, die materielle Integrationsgrenzen zeitunabhängig zu definieren gestattet, wird das Gebiet mit Parametern aus einem festen Intervall – hier [0,1]ⁿ, n=1,2,3 je nach Dimension n des Gebietes – beschrieben. Auch diese festen Grenzen erlauben es, die Zeitableitung in den Integranden zu verschieben.

Transportsatz für Linienintegrale

Gegeben sei eine sich durch die Masse bewegende Kurve b mit vektoriellem Linienelement $\mathrm {d} {\vec {b}}\,.$ Für die Kurve liege zu jeder Zeit t eine Parameterdarstellung ${\vec {b}}(\xi ,t)$ für die Punkte auf der Kurve mit Kurvenparameter ξ im Intervall [0,1] vor. Für das Linienelement gilt dann: $\mathrm {d} {\vec {b}}={\tfrac {\partial }{\partial \xi }}{\vec {b}}(\xi ,t)\,\mathrm {d} \xi \,.$ Die Zeitableitung des Kurvenintegrals einer vom Ort ${\vec {x}}$ und der Zeit t abhängigen Feldgröße ${\vec {f}}({\vec {x}},t)$ über den Weg b lautet dann:^[1]

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{b}{\vec {f}}({\vec {b}},t)\cdot \,\mathrm {d} {\vec {b}}=&{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{0}^{1}{\vec {f}}({\vec {b}}(\xi ,t),t)\cdot {\frac {\partial }{\partial \xi }}{\vec {b}}(\xi ,t)\,\mathrm {d} \xi =\int _{0}^{1}\left[\left({\frac {\partial {\vec {f}}}{\partial {\vec {x}}}}\cdot {\frac {\partial {\vec {b}}}{\partial t}}\right)\cdot {\frac {\partial {\vec {b}}}{\partial \xi }}+{\frac {\partial {\vec {f}}}{\partial t}}\cdot {\frac {\partial {\vec {b}}}{\partial \xi }}+{\vec {f}}\cdot {\frac {\partial ^{2}{\vec {b}}}{\partial \xi \partial t}}\right]\,\mathrm {d} \xi \\=&\int _{b}\left[{\frac {\partial {\vec {f}}}{\partial t}}+\operatorname {grad} ({\vec {f}})\cdot {\vec {v}}_{b}\right]\cdot \,\mathrm {d} {\vec {b}}+\int _{0}^{1}{\vec {f}}\cdot {\frac {\partial }{\partial \xi }}{\vec {v}}_{b}(\xi ,t)\,\mathrm {d} \xi \,.\end{aligned}}$

Für ein Skalarfeld gilt entsprechend:

${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{b}f({\vec {b}},t)\,\mathrm {d} {\vec {b}}=\int _{b}\left[{\frac {\partial f}{\partial t}}+\operatorname {grad} (f)\cdot {\vec {v}}_{b}\right]\,\mathrm {d} {\vec {b}}+\int _{0}^{1}f{\frac {\partial }{\partial \xi }}{\vec {v}}_{b}(\xi ,t)\,\mathrm {d} \xi \,.$

Wenn die Geschwindigkeit der Kurve ${\vec {v}}_{b}$ gleich der Geschwindigkeit ${\vec {v}}$ der Masse ist, dann steht in der eckigen Klammer die substantielle Zeitableitung der Feldgröße und die Ableitung der Geschwindigkeit in Richtung der Kurve kann mit dem Geschwindigkeitsgradient berechnet werden:^[1]

${\frac {\partial {\vec {v}}_{b}(\xi ,t)}{\partial \xi }}\,\mathrm {d} \xi ={\frac {\partial {\vec {v}}({\vec {b}}(\xi ,t),t)}{\partial \xi }}\,\mathrm {d} \xi ={\frac {\partial {\vec {v}}({\vec {x}},t)}{\partial {\vec {x}}}}\cdot {\frac {\partial {\vec {b}}(\xi ,t)}{\partial \xi }}\,\mathrm {d} \xi =\operatorname {grad} ({\vec {v}})\cdot \,\mathrm {d} {\vec {b}}={\frac {\mathrm {D} }{\mathrm {D} t}}\mathrm {d} {\vec {b}}({\vec {x}},t)\,.$

Dann geht dieser Transportsatz in den für von der Masse transportierte Linien aus der Tabelle über.

Skalarfeld	${\frac {\mathrm {D} }{\mathrm {D} t}}\oint _{b}f\,\mathrm {d} {\vec {b}}=\oint _{b}\left({\frac {\mathrm {D} }{\mathrm {D} t}}f\,\mathrm {d} {\vec {b}}+f{\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} {\vec {b}}\right)=\oint _{b}[{\dot {f}}\mathbf {I} +f\operatorname {grad} ({\vec {v}})]\cdot \,\mathrm {d} {\vec {b}}$
Vektorfeld	${\frac {\mathrm {D} }{\mathrm {D} t}}\oint _{b}{\vec {f}}\cdot \,\mathrm {d} {\vec {b}}=\oint _{b}\left({\frac {\mathrm {D} }{\mathrm {D} t}}{\vec {f}}\cdot \,\mathrm {d} {\vec {b}}+{\vec {f}}\cdot {\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} {\vec {b}}\right)=\oint _{b}[{\dot {\vec {f}}}+{\vec {f}}\cdot \operatorname {grad} ({\vec {v}})]\cdot \,\mathrm {d} {\vec {b}}$

Transportsatz für Flächenintegrale

Gegeben sei eine Fläche a mit vektoriellem Oberflächenelement $\mathrm {d} {\vec {a}}\,,$ die sich durch die Masse bewegt. Für die Fläche liege zu jeder Zeit t eine Parameterdarstellung ${\vec {a}}(\xi ,\eta ,t)$ für die Punkte auf der Fläche mit Flächenparametern (ξ,η) aus dem Einheitsquadrat [0,1]² vor. Das vektorielle Oberflächenelement berechnet sich dann mit dem Kreuzprodukt zu:

$\mathrm {d} {\vec {a}}={\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}\,\mathrm {d} \xi \,\mathrm {d} \eta \,.$

Die Zeitableitung des Flächenintegrals einer vom Ort ${\vec {x}}$ und der Zeit t abhängigen Feldgröße ${\vec {f}}({\vec {x}},t)$ über der Fläche a lautet dann:^[1]

${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{a}{\vec {f}}({\vec {a}},t)\cdot \,\mathrm {d} {\vec {a}}=&{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{0}^{1}\int _{0}^{1}{\vec {f}}({\vec {a}}(\xi ,\eta ,t),t)\cdot \left({\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}\right)\,\mathrm {d} \xi \,\mathrm {d} \eta \\=&\int _{0}^{1}\int _{0}^{1}\left[\left({\frac {\partial {\vec {f}}}{\partial {\vec {x}}}}\cdot {\frac {\partial {\vec {a}}}{\partial t}}\right)\cdot \left({\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}\right)+{\frac {\partial {\vec {f}}}{\partial t}}\cdot \left({\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}\right)+{\vec {f}}\cdot {\frac {\partial }{\partial t}}\left({\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}\right)\right]\,\mathrm {d} \xi \,\mathrm {d} \eta \\=&\int _{a}\left[{\frac {\partial {\vec {f}}}{\partial t}}+\operatorname {grad} ({\vec {f}})\cdot {\vec {v}}_{a}\right]\cdot \,\mathrm {d} {\vec {a}}+\int _{0}^{1}\int _{0}^{1}{\vec {f}}\cdot \left({\frac {\partial {\vec {v}}_{a}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}+{\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {v}}_{a}}{\partial \eta }}\right)\,\mathrm {d} \xi \,\mathrm {d} \eta \,.\end{aligned}}$

Für ein Skalarfeld gilt entsprechend:

${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{a}f({\vec {a}},t)\cdot \,\mathrm {d} {\vec {a}}=\int _{a}\left[{\frac {\partial f}{\partial t}}+\operatorname {grad} (f)\cdot {\vec {v}}_{a}\right]\,\mathrm {d} {\vec {a}}+\int _{0}^{1}\int _{0}^{1}f\cdot \left({\frac {\partial {\vec {v}}_{a}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}+{\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {v}}_{a}}{\partial \eta }}\right)\,\mathrm {d} \xi \,\mathrm {d} \eta \,.$

Wenn die Geschwindigkeit der Fläche ${\vec {v}}_{a}$ gleich der Geschwindigkeit ${\vec {v}}$ der Masse ist, dann steht in der eckigen Klammer die substantielle Zeitableitung der Feldgröße und dieser Transportsatz geht in den für von der Masse transportierte Flächen aus der Tabelle über.

Skalarfeld

${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{a}f\,\mathrm {d} {\vec {a}}=\int _{a}\left({\frac {\mathrm {D} }{\mathrm {D} t}}f\,\mathrm {d} {\vec {a}}+f{\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} {\vec {a}}\right)=\int _{a}[{\dot {f}}\mathbf {I} +f\operatorname {div} ({\vec {v}})\mathbf {I} -f\operatorname {grad} ({\vec {v}})^{\top }]\cdot \,\mathrm {d} {\vec {a}}$

Vektorfeld

${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{a}{\vec {f}}\cdot \,\mathrm {d} {\vec {a}}=\int _{a}\left({\frac {\mathrm {D} }{\mathrm {D} t}}{\vec {f}}\cdot \,\mathrm {d} {\vec {a}}+{\vec {f}}\cdot {\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} {\vec {a}}\right)=\int _{a}[{\dot {\vec {f}}}+{\vec {f}}\operatorname {div} ({\vec {v}})-{\vec {f}}\cdot \operatorname {grad} ({\vec {v}})^{\top }]\cdot \,\mathrm {d} {\vec {a}}$

Beweis

Wenn die Fläche eine materielle Fläche ist, dann gibt es eine Referenzkonfiguration mit einer zeitunabhängigen Lagrange’schen Beschreibung der Fläche ${\vec {A}}(\xi ,\eta )\,,$ die mit einer Bewegungsfunktion $\vec{\chi}$ in die aktuelle Fläche übergeht: ${\vec {a}}(\xi ,\eta ,t)={\vec {\chi }}({\vec {A}}(\xi ,\eta ),t)\,.$ Die Tangentenvektoren an die Fläche transformieren sich dann mit dem Deformationsgradient F ineinander, z.B.:^[1]

${\frac {\partial {\vec {a}}(\xi ,\eta ,t)}{\partial \xi }}={\frac {\partial {\vec {\chi }}({\vec {A}}(\xi ,\eta ),t)}{\partial \xi }}={\frac {\partial {\vec {\chi }}({\vec {X}},t)}{\partial {\vec {X}}}}\cdot {\frac {\partial {\vec {A}}(\xi ,\eta )}{\partial \xi }}=\mathbf {F} \cdot {\frac {\partial {\vec {A}}(\xi ,\eta )}{\partial \xi }}\,.$

Der im Transportsatz im zweiten Integranden auftauchende Term vereinfacht sich damit zu:

${\begin{aligned}\left({\frac {\partial {\vec {v}}_{a}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}+{\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {v}}_{a}}{\partial \eta }}\right)\,\mathrm {d} \xi \,\mathrm {d} \eta =&{\frac {\partial }{\partial t}}\left({\frac {\partial {\vec {a}}}{\partial \xi }}\times {\frac {\partial {\vec {a}}}{\partial \eta }}\right)\,\mathrm {d} \xi \,\mathrm {d} \eta ={\frac {\partial }{\partial t}}\left[\left(\mathbf {F} \cdot {\frac {\partial {\vec {A}}}{\partial \xi }}\right)\times \left(\mathbf {F} \cdot {\frac {\partial {\vec {A}}}{\partial \eta }}\right)\right]\,\mathrm {d} \xi \,\mathrm {d} \eta \\=&{\frac {\partial }{\partial t}}\operatorname {cof} (\mathbf {F} )\cdot \left({\frac {\partial {\vec {A}}}{\partial \xi }}\times {\frac {\partial {\vec {A}}}{\partial \eta }}\right)\,\mathrm {d} \xi \,\mathrm {d} \eta ={\frac {\partial }{\partial t}}[\operatorname {det} (\mathbf {F} )\mathbf {F} ^{\top -1}]\cdot \,\mathrm {d} {\vec {A}}={\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} {\vec {a}}\,,\end{aligned}}$

siehe die Berechnung des Kreuzprodukts und des Kofaktors cof mit dem äußeren Tensorprodukt und die Zeitableitung von Linien-, Flächen- und Volumenelementen. Es wurde ausgenutzt, dass in der Lagrange’schen Betrachtungsweise die partielle Zeitableitung gleich der substantiellen Zeitableitung ist. Mit diesem Ergebnis geht der obige Transportsatz in den für von der Masse transportierte Flächen über.

Reynolds’scher Transportsatz oder Transportsatz für Volumenintegrale

Der Reynolds’sche Transportsatz wird verwendet, um grundlegende Erhaltungssätze der Kontinuumsmechanik herzuleiten. Wird z.B. die Dichte ρ für das Skalarfeld f eingesetzt, dann ergibt sich eine Formulierung für die Massenerhaltung.

Gegeben sei ein Kontrollvolumen V_k mit Volumenelement dV_k und Oberfläche a_k mit nach außen gerichtetem, vektoriellem Oberflächenelement $\mathrm {d} {\vec {a}}_{k}\,,$ die sich durch die Masse bewegen. Dann lautet die Zeitableitung des Volumenintegrals einer vom Ort ${\vec {x}}$ und der Zeit t abhängigen Feldgröße ${\vec {f}}({\vec {x}},t)$ über das Kontrollvolumen, oder kurz der Reynolds’sche Transportsatz:

Skalarfeld	${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}}f\,\mathrm {d} V_{k}=\int _{V_{k}}{\frac {\partial f}{\partial t}}\,\mathrm {d} V_{k}+\int _{a_{k}}f\,({\vec {v}}_{k}\cdot \,\mathrm {d} {\vec {a}}_{k})$
Vektorfeld	${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}}{\vec {f}}\,\mathrm {d} V_{k}=\int _{V_{k}}{\frac {\partial {\vec {f}}}{\partial t}}\,\mathrm {d} V_{k}+\int _{a_{k}}{\vec {f}}\,({\vec {v}}_{k}\cdot \,\mathrm {d} {\vec {a}}_{k})$

Das Volumen V wird hier wie im Folgenden groß geschrieben, um eine Verwechslung mit der Geschwindigkeit ${\vec {v}}$ zu vermeiden.

Der Reynolds’sche Transportsatz kann wie folgt interpretiert werden: Die zeitliche Änderung des Inhalts einer Feldgröße in einem variablen Kontrollvolumen setzt sich aus einem lokalen und einem konvektiven Anteil zusammen. Der lokale Anteil besteht aus dem Integral über die lokale Zeitableitung, die mit der partiellen Ableitung gebildet wird, und der konvektive Anteil bestimmt sich aus dem Transport der Feldgröße über die Grenze a_k des Kontrollvolumens. Mit $\mathrm {d} {\vec {a}}_{k}=|\,\mathrm {d} {\vec {a}}_{k}|{\vec {n}}$ ist ${\vec {f}}({\vec {v}}_{k}\cdot {\vec {n}})$ die Übergangsmenge pro Zeit- und Flächeneinheit.

Beweis

Für die Raumpunkte im Volumen liege zu jeder Zeit t eine eineindeutige Parameterdarstellung ${\vec {x}}({\vec {\Theta }},t)$ mit Parametern ${\vec {\Theta }}\in [0,1]^{3}$ vor. Das Volumenelement berechnet sich dann mit dem Spatprodukt zu:^[1]

${\begin{aligned}\mathrm {d} V_{k}=&{\frac {\partial {\vec {x}}}{\partial \Theta _{1}}}\cdot \left({\frac {\partial {\vec {x}}}{\partial \Theta _{2}}}\times {\frac {\partial {\vec {x}}}{\partial \Theta _{3}}}\right)\,\underbrace {\mathrm {d} \Theta _{1}\,\mathrm {d} \Theta _{2}\,\mathrm {d} \Theta _{3}} _{\mathrm {d} \Omega }=\operatorname {det} {\begin{pmatrix}{\frac {\partial {\vec {x}}}{\partial \Theta _{1}}}&{\frac {\partial {\vec {x}}}{\partial \Theta _{2}}}&{\frac {\partial {\vec {x}}}{\partial \Theta _{3}}}\end{pmatrix}}\,\mathrm {d} \Omega \\=&\operatorname {det} \left({\frac {\partial {\vec {x}}}{\partial {\vec {\Theta }}}}\right)\,\mathrm {d} \Omega =:\operatorname {det} (\mathbf {J} )\,\mathrm {d} \Omega \,.\end{aligned}}$
Die Ableitung J des Ortes nach den Koordinaten ${\vec {\Theta }}$ berechnet sich wie eine Jacobi-Matrix. Die Zeitableitung des Volumenintegrals einer vom Ort ${\vec {x}}$ und der Zeit t abhängigen Feldgröße ${\vec {f}}({\vec {x}},t)$ über das Volumen V_k lautet dann:^[1]
${\begin{aligned}{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}}{\vec {f}}({\vec {x}},t)\,\mathrm {d} V_{k}=&{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}{\vec {f}}({\vec {x}}({\vec {\Theta }},t),t)\cdot \operatorname {det} (\mathbf {J} )\,\mathrm {d} \Omega \\=&\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}\left[{\frac {\partial {\vec {f}}}{\partial {\vec {x}}}}\cdot {\frac {\partial {\vec {x}}}{\partial t}}\operatorname {det} (\mathbf {J} )+{\frac {\partial {\vec {f}}}{\partial t}}\operatorname {det} (\mathbf {J} )+{\vec {f}}\cdot \operatorname {det} (\mathbf {J} )\left(\mathbf {J} ^{\top -1}:{\frac {\partial \mathbf {J} }{\partial t}}\right)\right]\,\mathrm {d} \Omega \\=&\int _{V_{k}}\left[{\frac {\partial {\vec {f}}}{\partial t}}+\operatorname {grad} ({\vec {f}})\cdot {\vec {v}}_{k}+{\vec {f}}\operatorname {div} ({\vec {v}}_{k})\right]\,\mathrm {d} V_{k}\,,\end{aligned}}$
denn die Ableitung der Determinante eines Tensors nach dem Tensor berechnet sich zu^[1] ${\tfrac {\mathrm {d} }{\mathrm {d} \mathbf {T} }}\operatorname {det} \mathbf {T} =\operatorname {det} (\mathbf {T} )\mathbf {T} ^{\top -1}$ und
${\begin{aligned}\mathbf {J} ^{\top -1}:{\frac {\partial \mathbf {J} }{\partial t}}:=&\operatorname {Sp} \left(\mathbf {J} ^{-1}\cdot {\frac {\partial \mathbf {J} }{\partial t}}\right)=\operatorname {Sp} \left({\frac {\partial \mathbf {J} }{\partial t}}\cdot \mathbf {J} ^{-1}\right)=\operatorname {Sp} \left({\frac {\partial {\vec {v}}_{k}}{\partial {\vec {\Theta }}}}\cdot {\frac {\mathrm {d} {\vec {\Theta }}}{\mathrm {d} {\vec {x}}}}\right)=\operatorname {Sp} \left({\frac {\partial {\vec {v}}_{k}}{\partial {\vec {x}}}}\right)=\operatorname {div} ({\vec {v}}_{k})\,.\end{aligned}}$
Der Operator Sp bildet die Spur seines Arguments und die Geschwindigkeit im Kontrollvolumen ist die Zeitableitung ${\vec {v}}_{k}:={\tfrac {\partial }{\partial t}}{\vec {x}}({\vec {\Theta }},t)\,.$ Ferner ist die Spur des Geschwindigkeitsgradienten die Divergenz des Geschwindigkeitsfeldes. Für ein Skalarfeld gilt entsprechend:
${\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}}f({\vec {x}},t)\,\mathrm {d} V_{k}=\int _{V_{k}}\left[{\frac {\partial f}{\partial t}}+\operatorname {grad} (f)\cdot {\vec {v}}_{k}+f\operatorname {div} ({\vec {v}}_{k})\right]\,\mathrm {d} V_{k}\,.$
Mit der Produktregel
$\operatorname {div} (f{\vec {v}})=\operatorname {grad} (f)\cdot {\vec {v}}+f\operatorname {div} ({\vec {v}})\quad {\text{bzw.}}\quad \operatorname {div} ({\vec {v}}\otimes {\vec {f}})=\operatorname {grad} ({\vec {f}})\cdot {\vec {v}}+\operatorname {div} ({\vec {v}}){\vec {f}}$
und dem Gauß’schen Integralsatz
$\int _{v}\operatorname {div} (f{\vec {v}})\,\mathrm {d} v=\int _{a}f{\vec {v}}\cdot \,\mathrm {d} {\vec {a}}\quad {\text{bzw.}}\quad \int _{v}\operatorname {div} ({\vec {v}}\otimes {\vec {f}})\,\mathrm {d} v=\int _{a}{\vec {f}}({\vec {v}}\cdot \,\mathrm {d} {\vec {a}})$
können diese Integrale weiter umgeformt werden und es ergeben sich die Resultate in der Tabelle. Das Rechenzeichen „ $\otimes$ “ bildet das dyadische Produkt.
In der Literatur kommt auch ein Divergenzoperator $\operatorname {\tilde {div}}$ für Tensoren vor, der die Divergenz der Zeilen des Tensors bildet und nicht – wie hier – der Spalten. Mit dem Operator gilt:
$\operatorname {\tilde {div}} ({\vec {f}}\otimes {\vec {v}})=\operatorname {grad} ({\vec {f}})\cdot {\vec {v}}+\operatorname {div} ({\vec {v}}){\vec {f}}\quad {\text{und}}\quad \int _{v}\operatorname {\tilde {div}} ({\vec {f}}\otimes {\vec {v}})\,\mathrm {d} v=\int _{a}{\vec {f}}({\vec {v}}\cdot \,\mathrm {d} {\vec {a}})\,,$
so dass das Endergebnis wieder übereinstimmt.

Wenn die Geschwindigkeit ${\vec {v}}_{k}$ des Kontrollvolumens gleich der Geschwindigkeit ${\vec {v}}$ der Masse ist (kein Ein- und Ausfluss von Materie), dann geht dieser Transportsatz in den für von der Masse transportierte Volumen aus der Tabelle über.

Skalarfeld

${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V}f\,\mathrm {d} V=\int _{V}\left({\frac {\mathrm {D} }{\mathrm {D} t}}f\,\mathrm {d} V+f{\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} V\right)=\int _{V}[{\dot {f}}+f\operatorname {div} ({\vec {v}})]\,\mathrm {d} V=\int _{V}{\frac {\partial f}{\partial t}}\,\mathrm {d} V+\int _{a}f{\vec {v}}\cdot \,\mathrm {d} {\vec {a}}$

Vektorfeld

${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V}{\vec {f}}\,\mathrm {d} V=\int _{V}\left({\frac {\mathrm {D} }{\mathrm {D} t}}{\vec {f}}\cdot \,\mathrm {d} V+{\vec {f}}\cdot {\frac {\mathrm {D} }{\mathrm {D} t}}\,\mathrm {d} V\right)=\int _{V}[{\dot {\vec {f}}}+{\vec {f}}\operatorname {div} ({\vec {v}})]\,\mathrm {d} V=\int _{V}{\frac {\partial {\vec {f}}}{\partial t}}\,\mathrm {d} V+\int _{a}{\vec {f}}({\vec {v}}\cdot \,\mathrm {d} {\vec {a}})$

Dies ist der Reynolds’sche Transportsatz spezialisiert auf von Massen mitgeführten Volumina V. Hier ist a die Oberfläche der Masse mit nach außen gerichtetem, vektoriellem Oberflächenelement $\mathrm {d} {\vec {a}}\,.$

Wenn die Grenzen des Kontrollvolumens und der Masse zu einem Zeitpunkt übereinstimmen, dann kann aus dem allgemeinen Reynolds’schen Transportsatz und der spezialisieren, letzteren Version der lokale Anteil eliminiert werden:

Skalarfeld	${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V}f\,\mathrm {d} V={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}}f\,\mathrm {d} V_{k}+\int _{a_{k}}f\;({\vec {v}}-{\vec {v}}_{k})\cdot \,\mathrm {d} {\vec {a}}_{k}$
Vektorfeld	${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V}{\vec {f}}\,\mathrm {d} V={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}}{\vec {f}}\,\mathrm {d} V_{k}+\int _{a_{k}}{\vec {f}}\;[({\vec {v}}-{\vec {v}}_{k})\cdot \,\mathrm {d} {\vec {a}}_{k}]$

Die materielle Zeitableitung des Inhalts einer Feldgröße in einem Volumen ist demnach gleich der zeitlichen Änderung im zeitabhängigen Volumen V_k und dem Transport über die wandernde Fläche a_k mit einer Durchflussmenge, die von der Geschwindigkeitsdifferenz ${\vec {v}}-{\vec {v}}_{k}$ zwischen den Partikeln der Masse und der Fläche a_k in Richtung der Flächennormalen bestimmt ist.

Einfluss von Sprungstellen

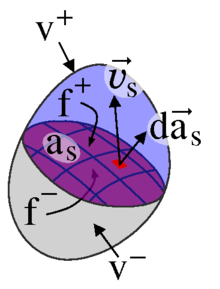
Eine Sprungstelle auf der Fläche a_s trennt zwei Raumbereiche V⁺ und V⁻

Die eingangs verlangte örtliche stetige Differenzierbarkeit des transportierten Feldes wird unter realen Verhältnissen verletzt, wenn beispielsweise Dichtesprünge an Materialgrenzen oder Stoßwellen auftreten. Solche flächigen Sprungstellen können jedoch im Transportsatz berücksichtigt werden, wenn die Fläche selbst örtlich stetig differenzierbar ist und so in jedem ihrer Punkte einen Normalenvektor besitzt. Die Fläche – im folgenden Sprungstelle genannt – muss keine materielle Fläche sein, kann sich also mit einer anderen Geschwindigkeit bewegen als die Masse selbst. Durch diese Fläche wird die Masse in zwei Stücke V⁺ und V⁻ geteilt und es wird vereinbart, dass der Normalenvektor der Sprungstelle a_s in Richtung der Sprungstellengeschwindigkeit und das Volumen V⁺ weise, siehe Bild rechts.

Dann ergibt sich der Transportsatz für Fälle mit Sprungstelle aus der Tabelle.

Skalarfeld	${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V}f\,\mathrm {d} V=\int _{V}{\frac {\partial f}{\partial t}}\,\mathrm {d} V+\int _{a}f\;({\vec {v}}\cdot \,\mathrm {d} {\vec {a}})-\int _{a_{s}}[[f\;(({\vec {v}}-{\vec {v}}_{s})\cdot {\vec {n}})]]\mathrm {d} a_{s}$
Vektorfeld	${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V}{\vec {f}}\,\mathrm {d} V=\int _{V}{\frac {\partial {\vec {f}}}{\partial t}}\,\mathrm {d} V+\int _{a}{\vec {f}}\;({\vec {v}}\cdot \,\mathrm {d} {\vec {a}})-\int _{a_{s}}[[{\vec {f}}\;(({\vec {v}}-{\vec {v}}_{s})\cdot {\vec {n}})]]\mathrm {d} a_{s}$

Der neu hinzugekommene letzte Term integriert die Sprungfunktion über die Sprungstelle, beispielsweise:

$[[f\;(({\vec {v}}-{\vec {v}}_{s})\cdot {\vec {n}})]]:=f^{+}\;(({\vec {v}}^{+}-{\vec {v}}_{s})\cdot {\vec {n}})-f^{-}\;(({\vec {v}}^{-}-{\vec {v}}_{s})\cdot {\vec {n}})\,.$

Die Größe f⁺ ist der Wert des interessierenden Felds bei Annäherung an die Sprungstelle in V⁺, f⁻ ist die Größe bei Annäherung an die Sprungstelle in V⁻ und so macht das Feld auf der Fläche a_s den Sprung [[f]]:=f⁺ - f⁻. Gleiches gilt für die Geschwindigkeit, die beispielsweise bei einer Stoßwelle auf beiden Seiten der Sprungstelle verschieden sein kann. Die Sprungstellengeschwindigkeit ${\vec {v}}_{s}$ und die Normale ${\vec {n}}$ an die Sprungstelle – definiert mit $\mathrm {d} {\vec {a}}_{s}=|\,\mathrm {d} {\vec {a}}_{s}|{\vec {n}}=:{\vec {n}}\,\mathrm {d} a_{s}$ – sind auf beiden Seiten der Sprungstelle identisch. Das Minuszeichen vor dem letzten Integral geht aus der Vereinbarung hervor, dass die Normale an die Sprungstelle und die Sprungstellengeschwindigkeit in das Volumen V⁺ weisen.

Beweis

Gegeben ist eine örtlich stetig differenzierbare Fläche a_s, die sich mit der ihr eigenen Sprungstellengeschwindigkeit ${\vec {v}}_{s}$ durch die Masse hindurch bewegt, siehe Bild. Die Oberfläche des gesamten Kontrollvolumens V (die innere Fläche a_s zählt nicht dazu) besteht aus dem zum Volumen V⁺ gehörenden Teil a⁺ und dem Komplement a⁻ und bewege sich mit der Masse mit, so dass die Oberflächen materielle Flächen darstellen. Nur auf der Sprungstelle habe die Oberfläche der Kontrollvolumina die ihnen eigene Sprungstellengeschwindigkeit. Anwendung des Reynold’schen Transportsatzes in der Form

${\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V}{\vec {f}}\,\mathrm {d} V={\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}}{\vec {f}}\,\mathrm {d} V_{k}+\int _{a_{k}}{\vec {f}}[({\vec {v}}-{\vec {v}}_{k})\cdot \,\mathrm {d} {\vec {a}}_{k}]$
auf die beiden Teilvolumina liefert
${\begin{aligned}{\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V^{+}}{\vec {f}}\,\mathrm {d} {V^{+}}=&{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}^{+}}{\vec {f}}\,\mathrm {d} V_{k}^{+}+\int _{a_{k}^{+}}{\vec {f}}[(\underbrace {{\vec {v}}-{\vec {v}}_{k}^{+}} _{={\vec {0}}})\cdot \,\mathrm {d} {\vec {a}}_{k}^{+}]-\int _{a_{s}}{\vec {f}}^{+}[({\vec {v}}^{+}-{\vec {v}}_{s})\cdot \,\mathrm {d} {\vec {a}}_{s}]\\{\frac {\mathrm {D} }{\mathrm {D} t}}\int _{V^{-}}{\vec {f}}\,\mathrm {d} {V^{-}}=&{\frac {\mathrm {d} }{\mathrm {d} t}}\int _{V_{k}^{-}}{\vec {f}}\,\mathrm {d} V_{k}^{-}+\int _{a_{k}^{-}}{\vec {f}}[(\overbrace {{\vec {v}}-{\vec {v}}_{k}^{-}} )\cdot \,\mathrm {d} {\vec {a}}_{k}^{-}]+\int _{a_{s}}{\vec {f}}^{-}[({\vec {v}}^{-}-{\vec {v}}_{s})\cdot \,\mathrm {d} {\vec {a}}_{s}]\,,\end{aligned}}$
denn das Oberflächenelement soll immer nach außen gerichtet sein und geht daher auf der Sprungstelle einmal mit negativem und einmal mit positivem Vorzeichen ein. Die mit den geschweiften Klammern markiertenTerme verschwinden nach Voraussetzung. Addition der Terme auf der linken Seite der beiden Gleichungen liefert die materielle Zeitableitung des Volumenintegrals mit Sprungstelle. Für die Summe der ersten Terme auf den rechten Seiten wird der Transportsatz für Kontrollvolumen eingesetzt. Als Resultat ergibt sich der Transportsatz für Fälle mit Sprungstelle aus der obigen Tabelle.

Fußnoten

↑ ^a ^b ^c ^d ^e ^f ^g Die Fréchet-Ableitung einer Funktion nach ist der beschränkte lineare Operator ${\mathcal {A}}$ der - sofern er existiert - in alle Richtungen dem Gâteaux-Differential entspricht, also

${\mathcal {A}}(h)=\left.{\frac {{\mathrm {d}}}{{\mathrm {d}}s}}f(x+sh)\right|_{{s=0}}=\lim _{{s\rightarrow 0}}{\frac {f(x+sh)-f(x)}{s}}\quad \forall \;h$
gilt. Darin ist $s\in {\mathbb {R}}\,,f,x\,{\textsf {und}}\,h$ skalar-, vektor- oder tensorwertig aber und gleichartig. Dann wird auch

${\mathcal {A}}={\frac {\partial f}{\partial x}}$
geschrieben.

Basierend auf einem Artikel in:

Wikipedia.de