
Logarithmische Normalverteilung
Die logarithmische Normalverteilung (kurz Log-Normalverteilung)
ist eine kontinuierliche Wahrscheinlichkeitsverteilung
über der Menge der positiven reellen
Zahlen. Sie beschreibt die Verteilung einer Zufallsvariablen
,
wenn
normalverteilt
ist. Umgekehrt, wenn
normalverteilt ist, so ist
logarithmisch normalverteilt.
Im Gegensatz zu einer normalverteilten Zufallsvariablen, die nach dem zentralen Grenzwertsatz als Summe vieler verschiedener Zufallsvariablen aufgefasst werden kann, entsteht eine logarithmisch normalverteilte Zufallsvariable durch das Produkt vieler positiver Zufallsvariablen. Somit ist die logarithmische Normalverteilung die einfachste Verteilungsart für multiplikative Modelle.
Definition
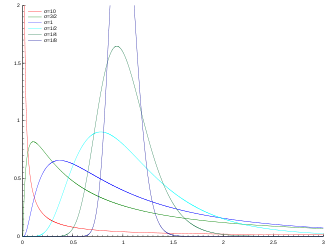
Dichtefunktion
Eine stetige Zufallsvariable
unterliegt der logarithmischen Normalverteilung
mit den Parametern
und
,
wenn sie die Wahrscheinlichkeitsdichte
besitzt.
Zweidimensionale Log-Normalverteilung
Sind
und
zwei log-normalverteilte Zufallsvariable, dann ist mit dem transformierten Korrelationskoeffizienten
deren gemeinsame Wahrscheinlichkeitsdichte definiert als
.
Verteilungsfunktion
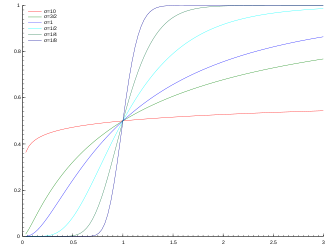
Damit hat die logarithmische Normalverteilung für
die Verteilungsfunktion
,
wobei
die Verteilungsfunktion der Standardnormalverteilung
bezeichnet.
Die Verteilungsfunktion der logarithmischen Normalverteilung erscheint auf doppelt logarithmisch geteiltem Wahrscheinlichkeitspapier als Gerade.
Eigenschaften
Logarithmus
Der Logarithmus von
ist normalverteilt, denn
mit der Verteilungsfunktion
der Standardnormalverteilung.
Maximum
Die Wahrscheinlichkeitsdichte nimmt ihren maximalen Wert
an der Stelle
an.
Erwartungswert
Der Erwartungswert der logarithmischen Normalverteilung beträgt
Varianz
Die Varianz ergibt sich analog zu
.
Standardabweichung
Für die Standardabweichung ergibt sich
>.
Variationskoeffizient
Aus Erwartungswert und Varianz erhält man unmittelbar den Variationskoeffizienten
.
Schiefe
Die Schiefe ergibt sich zu
,
d.h., die Lognormalverteilung ist rechtsschief.
Quantile
Ist
das p-Quantil
einer Standardnormalverteilung
(d.h.
,
wobei
die Verteilungsfunktion der Standardnormalverteilung sei), so ist das p-Quantil
der Logarithmischen Normalverteilung gegeben durch
.
Insbesondere ist der Median, d.h. der Wert, bei dem die Verteilungsfunktion den Wert 0,5 annimmt, gegeben durch
.
Je größer die Differenz
zwischen Erwartungswert und Median, desto ausgeprägter ist i.a. die Schiefe einer
Verteilung. Hier unterscheiden sich diese Parameter um den Faktor .
Die Wahrscheinlichkeit für extrem große Ausprägungen ist also bei der
Lognormalverteilung hoch.
Charakteristische Funktion
Die charakteristische Funktion ist für die logarithmische Normalverteilung nicht explizit darstellbar.
Momente
Für die logarithmische Normalverteilung existieren alle Momente und es gilt:
.
Momenterzeugende Funktion
Die momenterzeugende Funktion existiert nicht für die logarithmische Normalverteilung.
Entropie
Die Entropie der logarithmischen Normalverteilung (ausgedrückt in nats) beträgt
.
Beziehungen zu anderen Verteilungen
Beziehung zur Normalverteilung
Der Logarithmus einer logarithmisch-normalverteilten Zufallsvariablen ist
normalverteilt. Genauer: Ist
eine
-verteilte
reelle Zufallsvariable (d.h. normalverteilt mit Erwartungswert
und Varianz
),
so ist die Zufallsvariable
Log-normalverteilt mit diesen Parametern
und
,
allerdings bilden diese Parameter nicht Erwartungswert und Varianz von
.
Ist ein bestimmter Erwartungswert und eine bestimmte Varianz gewünscht, so kann
man dies leicht durch die folgenden Formeln erreichen:
und
oder direkt
Anwendungen
Black-Scholes-Modell
Im Black-Scholes-Modell folgen Aktienkurse einer geometrischen brownschen Bewegung und sind damit logarithmisch normalverteilt. In diesem Modell lassen sich explizit Preise von Finanzoptionen bestimmen.
Einkommensverteilung
Häufig sind Einkommen lognormalverteilt. Ein Grund ist, dass es relativ wenig bestbezahlte Stellen gegenüber sehr vielen Arbeitsstellen mit eher geringem Einkommen gibt, wobei besonders niedrige Einkommen wieder seltener werden. Das entspricht genau dem Verlauf der meisten Lognormalverteilungen. Dieser Umstand kann in jedem operativ funktionierenden Unternehmen überprüft werden.
Schätzung von Umsatzziffern von Unternehmen
Die Logarithmen aller Fakturenbeträge eines Unternehmens folgen annähernd einer Normalverteilung. Der Abstand zwischen dem Logarithmus des kleinsten und dem Logarithmus des größten Fakturenbetrages repräsentiert annähernd die 6-fache Standardabweichung der Normalverteilung der Logarithmen. Dadurch ist es möglich, auf den Mittelwert oder Erwartungswert der Fakturenbeträge (s.o.) der Lognormalverteilung zu schließen. Multiplikation dieses Mittelwertes mit der Anzahl der gültigen Fakturen ergibt in den meisten Fällen einen akzeptablen Schätzwert für die Größenordnung des Umsatzes eines Unternehmens; wertmäßig liegt er tendenziell zu hoch: Da für solche Schätzungen häufig auch das benfordsche Gesetz gelten sollte, sollte in diesen Fällen auch die Benford-Verteilung zu Rate gezogen werden. Dabei ist zu beachten, dass die Größenordnungen (Stellenwerte) der Rechnungsbeträge nicht gleichverteilt, sondern annähernd normalverteilt sind.
Versicherungsmathematik
In der Versicherungsmathematik wird die Verteilung der Schadensanzahl häufig mit Hilfe von Zufallsvariablen modelliert, die der Poisson-Verteilung oder der Negativ-Binomialverteilung genügen. Dagegen eignen sich zur Modellierung der Schadenshöhe insbesondere die Gammaverteilung, die Log-Gammaverteilung oder die Log-Normalverteilung.
Die logarithmische Normalverteilung wird wegen der oben besprochenen Schiefe und der damit verbundenen Großschadenneigung bei der Modellierung von Risiken häufig als Verteilung der Schadenshöhe eingesetzt. Sind der Erwartungswert E und die Standardabweichung stdev vorgegeben, so erhält man die Parameter der logarithmischen Normalverteilung wie folgt:
und
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.11. 2022