
Dynkin-System
Ein Dynkin-System (manchmal auch λ-System genannt) ist ein Begriff aus der Maßtheorie, einem Teilgebiet der Mathematik. Es ist benannt nach dem russischen Mathematiker Eugene Dynkin. Sie sind in Kombination mit dem Dynkinschen π-λ-Satz ein wichtiges Hilfsmittel zur Herleitung von Eindeutigkeitsaussagen in der Maßtheorie und Stochastik (siehe Maßeindeutigkeitssatz)
Definition
Eine Teilmenge
der Potenzmenge
einer nichtleeren Grundmenge
heißt Dynkin-System über
,
falls sie die folgenden Eigenschaften besitzt:
- Das System enthält die Grundmenge:
-
.
- Das System ist abgeschlossen unter Bildung von Komplementen:
-
.
- Das System ist abgeschlossen bezüglich abzählbarer Vereinigungen paarweise disjunkter Mengen:
-
disjunkt
.
δ-Operator
Beliebige Durchschnitte von Dynkin-Systemen über
ergeben wieder ein Dynkin-System. Ist daher
ein Mengensystem, dann wird durch
ein Dynkin-System
definiert, genannt das von
erzeugte Dynkin-System. Es ist das kleinste Dynkin-System, welches
enthält.
heißt Erzeuger von
.
Der δ-Operator ist ein Hüllenoperator.
Teilweise wird er entsprechend der Namensgebung als -System
auch als
-Operator
notiert. Weitere alternative Bezeichnungen sind
oder
.
Das Dynkin-System-Argument
Mit Dynkin-Systemen lassen sich in vielen Fällen Aussagen über σ-Algebren
relativ einfach beweisen. Sei
eine Aussage, die für Mengen
entweder zutrifft oder nicht. Weiter sei
eine σ-Algebra mit einem durchschnittsstabilen Erzeuger
,
für dessen Elemente man
zeigen kann. Nach dem Prinzip
der guten Mengen betrachtet man nun das Mengensystem
und zeigt, dass es ein Dynkin-System ist. Dann folgt wegen der
Durchschnittsstabilität von
einerseits
,
andererseits gilt aber auch
und damit wegen
schon
.
Die definierenden Eigenschaften eines Dynkin-Systems sind oft einfacher nachzuweisen, weil bei der Abgeschlossenheit gegenüber abzählbarer Vereinigung nur Folgen von paarweise disjunkten Einzelmengen betrachtet werden müssen, während bei σ-Algebren diese Zusatzeigenschaft nicht zur Verfügung steht.
Zusammenhang mit weiteren Mengensystemen
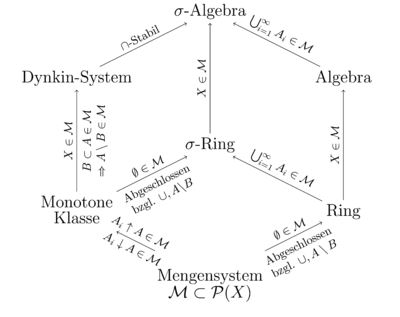
σ-Algebren
Jede σ-Algebra ist immer auch ein Dynkin-System. Umgekehrt ist jedes durchschnittsstabile Dynkinsystem auch eine σ-Algebra. Ein Beispiel für ein Dynkin-System, das keine σ-Algebra ist, ist
auf der Grundmenge .
Das Mengensystem ist ein Dynkin-System, aber keine Algebra (da nicht
Schnittstabil) und damit auch keine σ-Algebra.
Es gilt außerdem der Dynkinsche
π-λ-Satz: Ist
ein durchschnittsstabiles Mengensystem, so stimmen die von
erzeugte
σ-Algebra und das von
erzeugte Dynkin-System überein.
Monotone Klassen
Dynkin-Systeme lassen sich auch über monotone
Klassen definieren: Ein Mengensystem
ist genau dann ein Dynkin-System, wenn
eine monotone Klasse ist, welche die Obermenge
enthält, und in der für beliebige Mengen
mit
gilt, dass auch
ist.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 30.08. 2017