Persymmetrische Matrix

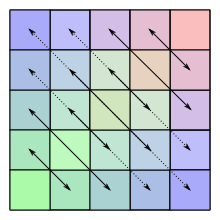
Symmetriemuster einer persymmetrischen (5×5)-Matrix

Eine persymmetrische Matrix ist in der Mathematik eine quadratische Matrix, die symmetrisch bezüglich ihrer Gegendiagonale ist.

Definition

Eine quadratische Matrix $A\in K^{n\times n}$ über einem Körper heißt persymmetrisch, wenn für ihre Einträge

$a_{i,j} = a_{n-j+1,n-i+1}$

für $i,j = 1, \ldots, n$ gilt. Die Einträge einer persymmetrischen Matrix verändern sich demnach nicht, wenn sie an der Gegendiagonale gespiegelt werden.

Beispiele

Eine reelle persymmetrische Matrix der Größe $3\times 3$ ist beispielsweise

$A = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 2 \\ 3 & 2 & 1 \end{pmatrix}$

Allgemein haben persymmetrische Matrizen der Größe $3\times 3$ die Form

$A = \begin{pmatrix} a & b & c \\ d & e & b \\ f & d & a \end{pmatrix}$

mit $a,b,c,d,e,f \in K$ .

Eigenschaften

Symmetrien

Mit der Permutationsmatrix $J \in K^{n \times n}$ definiert durch

$J=(\delta _{i,n-j+1})_{ij}={\begin{pmatrix}0&&1\\&\cdot ^{\,\cdot ^{\,\cdot }}&\\1&&0\end{pmatrix}}$

lassen sich persymmetrische Matrizen auch kompakt durch die Bedingung

charakterisieren. Eine bisymmetrische Matrix ist eine persymmetrische Matrix, die zudem symmetrisch oder zentralsymmetrisch ist. Eine Toeplitz-Matrix ist eine persymmetrische Matrix, deren Einträge auf der Hauptdiagonale und allen Nebendiagonalen konstant sind. Eine zyklische Matrix ist eine persymmetrische Matrix, deren Einträge auf allen Diagonalen konstant sind und sich zyklisch wiederholen.

Summe und Produkt

Die Summe A+B zweier persymmetrischer Matrizen und ergibt wieder eine persymmetrische Matrix, ebenso sind auch skalare Vielfache mit $c\in K$ . Nachdem die Nullmatrix trivialerweise persymmetrisch ist, bilden die persymmetrischen Matrizen einen Untervektorraum im Matrizenraum $K^{n \times n}$ .

Das Produkt $A\cdot B$ zweier persymmetrischer Matrizen ergibt aufgrund von

genau dann wieder eine persymmetrische Matrix, wenn die beiden Matrizen und kommutieren.

Inverse

Für die Inverse $A^{-1}$ einer persymmetrischen Matrix gilt, sofern sie existiert

$J A^{-1} = (A J)^{-1} = (J A^T)^{-1} = A^{-T} J$ .

Die Inverse einer regulären persymmetrischen Matrix ist demnach wieder persymmetrisch.

Siehe auch

Hankel-Matrix

Literatur

Martin Hanke-Bourgeois: Grundlagen der Numerischen Mathematik und des Wissenschaftlichen Rechnens. Springer, 2008, ISBN 978-3-8348-0708-3.
Roger A. Horn, Charles R. Johnson: Matrix Analysis. Cambridge University Press, 2012, ISBN 978-0-521-83940-2.

Basierend auf einem Artikel in:

Wikipedia.de