Hankel-Matrix

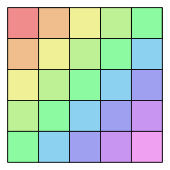
Besetzungsmuster einer Hankel-Matrix der Größe 5×5

Eine Hankel-Matrix, benannt nach Hermann Hankel (1839–1873), bezeichnet eine quadratische Matrix, bei der auf jeder von rechts oben nach links unten verlaufenden Gegendiagonalen jeweils nur ein konstanter Wert auftritt. Sie ist also durch die oberste Zeile und die äußerste rechte Spalte der Matrix vollständig beschrieben.

Eine Hankel-Matrix ist eine symmetrische Matrix. Die Dimension des Vektorraums der $n\times n$ Hankel-Matrizen ist 2n-1 .

Diese Vereinfachung erlaubt ebenso wie bei den verwandten Toeplitz-Matrizen den Einsatz besonders effizienter Verfahren für Matrixoperationen wie Multiplikation und Inversion.

Beispiel

Hier ein Beispiel einer $4\times 4$ -Hankel-Matrix:

$M={\begin{pmatrix}1&2&3&4\\2&3&4&5\\3&4&5&6\\4&5&6&7\\\end{pmatrix}}$

Ein sehr bekanntes Beispiel einer Hankel-Matrix ist die Hilbert-Matrix.

Basierend auf einem Artikel in:

Wikipedia.de