Quotientenkörper
In der Algebra ist der
Quotientenkörper eines Rings
(mit bestimmten Eigenschaften) eine Obermenge dieses Rings, auf welche die Addition und
die Multiplikation
des Rings fortgesetzt werden und in der jedes Element außer
ein multiplikatives Inverses
besitzt. Das prominenteste Beispiel ist der Körper der rationalen Zahlen als
Quotientenkörper des Rings der ganzen
Zahlen. Eine Verallgemeinerung des Konzepts für nicht notwendigerweise
nullteilerfreie Ringe ist durch die Lokalisierung
gegeben.
Definition
Es sei
ein vom Nullring verschiedener, nullteilerfreier kommutativer Ring.
Der kleinste Körper,
in den
eingebettet werden kann, wird der Quotientenkörper oder Körper der
Brüche des Rings genannt. Gebräuchlich ist die symbolische Abkürzung
oder auch
.
Bemerkungen
Für den Nullring wäre die Menge
in der Definition unten leer. Der Ring muss frei von Nullteilern sein, da
ansonsten für
mit
die Multiplikation nicht wohldefiniert wäre (siehe unten). Ist der Ring nicht
kommutativ, so entsteht lediglich ein Schiefkörper,
der nicht zwangsläufig ein Körper ist.
Jeder Ring obiger Art kann in einen „kleinsten“ Körper eingebettet werden,
d.h. alle Körper, in die der Ring eingebettet werden kann, enthalten einen
zu diesem kleinsten Körper, dem Quotientenkörper des Rings, isomorphen
Teilkörper; insbesondere kann er so auch zu einem Integritätsring erweitert
werden, indem der Quotientenkörper gebildet und
zu
adjungiert wird. Das heißt
ist der kleinste Integritätsring, der
enthält.
Insbesondere erfüllt jeder Integritätsring die geforderten Eigenschaften; allerdings ist ein Einselement, das der Integritätsring zusätzlich fordert, nicht notwendig, um den Quotientenkörper bilden zu können. Dennoch fordern viele Autoren wegen besserer Übersichtlichkeit einen Integritätsring.
Eigenschaften
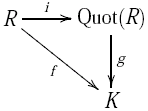
- Der Quotientenkörper eines Körpers ist bis auf Isomorphie der Körper selbst.
- Abstrakt definiert man den Quotientenkörper eines Ringes
durch folgende universelle Eigenschaft: Ein Quotientenkörper ist ein Paar
, wobei
ein Körper und
ein injektiver Ringhomomorphismus ist, mit der Eigenschaft, dass es für jedes Paar
, wobei
ein Körper und
ein injektiver Ringhomomorphismus ist, einen injektiven Körperhomomorphismus
gibt mit
. Anschaulich bedeutet dies, dass man in jeden Körper, in den man
einbetten kann, ebenfalls den Quotientenkörper von
einbetten kann (wobei letztere Einbettung eine Fortsetzung der ersten ist).
Aus der letztgenannten Eigenschaft folgt, dass
der kleinste Körper ist, der
enthält, und dass dieser bis auf Isomorphie eindeutig bestimmt ist, also ist es
gerechtfertigt, von dem Quotientenkörper zu sprechen.
Konstruktion
Man kann den Quotientenkörper
eines Rings
wie folgt konstruieren:
- Erkläre auf
die Äquivalenzrelation
.
- Üblicherweise schreibt man
für die Äquivalenzklasse von
.
- Man setzt nun
gleich der Menge der Äquivalenzklassen:
.
- Definiere auf
die Addition und Multiplikation wie folgt vertreterweise:
- Insbesondere sind die so definierten Operationen wohldefiniert, also die beiden Seiten von der Wahl der Vertreter unabhängig.
- Der Ring ist nicht der Nullring, enthält also ein Element
. Das neutrale Element bezüglich der Addition (das Nullelement) ist
, das neutrale Element bezüglich der Multiplikation (das Einselement) ist
. Diese Äquivalenzklassen sind für alle
gleich. Im Falle des Integritätsrings wird meist
gewählt.
- Für
ist das Inverse bezüglich der Addition durch
gegeben, und falls
ist, ist
invertierbar bezüglich der Multiplikation, wobei das Inverse durch
gegeben ist.
- Damit ist
ein Körper, insbesondere ist für einen Integritätsring
,
ein injektiver Ringhomomorphismus, welcher die gewünschte Einbettung vermittelt. Es gilt
.
Für die Wohldefiniertheit der Struktur von
ist die Kürzungsregel in nullteilerfreien Ringen entscheidend, d.h. dass
für
aus
stets
folgt.
Beispiele
- Der Quotientenkörper
des Integritätsrings
der ganzen Zahlen ist der Körper
der rationalen Zahlen.
- Der Quotientenkörper
des Rings der geraden ganzen Zahlen (ein Ring ohne Eins) ist ebenfalls der Körper
.
- Der Quotientenkörper
des Polynomrings wird häufig als der rationale Funktionenkörper
definiert.
- Der Quadratische
Zahlkörper
ist der Quotientenkörper der Gaußschen Zahlen
- Sei
der Integritätsring der ganzen Funktionen und
der Körper der auf
meromorphen Funktionen. Mit dem Weierstraßschen Produktsatz sieht man, dass man jede auf
meromorphe Funktion als Quotient zweier ganzer Funktionen schreiben kann, folglich ist
.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 16.08. 2022