Satz von Pick

Gitterpolygon

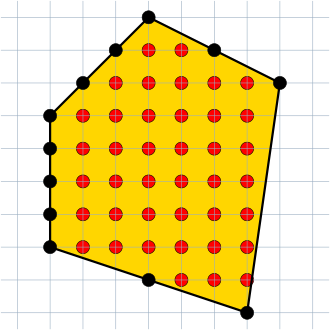
Der Satz von Pick, benannt nach dem österreichischen Mathematiker Georg Alexander Pick, beschreibt eine fundamentale Eigenschaft von einfachen Gitterpolygonen. Dies sind Vielecke, deren sämtliche Eckpunkte ganzzahlige Koordinaten haben. (Man denke sich ein Vieleck, welches auf Rechenpapier gemalt wird, mit den Eckpunkten nur in den Schnittpunkten des Gitters.)

Aussage des Satzes

Sei der Flächeninhalt des Polygons, die Anzahl der Gitterpunkte im Inneren des Polygons und die Anzahl der Gitterpunkte auf dem Rand des Polygons, dann gilt:

$A = I + \frac R 2 - 1$

In dem nebenstehenden Beispiel ist R = 12 und I = 40 . Die Fläche dieses Polygons beträgt somit $\textstyle 40+{\frac {12}{2}}-1=45$ Gitterquadrateinheiten.

Der Satz von Pick kann dazu benutzt werden, um die eulersche Polyederformel zu beweisen und umgekehrt folgt der Satz von Pick aus der Eulerschen Polyederformel, so dass beide Sätze äquivalent sind.

Betrachtet man nicht nur einfache Polygone, sondern auch solche mit „Löchern“, so muss in obiger Formel der Summand „“ durch „ $-\chi(P)$ “ ersetzt werden, wobei $\chi(P)$ die Euler-Charakteristik des Polygons ist. Man erhält somit:

$A=I+{\frac {R}{2}}-\chi (P)$

Beweisidee

Das Theorem ist additiv: Wenn man zwei Polygone mit ganzzahligen Ecken, die sich in einer gemeinsamen Strecke schneiden, zu einem Polygon mit ganzzahligen Eckpunkten verschmilzt, dann addieren sich die realen Flächen und auch die Flächen nach der Formel in dem Satz. Denn die Randpunkte im Innern der Strecke werden zu inneren Punkten, und die Endpunkte der Strecke werden zu zwei Randpunkten.
Der Satz lässt sich für achsenparallele Rechtecke unmittelbar verifizieren.
Wegen der Additivität gilt der Satz dann auch für rechtwinklige Dreiecke mit achsenparallelen Katheten, da es sich hier um halbe Rechtecke handelt.
Ebenso gilt er für Trapeze mit drei achsparallelen Seiten (rechtwinkliges Dreieck plus Rechteck). Betrachtet man zu jeder Seite des gegebenen Polygons das Trapez, das von dieser Seite, zwei vertikalen Linien durch die Endpunkte und einer fernen, aber fest gewählten horizontalen Geraden begrenzt wird, so ist die gegebene Fläche als vorzeichenbehaftete Summe dieser Trapeze darstellbar. Aus der Additivität folgt dann die Behauptung.
Alternativ zum letzten Schritt kann man auch nachweisen, dass der Satz für beliebige Dreiecke gilt, indem man sie durch rechtwinklige Dreiecke zu einem achsenparallelen Rechteck ergänzt. Anschließend folgt der Satz durch Induktion, da man jedes einfache Polygon mit mehr als drei Ecken durch eine ganz im Inneren des Polygons verlaufende Diagonale in zwei einfache Polygone mit weniger Ecken zerlegen kann.

Folgerungen

Eine Folge des Satzes von Pick ist, dass ein ebenes Dreieck mit ganzzahligen Eckpunkten, das außer diesen Eckpunkten keine ganzzahligen Punkte enthält, die Fläche ${\tfrac 12}$ hat. Sind ABC und $A'\!B'\!C'$ zwei solche Dreiecke, so bildet die affine Abbildung, die ABC in $A'\!B'\!C'$ überführt, das Gitter (gemeint sind hier nur die Gitterpunkte) auf sich selbst ab.

Verallgemeinerung

Der Satz von Pick wird durch Ehrhart-Polynome auf drei und mehr Dimensionen verallgemeinert. Vereinfacht ausgedrückt: Für ein -dimensionales Polytop des Volumens betrachtet man eine um einen Faktor skalierte Kopie $k\cdot P$ ; für große überdeckt $k\cdot P$ in erster Näherung $k^{d}\cdot V$ Gitterpunkte.

Eine einfache Formel, die die Anzahl der ganzzahligen Punkte eines höherdimensionalen Polytops mit dessen Volumen verbindet, ist nicht greifbar. So besitzen etwa im dreidimensionalen Fall die Simplizes, die von den vier Punkten (0,0,0) , $(1,0,0)$ , $(0,1,0)$ und $(1,1,r)$ aufgespannt werden, jeweils das Volumen ${\tfrac {r}{6}}$ , enthalten aber außer den Eckpunkten keinen weiteren ganzzahligen Punkt.

Literatur

Georg Alexander Pick: Geometrisches zur Zahlenlehre. (Bearbeitung eines in der deutschen mathematischen Gesellschaft zu Prag gehaltenen Vortrags.) In: Sitzungsberichte des deutschen naturwissenschaftlich-medizinischen Vereines für Böhmen „Lotos“ in Prag 19 (1899), S. 311–319.

Basierend auf einem Artikel in:

Wikipedia.de