
Eulerscher Polyedersatz
Der Eulersche Polyedersatz (auch: Eulersche Polyederformel), benannt nach Leonhard Euler, beschreibt eine fundamentale Eigenschaft von beschränkten, konvexen Polyedern und allgemeiner von planaren Graphen.
Hinter der Formel steckt das topologische Konzept der Euler-Poincaré-Charakteristik
und die Eulersche Polyederformel ist der Spezialfall
,
sie gilt also allgemein für Polyeder der Charakteristik 2, zu denen die konvexen
Polyeder zählen (aber auch einige nicht-konvexe[1]).
Allgemein
Der Satz besagt: Seien
die Anzahl der Ecken,
die Anzahl der Flächen
und
die Anzahl der Kanten eines beschränkten, konvexen Polyeders, dann gilt:
In Worten: Anzahl der Ecken plus Anzahl der Flächen minus Anzahl der Kanten gleich zwei.
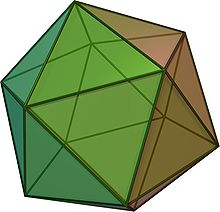
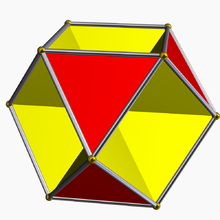
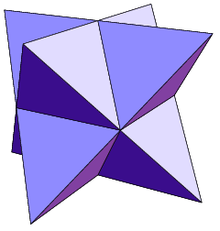
Beispielhaft sind in der folgenden Tabelle die fünf platonischen
Körper mit den zugehörigen Werten für ,
und
aufgeführt. Der eulersche Polyedersatz gilt aber nicht nur für regelmäßige,
sondern für alle beschränkten konvexen Polyeder. Aus dem Satz lässt sich
herleiten, dass es nicht mehr als fünf platonische Körper geben kann.
| Polyeder | E | F | K | |
|---|---|---|---|---|
| Tetraeder | 4 | 4 | 6 | 2 |
| Würfel | 8 | 6 | 12 | 2 |
| Oktaeder | 6 | 8 | 12 | 2 |
| Dodekaeder | 20 | 12 | 30 | 2 |
| Ikosaeder | 12 | 20 | 30 | 2 |
Geschichte
Euler erwähnte den Satz zuerst in einem Brief an Christian Goldbach 1750 und veröffentlichte 1758 einen Beweis,[2] allerdings enthielt er nach den heutigen Maßstäben für die Strenge mathematischer Beweise einen Fehler, worauf Henri Lebesgue 1924 hinwies. Später wurde bekannt, dass der Satz schon René Descartes bekannt war (unveröffentlicht),[3] weshalb er in der französischen Literatur auch als Satz von Descartes und Euler bekannt ist. Der Beweis von Euler benutzt die Zerlegung eines Polyeders in Tetraeder, wobei eine Ecke nach der anderen beseitigt wird. Der erste strenge Beweis wurde von Adrien-Marie Legendre 1794 veröffentlicht, in seinem Buch Élements de Géométrie. Legendres Beweis benutzt die Flächenformel eines geodätischen Dreiecks auf der Kugeloberfläche. Einen korrekten Beweis fand auch Augustin Louis Cauchy 1811, veröffentlicht 1813. Bis heute sind viele verschiedene Beweise bekannt.
Eine Verallgemeinerung auf n-dimensionale Polyeder fanden Ludwig Schläfli und Henri Poincaré (1895). Poincaré erkannte auch die volle topologische Bedeutung des Satzes.
Verallgemeinerung auf planare Graphen
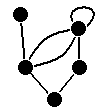
Vom Polyeder zum planaren Graphen
Hat ein Polyeder ein zusammenhängendes Inneres ohne Löcher, kann die Beziehung seiner Flächen, Kanten und Ecken auch als planarer Graph (ein ebenes, zusammenhängendes Netz, dessen Kanten einander nicht schneiden) dargestellt werden.
Dies kann man sich wie folgt veranschaulichen: Entfernt man eine Fläche des Polyeders und zieht die angrenzenden Kanten auseinander, kann man das Netz des Polyeders auf eine Ebene projizieren und in einen planaren Graphen überführen. Dabei bleiben nicht unbedingt alle Regelmäßigkeiten des Polyeders erhalten – die entstehenden Flächen müssen noch nicht einmal Vielecke sein –, die Anzahl der Ecken, Kanten und Flächen (die Außenfläche mitgezählt) sowie die Struktur des Netzes bleiben aber erhalten.
Der eulersche Polyedersatz für planare Graphen
Für zusammenhängende planare Graphen kann eine verallgemeinerte Version des eulerschen Polyedersatzes formuliert werden. Dort ersetzen die Gebiete die Flächen und es gilt
- Knotenzahl + Gebietszahl − Kantenzahl = 2,
wobei bei der Gebietszahl das äußere Gebiet mitgezählt wird.
Diese Formulierung erweitert den Gültigkeitsbereich des Satzes um eine Vielzahl nicht-konvexer Polyeder sowie solche planaren Graphen, denen überhaupt keine Polyeder zugrunde liegen.
Wird der eulersche Polyedersatz zuerst für planare Graphen bewiesen, so ergibt sich der klassische Polyedersatz hieraus als Spezialfall.
Die Euler-Charakteristik
Eine weiterreichende Verallgemeinerung des Konzepts findet sich in der Euler-Charakteristik einer geschlossenen Fläche. Aus dieser Sichtweise ist die Konvexität des Polyeders lediglich eine (starke) hinreichende Voraussetzung, um zu gewährleisten, dass die Oberfläche des Polyeders homöomorph zur 2-Sphäre ist.
Ein klassischer Beweis

Der einfachste Graph |

Entstehung des Würfelnetzes |
Hinzufügen einer Ecke mit
Kante |

Hinzufügen einer
Kante |
Dieser Beweis zeigt mit struktureller Induktion die Gültigkeit des Satzes für planare Graphen.
Der einfachste planare Graph besteht nur aus einer Ecke. Es gibt eine
Fläche (die Außenfläche) und keine Kanten. Es gilt also .
Aus diesem einfachsten Graphen können alle weiteren ausschließlich durch die
beiden folgenden Operationen konstruiert werden, welche die Gültigkeit
des Satzes nicht verändern:
- Hinzufügen einer Ecke, die über eine neue Kante mit dem Rest des
Graphen verbunden ist. Die Anzahl der Ecken und Kanten steigt jeweils um eins,
während die Anzahl der Flächen gleichbleibt. Galt für den alten Graphen
, so gilt es auch für den neuen, da auf der linken Seite der Gleichung je eine Eins addiert und abgezogen wurde.
- Hinzufügen einer Kante, die zwei bereits bestehende Ecken
verbindet. Während die Anzahl der Ecken gleichbleibt, steigt die Anzahl der
Flächen und Kanten jeweils um eins. Wieder bleibt die Summe
gleich, da je eine Eins addiert und abgezogen wurde.
Da der Satz für den ersten, einfachsten Graphen galt, muss er also auch für jeden Graphen gelten, der durch eine der beiden Operationen aus diesem entsteht. Jeder Graph, der durch eine weitere Operation aus einem solchen Graphen entsteht, muss den Satz ebenfalls erfüllen usw. Daher gilt der Satz für alle planaren Graphen und damit auch für alle konvexen Polyeder.
Der Beweis stammt von Cauchy. Er war der Erste, der das Problem auf ein solches der Graphentheorie reduzierte.
Ein ungewöhnlicher Beweis
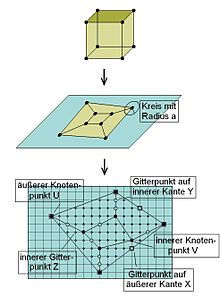
Dieser Beweis zeigt die Gültigkeit des Satzes für planare Graphen mit Hilfe des Satzes von Pick.
Um den Satz von Pick anwenden zu können, muss der Graph in ein Gitternetz
eingebettet werden, so dass die Knotenpunkte des Graphen auf Gitterpunkten
liegen. Der Graph bleibt äquivalent, wenn man jeden Knotenpunkt innerhalb einer
geeignet kleinen Umgebung bewegt. Der Radius des kleinsten Kreises um einen
Knotenpunkt, der vollständig in die Umgebung eingebettet ist, sei .
Es wird ein beliebiges Gitternetz mit Einheit
auf der Ebene betrachtet. Dann können wir jeden Knotenpunkt auf einen
Gitterpunkt verschieben und erhalten sicher einen äquivalenten Graphen. Der
planare Graph besitzt jetzt insgesamt
Knotenpunkte,
Kanten und
innere Flächen.
Die gesamte (innere) Fläche
des planaren Graphen kann mit Hilfe des Satzes
von Pick auf zwei Arten bestimmt werden. Zunächst müssen alle Gitterpunkte
innerhalb oder auf dem Graphen charakterisiert werden. Die Punkte innerhalb
werden in drei Kategorien eingeteilt: Knotenpunkte
,
Punkte auf Kanten
und sonstige
,
die Punkte auf dem Rand in: Knotenpunkte
und Punkte auf Kanten
.
Die Anzahl der Punkte
sei
.
Offensichtlich gilt dann für die Zahl der Ecken bzw. Knoten
.
(i) Betrachten wir den Graphen ohne seine genaue innere Struktur: Es gibt
dann insgesamt
Gitterpunkte im Inneren und
Punkte auf dem Rand. Nach dem Satz von Pick gilt für die Fläche des Graphen:
(ii) Die Fläche
lässt sich auch berechnen, indem man die Flächen der
inneren Gebiete des Graphen mit Hilfe des Satzes von Pick aufsummiert. Die Summe
aller inneren Punkte ist dann natürlich
.
Die Gitterpunkte auf den Kanten und die Knotenpunkte des Graphen liegen auf
einem oder mehreren Rändern der
-Gebiete
und treten daher mehrmals in der Summe über die
-Flächen
auf.
Die Gitterpunkte auf Kanten im Inneren (Punkte Y) gehören zu jeweils zwei Flächen, kommen also in der Summe zweimal vor. Die Gitterpunkte auf Kanten am Rand (Punkte X) treten nur einmal auf.
Betrachten wir nun die inneren Knotenpunkte .
Sie grenzen an ebenso viele innere Gebiete, wie Kanten von ihnen wegführen. Bei
den Knotenpunkte am Rand
gibt es eine Kante mehr als benachbarte innere Flächen. Addiert man nun die Zahl
der wegführenden Kanten über alle Knoten, so erhält man
,
da jede Kante doppelt vorkommt. Addiert man die Zahl der benachbarten inneren
Flächen über alle Knoten, so erhält man
,
da die Zahl der wegführenden Kanten der Zahl der benachbarten Flächen entspricht
bis auf eine 1 bei den
Knotenpunkten am Rand. Die Knotenpunkte treten also in der Summe über alle
-Flächen
insgesamt
-mal
auf.
Für die Fläche des Graphen gilt also mit -maliger
Anwendung des Satzes von Pick:
Durch Gleichsetzen der beiden Flächenformeln (i) und (ii) fallen die Terme
mit
heraus, und man erhält mit
direkt die eulersche Polyederformel:
Beweis nach von Staudt
Karl von Staudt gab 1847 einen einfachen, nicht-rekursiven Beweis in seiner Geometrie der Lage.
Dazu betrachte man den Graphen
der planaren Projektion des Polyeders, das
Knoten,
Kanten und
Flächen hat. Der Graph ist für die betrachteten Polyeder zusammenhängend[4]
und hat damit einen Spannbaum
.
Da
genau
Knoten enthält und ein zusammenhängender Baum ist (ohne Zykel), hat er
Kanten. Man betrachte nun den zu
dualen Graphen
,
gebildet aus den Mittelpunkten der Flächen von
,
und verbinde diese so mit Kanten, dass diese die Kanten in
nicht schneiden. Dieser Kantenzug
ist zusammenhängend, da
keine Kreise enthält. Er ist ebenfalls ein Baum, sonst würde er einen Kreis
(Zykel) enthalten, der die Knoten von
in zwei Teile teilt und somit eine Kante von
schneidet, entgegen der Konstruktionsvoraussetzung.
hat damit
Knoten und
Kanten. Die Kanten in
setzen sich aus den Kanten von
zusammen oder werden von einer Kante von
gekreuzt, somit gilt:
.
Anmerkungen
- ↑ Darauf wies zuerst Louis Poinsot 1810 hin
- ↑ Euler: Elementa doctrine solidorum. In: Novi comm. acad. scientiarum imperialis petropolitanae, 4, 1758, S. 72–93 (Eneström Index E 230). Euler: Demonstratio nonnullarum insignium proprietatum quibus solida hedris planis inclusa sunt praedita. In: Novi Commentarii Academiae Scientiarum Petropolitanae, 4, 1758, S. 94–108 (sein Beweis, E 231). Nachdruck in Opera Omnia, Band 26. Die beiden Arbeiten stammen schon von 1750 bzw. 1751.
- ↑ E. de Jonquières: Note sur une pointe fundamental de la théorie des polyèdres. In: Comptes Rendus Acad. Sci., Paris, 110, 1890, S. 110–115. Aus Descartes nachgelassenen Schriften, überliefert nur aus einer Kopie von Gottfried Wilhelm Leibniz, 1860 in der Landesbibliothek Hannover entdeckt. Richeson: The polyhedral formula.
- ↑ Historisch leitete Staudt damit ein Kriterium für die Polyeder ab, für die der Satz zutrifft


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.02. 2026