Hamel-Oseenscher-Wirbel
Der Hamel-Oseen’sche oder Lamb-Oseen’sche Wirbel (von Carl Wilhelm Oseen, Georg Hamel, Horace Lamb, im Folgenden einfach Oseen’scher Wirbel) ist ein mathematisches Modell einer Wirbelströmung eines linear viskosen, inkompressiblen Fluids. Das Geschwindigkeitsfeld von Strömungen solcher Fluide wird in der Strömungsmechanik mit den Navier-Stokes-Gleichungen beschrieben, die vom Oseen’schen Wirbel exakt erfüllt werden. Das Fluid strömt rein kreisförmig jedoch zeitabhängig, instationär um das Wirbelzentrum. Die Viskosität zehrt die kinetische Energie des Wirbels vor allem in der sich ausbreitenden Zentralregion des Wirbels mit der Zeit auf und die Strömungsgeschwindigkeit nimmt monoton mit der Zeit ab.
Zu Beginn der Bewegung oder im Grenzfall verschwindender Viskosität ist der Wirbel ein Potentialwirbel. Ansonsten ist das Geschwindigkeitsprofil des Oseen’schen Wirbels beschränkt und entspricht im Wirbelzentrum, sowie im Außenbereich einem Rankine Wirbel.
Umfangsgeschwindigkeit


Im Oseen’schen Wirbel bewegen sich die Fluidelemente in der Wirbelebene
kreisförmig um das Wirbelzentrum. Die beiden Abbildungen rechts geben einen
Eindruck der Geschwindigkeitsverteilung als Funktion des Abstandes vom Zentrum.
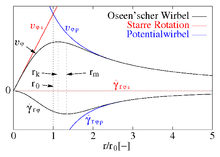
Das obere Bild zeigt die Geschwindigkeitsverteilung zu verschiedenen Zeiten als
Funktion des Radius (
s. u.). Die schwarz gepunktete Kurve („vmax“) verbindet die Punkte mit maximaler
Umfangsgeschwindigkeit, die den Kernradius markieren. Die
Umfangsgeschwindigkeit nimmt zeitlich besonders innerhalb des doppelten
Kernradius ab. Vor allem innerhalb dieser Kernregion, die sich mit der Zeit
ausdehnt, wird kinetische Energie dissipiert.
Außerhalb des Kernradius geht der Oseen’sche Wirbel in den stationären
Potentialwirbel reibungsfreier Fluide über (schwarze Kurve im Bild), wo keine
Dissipation stattfindet. Bei doppeltem Kernradius ist die
Geschwindigkeitsabweichung vom Potentialwirbel bereits auf 2 % geschrumpft.
Für die mathematische Beschreibung des Oseen’schen Wirbels wird ein Zylinderkoordinatensystem benutzt. Die Strömung ist dann nur von der radialen Koordinate r und der Zeit t abhängig und besitzt die Umfangsgeschwindigkeit:
Der Materialparameter ν ist die kinematische
Viskosität (Dimension
L2T−1, Luft 14 mm²/s, Wasser 1 mm²/s),
ein mit derselben Dimension versehener Parameter, der die
Strömungsgeschwindigkeit kontrolliert, der Nenner
ist der Kernradius des Rankine-Wirbels,
der sich zu einer gegebenen Zeit t an den Oseen’schen Wirbel anschmiegt, und
ex bezeichnet die e-Funktion.
Die Geschwindigkeitsverteilungen der starren Rotation, des Potentialwirbels –
was beides zusammen den Rankine-Wirbel ergibt – und des Oseen’schen Wirbels sind
in der unteren Abbildung rechts für den Fall
dargestellt.
Der Kernradius eines Wirbels ist derjenige Radius, bei dem das Geschwindigkeitsmaximum auftritt. Im Geschwindigkeitsmaximum muss zu einer bestimmten Zeit t die Ableitung
verschwinden, was bei
näherungsweise der Fall ist. Die maximale Geschwindigkeit
tritt im Radius
auf. Dies ist der Kernradius des Oseen’schen Wirbels. Die Grenzwerte
existieren und daher nimmt zu einer bestimmten Zeit im Zentrum des Wirbels
linear mit dem Radius zu:
Die Geschwindigkeitsverteilung
entspricht einer starren Rotation. In einem größeren Abstand vom Zentrum (
)
ist die Umfangsgeschwindigkeit etwa die des Potentialwirbels:
An der Stelle
sind die Umfangsgeschwindigkeiten der starren Rotation und des Potentialwirbels
gleich und diese Stelle ist – wie oben gesagt – der Kernradius des
Rankine-Wirbels. Unter Berücksichtigung der Einheiten ergibt sich bei einem
Kernradius
und einer Zirkulation
eine maximale Umfangsgeschwindigkeit
,
so dass die Fluidelemente das Zentrum einmal pro Sekunde umrunden. Im Abstand
von 50 Zentimetern wäre die Umfangsgeschwindigkeit bereits auf
abgesunken, so dass Fluidelemente in diesem Abstand das Zentrum nur alle sieben
Sekunden einmal umrunden.
Wirbelstärke

Die Wirbelstärke in einer ebenen Strömung ist das Doppelte der Winkelgeschwindigkeit der Fluidelemente um sich selbst. Bei einer ebenen Strömung hat die Wirbelstärke nur eine Komponente senkrecht zur Ebene und somit kann sie als Skalarfeld behandelt werden. Beim Oseen’schen Wirbel lautet die Wirbelstärke:
Dies ergibt sich aus der Geschwindigkeit
und deren Rotation
in Zylinderkoordinaten:
Für
geht die Wirbelstärke in das Dirac-Delta
über, was zu einem Potentialwirbel passt. Die Ableitung der Wirbelstärke nach dem Radius berechnet sich zu:
Bei
verschwindet diese Ableitung und die Wirbelstärke ist gleich der doppelten
Drehgeschwindigkeit
im Zentrum. Im Zentrum findet also eine starre Rotation statt. Für
geht die Wirbelstärke gegen null, weswegen sich auch hier der Potential- und
Rankine-Wirbel an den Oseen’schen Wirbel anschmiegen.
Druck

Der Druckgradient in einem kreisförmig strömenden Wirbel gleicht gerade die Zentrifugalkraft aus, so dass die Fluidelemente im Kreis strömen, was sich in Zylinderkoordinaten aus den Navier-Stokes-Gleichungen ergibt (siehe unten) und im Oseen’schen Wirbel auf die Bedingung
hinaus läuft. Unter Verwendung der Integralexponentialfunktion Ei mit den Eigenschaften
kann die obige Ableitung geschlossen integriert werden mit dem Ergebnis:
Die Integrationskonstante
ist der Druck im (unendlich) fernen Außenbereich. Im Zentrum herrscht der Druck
| Beweis: |
| Mit den Abkürzungen
Mit dem Grenzwert |
Das Bild zeigt die Druckverteilung bei einem verschwindenden Außendruck. Der
Faktor
ist der Druck im Potentialwirbel, der sich an den Oseen’schen Wirbel anschmiegt
(blaue Kurve):
Wieder deutet der Druck im Zentrum auf eine starre Rotation hin, denn bei
dieser ist die Umfangsgeschwindigkeit
proportional zum Radius
weswegen der Druckverlauf dann über dem Radius parabelförmig ist (rote Kurve im Bild).
Kinetische Energie

Die kinetische Energie des Fluids innerhalb eines vielfachen des Kernradius des Rankine-Wirbels ist weder vom Kernradius noch von der Zeit abhängig solange die Vielfachheit beibehalten wird:
Der Wert in den eckigen Klammern ist mit der Euler-Mascheroni-Konstante
nur eine Funktion des Faktors n, siehe die Abbildung rechts. Die kinetische
Energie des Fluids innerhalb des sich ausweitenden Radius
ist bei festgehaltenem Verhältnis n mithin über die Zeit konstant. Umgekehrt
heißt das: Die kinetische Energie der in einem Zeitintervall von einem Kreis mit
n-fachem Kernradius neu eingenommenen Fluidelemente wird in diesem Zeitintervall
innerhalb des Kreises dissipiert.
| Beweis: |
| Mit der Umfangsgeschwindigkeit
ergibt sich die kinetische Energie des Fluids innerhalb eines
Vielfachen des Rankine-Kernradius zu nur eine Funktion des Faktors n. Mit diesen Ergebnissen berechnet sich
die kinetische Energie – wie angekündigt – zu |
Zirkulation

Ein Maß für die Drehgeschwindigkeit in einem Fluid ist die Zirkulation, die das Kurvenintegral der Geschwindigkeit entlang eines geschlossenen Weges ist. Entlang eines Kreises K mit Radius r berechnet sich:
Der Funktionsverlauf ist im Bild rechts dargestellt ()
In weiter Ferne vom Wirbelzentrum (
)
nähert sich die Zirkulation dem Parameter Γ0 an, der die über den
Radius konstante Zirkulation des Potentialwirbels ist (blaue Linie), der sich an
den Oseen’schen Wirbel außen anschmiegt. Im Abstand des doppelten Kernradius
weicht die Zirkulation nur noch um 2 % vom Parameter
ab. Die Zeitabhängigkeit der Zirkulation widerspricht dem Kelvin’schen
Wirbelsatz für reibungsfreie Fluide und dieser Widerspruch löst sich mit
auf.
Im Zentrum ist die Geschwindigkeit proportional zum Radius und dann lautet die Zirkulation:
Sie ist im Bild rot gezeichnet. Zur Zeit t=0 startet der Wirbel mit der
Zirkulation Γ0, die in einem vorgegebenen Abstand mit
fortschreitender Zeit gegen null geht, weil die Viskosität – vor allem im
Wirbelkern – die kinetische Energie aufzehrt und sich der Kernradius
r0 mit der Zeit ausdehnt. Bei festgehaltenem Verhältnis
ist die Zirkulation über die Zeit konstant, oder – anders ausgedrückt – weiten
sich die Kreise bei festgehaltener Zirkulation wie der Kernradius mit der Zeit
aus.
Schubverzerrungsgeschwindigkeit
Die Schubverzerrungsgeschwindigkeit
im Fluid ergibt sich gemäß
aus dem Verzerrungsgeschwindigkeitstensor d, der der symmetrische Anteil
des Geschwindigkeitsgradienten
ist. In den hier verwendeten Zylinderkoordinaten berechnet sich der Gradient
zu:[F 1]
Das Superskript
kennzeichnet die Transposition
und das Rechenzeichen „
“
bildet das dyadischen
Produkt. Bei der starren Rotation tritt keine Schubverzerrung auf
und der in obiger Formel unterstrichene Term ist die
Schubverzerrungsgeschwindigkeit
im Potentialwirbel, siehe Bild.
Die maximale Schubverzerrungsgeschwindigkeit tritt dort auf, wo ihre Steigung null ist:
Das ist bei
näherungsweise der Fall. Die maximale Schubverzerrungsgeschwindigkeit zeigt sich
also beim etwa 1,2-fachen des Kernradius
- Bemerkung
- Der schiefsymmetrische Anteil des Geschwindigkeitsgradienten ist der Wirbeltensor.
- dessen dualer Vektor
– definiert über
– die Winkelgeschwindigkeit oder die halbe Wirbelstärke ist:
Zeitverläufe

In den vorangegangenen Abschnitten wurden die Verläufe der Größen zu einer bestimmten Zeit als Funktion des Radius beleuchtet. In diesem Abschnitt soll der Zeitverlauf bei einem bestimmten Radius in den Blick gerückt werden.
Der Kernradius dehnt sich mit der Zeit aus. Sei
die Kernzeit, die verstreicht, bis der Rankine-Kernradius auf eine vorgegebene Größe r angewachsen ist. Die Kernzeit nimmt mit dem Quadrat des Radius zu.
Die Geschwindigkeit eines Fluidelementes in einem bestimmten Abstand r vom Zentrum ist
Bis
weicht die Umfangsgeschwindigkeit um maximal 2 % von der des
Potentialwirbels ab. Danach nimmt die Geschwindigkeit rasch ab, siehe die rote
Kurve im Bild. Das Verhältnis der Zirkulation zu
hat bei einem gegebenen Radius denselben Zeitverlauf.
Bei einem festen Radius r nimmt die Wirbelstärke zunächst zu und später
wieder ab und durchläuft dazwischen ein Maximum. Anfangs ist die Rotation
geringer, weil sich das Fluidelement etwa wie im rotationsfreien Potentialwirbel
bewegt, dann nimmt sie auf Grund von Reibeffekten zu und später, wenn das
Fluidelement innerhalb des Kernradius ist, nimmt die Wirbelstärke wegen der
Aufzehrung der kinetischen Energie wieder ab. Im Maximum verschwindet die
Zeitableitung
der Wirbelstärke:
Die Wirbelstärke kann mit der Kernzeit ausgedrückt werden und so ihr Maximum dargestellt werden:
Das Verhältnis der Wirbelstärke zu ihrem Maximum bei gegebenem Radius r (grüne Kurve im Bild) ist demnach:
Bei
wenn das Fluidelement auf dem Rankine-Kernradius liegt, rotiert es am
schnellsten um sich selbst.
Der Druck-Zeit-Verlauf (blaue Kurve im Bild) ergibt sich aus
Für
folgt aus der Reihenentwicklung der Integralexponentialfunktion
Daher geht die Druckdifferenz
mit der Zeit gegen null.
Die Schubverzerrungsgeschwindigkeit über die Zeit (orange Kurve im Bild) ergibt sich zu:
Navier-Stokes-Gleichungen
Dass die Modellgleichungen des Oseen’schen Wirbels die
Navier-Stokes-Gleichungen erfüllen, lässt sich an den Gleichungen für ein
dichtebeständiges Fluid ohne Schwerefeld in Zylinderkoordinaten nachweisen.
Unter diesen Umständen lauten die Navier-Stokes-Gleichungen, wenn alle Variablen
nur vom Radius oder der Zeit abhängen und die Bewegung rein kreisend ist ():
Aus der ersten Gleichung berechnete sich oben der Druck. Die zweite Gleichung wird mit dem angegebenen Geschwindigkeitsfeld
erfüllt, was mit
nachgewiesen werden kann.
In Zylinderkoordinaten ergibt sich aus
die Divergenzfreiheit
der Wirbelströmung, die über die Massenbilanz
eine zeitlich konstante Dichte bedingt, die wiederum im Einklang mit der
Inkompressibilität des Fluids ist.
Siehe auch
Fußnoten
- ↑
In Zylinderkoordinaten berechnet sich der
Gradient eines Vektorfeldes gemäß
und der Gradient eines Skalarfeldes mit
Literatur
- F. Kameier, C. O. Paschereit: Strömungslehre. Walter de Gruyter, 2013, ISBN 978-3-11-018972-8.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 17.04. 2021