Wirbelstärke

Die Wirbelstärke ${\vec {\omega }}$ bzw. ${\vec {\eta }}$ bzw. ${\vec {\zeta }}$ beziffert eine zentrale Größe der Strömungsmechanik und der Meteorologie, indem sie dem Strudel und den kreis- oder spiralförmigen Strömungen ein Feld von Geschwindigkeiten zuordnet. Die gleichwertige Bezeichnung Vortizität von lateinisch vortex = „Wirbel, Strudel“, englisch Vorticity, wird mit Wirbelhaftigkeit übersetzt.

In der Strömungsmechanik werden kleine Unterschiede in Geschwindigkeit und Richtung von Gasen und Flüssigkeiten als Scherung bezeichnet. Die Stromlinien sind anderseits geometrische Hilfsmittel zur anschaulichen Beschreibung einer Strömung als gerichtete Bewegung von Teilchen. Schließlich ist die Viskosität die Zähflüssigkeit oder Zähigkeit von Fluiden, also der Widerstand des Fluids gegenüber Scherung.

Anschaulich entspricht die Wirbelstärke der Tendenz eines Fluidelements zur Eigendrehung um eine Achse, aus der eine Zirkulation von fließenden oder strömenden Medien in einem geschlossenen Gebiet entsteht. Weiter wird das Mittel der quadratischen Wirbelstärke über einer bestimmten Fläche als Enstrophie bezeichnet, welche z.B. das Strömungsverhalten von Glas-Doppelfassaden beschreibt.

Formale Notation

Die Wirbelstärke ${\vec {\omega }}$ , in der Meteorologie angelehnt an die Zirkulation mit ${\vec {\zeta }}$ bezeichnet, ist definiert als die Rotation der Geschwindigkeit ${\vec {u}}$ eines Vektorfelds:

${\vec {\omega }}:=\operatorname {rot} {\vec {u}}={\vec {\nabla }}\times {\vec {u}}$

Sie hat die SI-Einheit ${\tfrac {1}{\mathrm {s} }}$ und ist wie jede Rotation eines Vektorfelds ein Pseudovektorfeld.

Weil sich einem abgeschlossenen System die Erhaltungsgrößen nicht ändern, ist die Wirbelstärke gleich der flächenbezogenen Zirkulationsrate $\Gamma$ :

$\Gamma :=\oint _{\partial A}{\vec {v}}\cdot \mathrm {d} {\vec {r}}=\int _{A}\;\operatorname {rot} ({\vec {v}})\cdot \mathrm {d} {\vec {A}}$

$\Rightarrow {\vec {\omega }}\cdot {\vec {n}}={\frac {\mathrm {d} \Gamma }{\mathrm {d} A}}$

mit der Normalen ${\vec {n}}$ .

In der Meteorologie liegen – außer bei echt dreidimensionalen Wirbeln wie Tornados – oft zweidimensionale Geschwindigkeitsfelder vor. Die entsprechende Vortizität zeigt in z-Richtung und lautet

${\vec {\zeta }}:=\operatorname {rot} {\vec {u}}_{2D}=\left({\frac {\partial u_{y}}{\partial x}}-{\frac {\partial u_{x}}{\partial y}}\right){\vec {e}}_{z}$ .

Hydrodynamik

In der Hydrodynamik ist die Vortizität die Rotation der Fluidgeschwindigkeit, die in Richtung der Rotationsachse bzw. für zweidimensionale Flüsse senkrecht zur Flussebene orientiert ist. Für Fluide mit einer festen Rotation um eine Achse (z.B. einen rotierenden Zylinder) ist die Wirbelstärke gleich der doppelten Winkelgeschwindigkeit ω₀ des Fluidelements:

${\vec {\omega }}=2{\vec {\omega }}_{0}$

${\vec {\omega }}={\vec {\nabla }}\times {\vec {u}}={\vec {\nabla }}\times \left({\vec {\omega }}_{0}\times {\vec {r}}\right)={\vec {\omega }}_{0}\left({\vec {\nabla }}\cdot {\vec {r}}\right)-\left({\vec {\omega }}_{0}\cdot {\vec {\nabla }}\right){\vec {r}}=3{\vec {\omega }}_{0}-{\vec {\omega }}_{0}=2{\vec {\omega }}_{0}$

Fluide ohne Wirbelstärke heißen rotations- oder wirbelfrei mit ${\vec {\omega }}=0\;{\text{bzw.}}\;\zeta =0$ . Allerdings können auch die Fluidelemente eines solchen rotationsfreien Fluids eine Winkelgeschwindigkeit ${\vec {\omega }}_{0}\neq 0$ besitzen, d.h. sich auf gekrümmten Bahnen bewegen, vgl. die folgende Abbildung, wobei der Buchstabe $\omega$ im Text für die Wirbelstärke und in der Abbildung für die Winkelgeschwindigkeit steht:

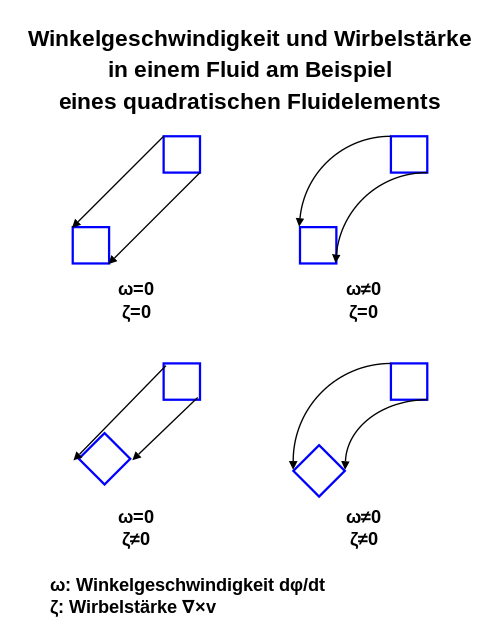
Vortizität und Winkelgeschwindigkeit

Man betrachtet ein infinitesimal kleines, quadratisches Gebiet einer Flüssigkeit. Wenn dieses Gebiet rotiert, ist die Wirbelstärke der Strömung ungleich null. Die Wirbelstärke bezieht sich auf erzwungene Wirbel mit ${\vec {\omega }}=\operatorname {rot} {\vec {u}}\neq 0$ .

Die Vortizität ist ein geeignetes Mittel für Flüssigkeiten mit kleiner Viskosität. Dann kann die Vortizität an fast allen Orten der Strömung als gleich null angesehen werden. Dies ist offensichtlich für zweidimensionale Strömungen, in denen der Fluss auf der komplexen Ebene dargestellt werden kann. Derartige Probleme können meist analytisch gelöst werden.

Für jede Strömung können die bestimmenden Gleichungen durch einfaches Ersetzen auf die Wirbelstärke anstatt auf die Geschwindigkeit bezogen werden. Dies führt zur Wirbeldichtegleichung, die für inkompressible, nichtviskose Flüssigkeiten wie folgt lautet:

${\frac {\mathrm {D} {\vec {\omega }}}{\mathrm {D} t}}=({\vec {\omega }}\cdot {\vec {\nabla }}){\vec {u}}$

Auch für reale Strömungen (dreidimensional, endliche Reynoldszahl, d.h. Viskosität ungleich Null) ist die Betrachtung des Flusses über die Wirbelstärke mit Einschränkungen nutzbar, wenn man annimmt, dass das Vortizitätsfeld als eine Anordnung einzelner Wirbel darstellbar ist. Die Diffusion dieser Wirbel durch die Strömung wird durch die Wirbeltransportgleichung beschrieben:

${\frac {\mathrm {D} {\vec {\omega }}}{\mathrm {D} t}}=({\vec {\omega }}\cdot {\vec {\nabla }}){\vec {u}}+{\frac {\eta }{\rho }}\cdot (\nabla ^{2}{\vec {\omega }})$

wobei $\nabla ^{2}$ den Laplace-Operator bezeichnet. Hier wurde die Wirbeldichtegleichung durch den Diffusionsterm ${\frac {\eta }{\rho }}\cdot (\nabla ^{2}{\vec {\omega }})$ ergänzt.

Für hochviskose Strömungen, beispielsweise Couette-Strömungen, kann es sinnvoller sein, direkt das Geschwindigkeitsfeld des Fluids anstelle der Wirbelstärke zu betrachten, da die hohe Viskosität zu einer sehr starken Diffusion der Wirbel führt.

Die Wirbellinie hängt direkt mit der Wirbelstärke zusammen, indem Wirbellinien Tangenten an die Wirbelstärke sind. Die Gesamtheit der durch ein Flächenelement gehenden Wirbellinien wird als Wirbelfaden bezeichnet. Die Helmholtzschen Wirbelsätze sagen aus, dass der Wirbelfluss $\iint {\vec {\omega }}\cdot \mathrm {d} {\vec {A}}$ sowohl zeitlich als auch räumlich konstant ist.

Meteorologie

In der Meteorologie wird mit der Vortizität hauptsächlich die Rotation von Luft um eine Achse beschrieben.

Die absolute Vortizität $\omega _{\mathrm {abs} }$ eines Volumenelements oder eines Körpers in der Meteorologie setzt sich zusammen aus zwei Summanden, der planetaren Vortizität $f_{{\mathrm {c}}}$ und der relativen Vortizität $\omega _{\mathrm {rel} }$ bzw. $\zeta$ :

${\begin{aligned}\omega _{\mathrm {abs} }=\colon \eta &=f_{\mathrm {c} }+\omega _{\mathrm {rel} }\\&=f_{\mathrm {c} }+\zeta \end{aligned}}$

Aufgrund der Erddrehung $\omega _{0}$ erfährt jeder Körper in Erdnähe eine Rotation um die Erdachse und besitzt somit eine feste Vortizität. Diese wird bestimmt durch den Coriolisfaktor

$f_{\mathrm {c} }=2\omega _{0}\sin \varphi \approx 10^{-4}\,{\frac {1}{\mathrm {s} }}$ ,

der vom Breitengrad $\varphi$ abhängt, und als planetare Vortizität bezeichnet.

Die relative Vortizität ist die mit der Eigendrehung des Körpers zusammenhängende Größe. Da in der Meteorologie meist zweidimensionale Strömungsfelder auftreten, wird sie oft durch die Rotation in zwei Dimensionen ausgedrückt:

${\vec {\zeta }}:=\operatorname {rot} {\vec {u}}_{2D}$

Die Richtung des Wirbelstärke-Vektors lässt sich mit der Korkenzieherregel bestimmen: Dreht sich das Fluid gegen den Uhrzeigersinn, so zeigt die Wirbelstärke nach oben und ist positiv. Auf der Nordhalbkugel wird Rotation gegen den Uhrzeigersinn, also mit positivem $\eta$ , als zyklonale Rotation bezeichnet und mit negativem $\eta$ als antizyklonale Rotation. Auf der Südhalbkugel gilt dies jeweils entsprechend umgekehrt.

In natürlichen Koordinaten ergibt sich:

${\begin{alignedat}{2}\zeta &=\zeta _{C}&&+\zeta _{S}\\&=v\cdot K_{s}&&-{\frac {\partial v}{\partial n}}\end{alignedat}}$

mit

der Krümmungsvortizität
- der Krümmung $K_{s}$ der Stromlinien
der Scherungsvortizität
- den Komponenten n und s des Koordinatensystems.

Potentielle Vortizität

Die Helmholtzschen Erhaltungssätze für den Wirbelfluss führen zur potentiellen Vortizität PV:

$PV={\frac {\eta }{\Delta p}}={\frac {f_{c}+\zeta }{\Delta p}}$

Durch Kombination der Wirbeldichtegleichung mit der Kontinuitätsgleichung kann man zeigen, dass die potentielle Vortizität zeitlich erhalten ist:

${\frac {\mathrm {d} PV}{\mathrm {d} t}}=0$

Anmerkungen

Die Literatur enthält auch die Definition

${\vec {\omega }}={\frac {1}{2}}\operatorname {rot} {\vec {u}}$

Die Begriffe Wirbelstärke, Wirbeldichte, Wirbelhaftigkeit, Wirbeligkeit, Wirbelung, Vortizität, Wirbelfaden sowie die Benennung der Wirbeldichte- und Wirbeltransportgleichung sind nicht klar definiert und somit schwer gegeneinander abgrenzbar. In der Literatur finden sich teilweise widersprüchliche Angaben und Definitionen.

Literatur

Ludwig Bergmann, Clemens Schaefer: Lehrbuch der Experimentalphysik. Band 1: Mechanik, Relativität, Wärme. de Gruyter, Berlin 1998. ISBN 3-11-012870-5
Lew D. Landau, Jewgeni M. Lifschitz: Lehrbuch der theoretischen Physik. Band 6: Hydrodynamik. Verlag Harri Deutsch, Frankfurt am Main 2007. ISBN 978-3-8171-1331-6

Basierend auf einem Artikel in:

Wikipedia.de