Gammakorrektur

Die Gammakorrektur ist eine namentlich im Bereich der Bildverarbeitung häufig verwendete Korrekturfunktion zur Überführung einer physikalisch proportional (d.h. linear) wachsenden Größe in eine dem menschlichen Empfinden gemäß nicht linear wachsende Größe. Mathematisch gesehen handelt es sich bei dieser Funktion um eine Potenzfunktion mit einem oft nur kurz Gamma genannten Exponenten als einzigem Parameter.

Einführung

Übertragungskurven für γ=3, 1, und 0,3.

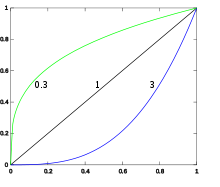
Die Gammakorrektur überführt eine Eingangsgröße I_in gemäß einer Abbildungsvorschrift in eine Ausgangsgröße I_out:

$I_{{{\mathrm {out}}}}={I_{{{\mathrm {in}}}}}^{{\gamma }}$

Dabei gilt:

$0\leq {I_{{{\mathrm {in}}}}}\leq 1$

und

$0\leq {I_{{{\mathrm {out}}}}}\leq 1$

Je nach Größe des Exponenten γ (gamma) unterscheidet man drei Fälle:

γ=1: I_out = I_in, die Abbildung ist linear.
γ < 1: Die Abbildung ist konkav. Kleine Eingabewerte werden stark gespreizt, große gestaucht.
γ > 1: Die Abbildung ist konvex. Kleine Eingabewerte werden gestaucht, große gespreizt.

In der Grafik sind drei Beispielkurven eingezeichnet für γ=3, 0,3 und 1.

Manchmal wird auch der Kehrwert des Exponenten als Gamma bezeichnet: γ → 1/γ

Geschichte

Der Normtext von DIN EN 61966-2 Anhang A (Farbmessung und Farbmanagement) verweist dabei auf die anfängliche Verwendung des Begriffs Gammakorrektur in der Fotografie durch Ferdinand Hurter und Vero Charles Driffield seit den 1890er Jahren. In der Fotografie wird er bisweilen synonym für Anstieg, Gradient und Kontrast benutzt. Definitionen für Bildschirmwiedergabe stammen von Irving Langmuir in den 1910er Jahren und von Oliver in den 1940er Jahren.

Zu unterscheiden sind auch „Elektronenkanonen“-Gammawerte von „Leuchtstoff“-Gammawerten. Die DIN EN-Norm 61966-A spricht deshalb von einer „Mehrdeutigkeit in der Definition des Begriffes 'Gamma'“ und empfiehlt, den Begriff in normativen Zusammenhängen nicht mehr zu verwenden.

Wahrnehmung und Gammakorrektur

Die vom Menschen empfundene Helligkeit steigt in dunklen Bereichen steiler und in hellen weniger steil an. Die Stevenssche Potenzfunktion ordnet dem menschlichen Auge dabei ein Gamma von ca. 0,3 bis 0,5 zu. Soll das Helligkeitssignal eines Anzeigegerätes, beispielsweise eines Monitors, linear wahrgenommen werden, muss es daher mit dem reziproken des obigen Gammawerts (ca. 3,3 bis 2) vorverzerrt werden, damit sich beide Nichtlinearitäten für den Betrachter am Ende wieder aufheben. Ein typischer Wert für Bildschirme ist etwa ein Gamma von 2,2.

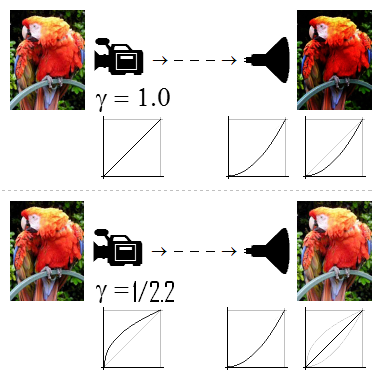oben: linearer Bildsensor (z.B. CCD) führt an Anzeige mit Gamma > 1 zu einem kontrastreichen aber unnatürlichen Bild
unten: Bildaufnehmer mit vorsätzlichem Gamma < 1 führt durch Anzeige mit passendem Gamma > 1 zu einem originalgetreu wahrnehmbaren Bild
(rechts unterhalb findet sich jeweils die Gamma-Kurve, die das Gesamtverhalten des Systems beschreibt)

Beispiel Monitore

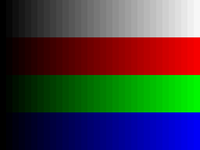
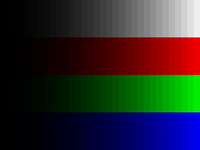
Das mittlere Originalbild zeigt einen Graustufenkeil und drei Stufenkeile in den gesättigten Farben Rot, Grün und Blau, die jeweils 32 Felder mit linear zunehmender Helligkeit haben. Das linke Bild zeigt das Bild nach einer Gammakorrektur mit dem Exponenten $\gamma =0{,}5$ und das rechte Bild nach einer Gammakorrektur mit dem Exponenten $\gamma =2{,}0$ . Die Helligkeiten der dunkelsten und hellsten Felder bleiben immer erhalten. Das jeweils 17. Feld von links hat im Originalbild ( $\gamma =1{,}0$ ) eine Helligkeit von 50 %, im linken Bild ( $\gamma =0{,}5$ ) eine Helligkeit von $0{,}5^{0{,}5}\approx 0{,}71=71\,\%$ und im rechten Bild eine Helligkeit von $0{,}5^{2{,}0}=0{,}25=25\,\%$ .

$\gamma =0{,}5$	$\gamma =1{,}0$	$\gamma =2{,}0$

Windows

Der Gamma-Wert eines durchschnittlichen mit Windows betriebenen Monitors liegt bei 2,2. Diese Einstellung empfiehlt sich, da fotografische Labore ebenfalls mit einem Gamma von 2,2 arbeiten, und so ein am Monitor für gut befundenes Bild auch dementsprechend belichtet wird. Über die Angabe eines Ausgabefarbprofils kann man das Gamma indirekt festsetzen. Hier bietet sich die Verwendung des sRGB-Profils für den „normalen“ Benutzer an, dem ein Gamma von näherungsweise 2,2 zu Grunde liegt.

macOS

Derselbe Monitor an einem Mac wurde bis vor kurzem standardmäßig mit einem Gamma von 1,8 betrieben. Die Gründe entstammen noch der Zeit vor dem Color Management des ICC. Ein Gamma von 1,8 war für einen Workflow ohne Farbmanagement gedacht, damit die Monitordarstellung besser der Tonwertreproduktion von Schwarzweißdruckern entsprach. Heutzutage werden die Gammawerte durch Farbprofile (z. B. vom ICC) ergänzt; das Standard-Mac-Farbprofil enthält dabei ein Gamma von 1,8. Ab Mac OS X 10.6 (Snow Leopard) liegt der Standard-Gammawert bei 2,2.

Gamma-Testgrafik

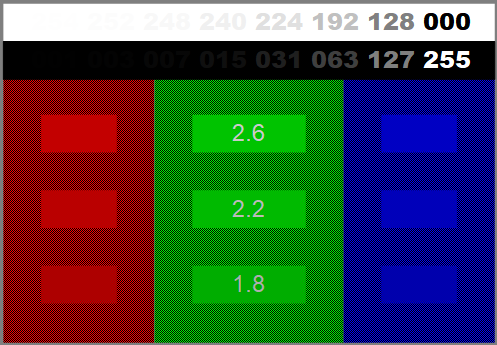
Kontrast-, Helligkeit- und Gamma-Testbild. Nur gültig bei einem Web-Browser-Zoom von 100 %

Im Gamma-Testbild besteht ein einzelner farbiger Bereich zum Großteil aus einem karierten Muster mit 0 % und 100 % Helligkeit. Das Auge des Beobachters sieht dies als 50 % relative Leuchtdichte und integriert sie zu einer Helligkeit gemäß $Helligkeit=Leuchtdichte^{(1/\gamma )}$ . Dieser Zusammenhang ist als Weber-Fechner-Gesetz, genauer Stevenssche Potenzfunktion, bekannt und gilt für alle Sinnesorgane. Die einfarbigen Bereiche haben eine Helligkeit entsprechend dem eingetragenen Gamma-Wert. Ein Gamma von 1,0 hat die Helligkeit 50 %, Gamma 1,8 hat 68 % und Gamma 2,2 hat 73 %.

Die beiden oberen Balken erlauben die Kalibrierung von Kontrast und Helligkeit. In jedem Balken werden acht dreistellige Zahlen dargestellt. Ein gut eingestellter Monitor zeigt in beiden Balken die rechten sechs Zahlen, ein schlechter Monitor zeigt nur die rechten vier Zahlen.

Die Farben werden wegen der Farbempfindlichkeit des Auges in der Reihenfolge Grün, Rot und Blau abgeglichen. Der Abgleich erfolgt entweder über die Farbausgleich-Anpassung (color balance) des Betriebssystems oder über die primärfarbenindividuelle Helligkeitseinstellung des Grafikkarten-Konfigurationsprogramms. Ab MS-Windows 7 gibt es das Programm dccw.exe, mit dem Gammakorrektur und Farbanpassung auf Betriebssystem-Ebene eingestellt wird. Andere Programme können auch ein ICC-Profil erstellen und laden. Siehe Monitorkalibrierung für eine Anleitung zur Einstellung für eine gute Wiedergabe von Monitor, Grafikkarte und Betriebssystem.

Hat man so den tatsächlichen Gamma-Wert seines Monitors herausgefunden, kann man mit Hilfe der Grafikeinstellungen seines Computers einen eigenen, von den Werksvorgaben unabhängigen Wert einstellen. Indem man in den Grafikeinstellungen den Kehrwert des gefundenen Wertes als Gamma einstellt, wird die Gamma-Korrektur des Monitors (theoretisch) neutralisiert; es ergibt sich ein tatsächlicher Gamma-Wert von 1. Will man einen tatsächlichen Gamma-Wert von z. B. 2,2 erhalten, so muss man den Kehrwert mit 2,2 multiplizieren und diesen Wert als Gamma-Wert einstellen. Hat man z. B. einen tatsächlichen Gamma-Wert von 1,3 festgestellt, so muss man in den Grafikeinstellungen den Wert 0,77 einstellen, um die Gamma-Korrektur zu neutralisieren, und 1,69, um den tatsächlichen Gamma-Wert von 2,2 zu erreichen.

Beispiel Bildbearbeitung

Tonwertkorrekturen wie Änderungen der Helligkeit, des Kontrasts usw. überführen Farbwerte eines Bildes in andere Farbwerte desselben Farbraums. Ist die Korrekturfunktion dabei eine Potenzfunktion der Form A=E, spricht man von einer Gammakorrektur. In grober Vereinfachung hebt eine solche Korrektur bei Verwendung von Gammawerten < 1 zu dunkle Bildpartien in ihrer Helligkeit an, während sie bei Verwendung von Gammawerten > 1 – umgekehrt – zu helle Bildpartien wieder in ihrer Helligkeit zurücknimmt. Bei einem Gammawert = 1 schließlich bleibt, da E¹ = E ist, alles beim alten.

Manche Bildbearbeitungsprogramme (z.B. GIMP) geben bei der Gammakorrektur nicht den Gammawert selbst, sondern den Kehrwert 1/Gamma an, so dass eine Erhöhung des Wertes einer Erhöhung der Helligkeit entspricht.

Helligkeits-, Kontrast- und Gammakorrektur im Vergleich

Ursprungsbild
Bild selektiv aufgehellt mit $\gamma$ = 0,3
Bild selektiv abgedunkelt mit $\gamma$ = 3

Wird bei einem zu dunklen Bild der Helligkeitswert erhöht, so werden alle Farbtöne um den gleichen Wert aufgehellt. Die hellsten und die dunkelsten Farbtöne gehen verloren. Die sehr hellen Töne werden zu reinem Weiß. Schwarz und die sehr dunklen Töne werden zu einem Grauton. Insgesamt reduziert sich also das Helligkeitsspektrum des Bildes und es scheint sich ein heller Schleier über das Bild zu legen. Durch eine Erhöhung des Kontrasts kann dies teilweise ausgeglichen werden. Die dunklen Farbtöne werden so wieder hergestellt. Die Umwandlung der hellen Töne zu Weiß vergrößert sich jedoch noch.

Die Aufhellung eines Bildes durch die Änderung des Gamma-Werts hat demgegenüber den Vorteil, dass die dunklen Töne stärker aufgehellt werden als die Hellen. Auch bleibt das Helligkeitsspektrum insgesamt erhalten. Das Spektrum (die Varianz) der hellen Töne wird "gestaucht", während das der dunklen Töne sich vergrößert.

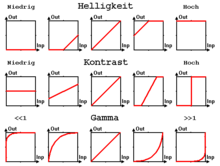
Viele Bildbearbeitungsprogramme bieten die Möglichkeit, die in der Grafik abgebildeten Korrekturkurven individuell zu bearbeiten, um sie der gewünschten Helligkeitsverteilung bzw. der des Ursprungsbildes anzupassen.

Wird die Korrekturfunktion mit einem Koeffizienten multipliziert ( $A=k\cdot E^{\gamma }$ ), ergibt sich daraus zusätzlich zu der eigentlichen Gammakorrektur noch eine Kontrasterhöhung ( k>1 ) bzw. -verminderung ( k<1 ), bei Hinzufügen einer additiven Konstante dagegen ( $A=E^{\gamma }+h$ ) über die Gammakorrektur hinaus eine Helligkeitserhöhung ( h>0 ) bzw. -verminderung ( h<0 ). In der Praxis führen so allein schon die beiden eben genannten zusätzlichen Optionen schnell zu einer verwirrenden Vielfalt von Korrekturmöglichkeiten – die obige Abb. rechts zeigt daher noch einmal separat das jeweils Charakteristische der Helligkeits-, Kontrast- und Gammawertkorrektur.

Beispiel digitale Videotechnik

Betrachtet wird zunächst ein abbildendes System mit ideal-linearem Verhalten:

1. Beispiel: Ein CCD-Chip (z.B. DV-Cam) nimmt einen – für das menschliche Sehen ausgelegten – Graukeil auf. Der Chip liefert zu den einzelnen Farbfeldern nichtlinear ansteigende Spannungen, da die Felder nichtlinear ansteigende Reflexionsgrade aufweisen, denn diese Felder wurden von einem Menschen optisch durch seine Hellempfindung geeicht (siehe auch Weber-Fechner-Gesetz). Die gespeicherten Werte werden nun auf einem ideal-linear arbeitenden Fernseher wieder ausgegeben. Das Ergebnis würde zufriedenstellend sein, da wiederum nichtlineare Werte zu der gleichen Hellempfindung wie der abgefilmte Graukeil führen würden.

Soweit das einfachste Beispiel eines geschlossenen Systems, das genau aufeinander abgestimmt ist und alle informationstechnischen Anforderungen missachtet. In der Realität haben wir es aber mit offenen Systemen zu tun und wollen die Daten über die Kamera am Computer bearbeiten, diese auf den unterschiedlichen Ausgabemedien ausgeben und immer dasselbe Ergebnis sehen.

2. Beispiel: Die DV-Cam nimmt wieder denselben Graukeil auf. Die Ausgangsspannungen des CCD-Chips werden normiert, so dass der Wertebereich in einem Intervall von [0,1] liegt. Die Werte durchlaufen nun beispielsweise die folgende Funktion:; Für ein $\gamma _{{\text{1}}}$ von 0,45 gilt:; $A=E^{{0{,}45}}$; Nun kann man vereinfacht sagen, dass die Werte an das optische System des Menschen angepasst sind. (In der Realität werden die einzelnen Farbkanäle an die Farbreizfunktion des Auges angepasst, siehe Normspektralwertkurve). Normiert man die Werte so, dass diese im Wertebereich von [0,255] liegen, erhalten wir die bekannten 8-Bit-RGB-Tripel, die linear zu unserer Hellempfindung ansteigen. Dies ermöglicht nun verschiedene Operationen der digitalen Bildverarbeitung.; Schreiten wir zur Ausgabe der Bilddaten fort:; Um die Daten für das menschliche Auge richtig abzubilden, müssen diese wiederum angepasst werden, da ein linearer Anstieg der Spannung bei einem ideal-linear arbeitenden Bildschirm keine lineare Hellempfindung hervorrufen würde. Also passen wir die Werte durch eine erneute Gammakorrektur an das Auge an. Zuvor werden die Werte natürlich wieder auf 1 normiert.; Nun mit einem $\gamma _{{\text{2}}}$ von üblicherweise 2,2 (PC) → dies ergibt sich aus dem Kehrwert von 0,45:; ${\frac {1}{0{,}45}}\sim 2{,}2\quad \Rightarrow \quad A=E^{{2{,}2}}$

Das Resultat entspricht der abgefilmten Graukarte.

Da es keine ideal-linearen Systeme gibt, müssen bei diesem Prozess noch zwei (bzw. sechs) Gammakorrekturen hinzugefügt werden. Zum einen hat der Chip ein nichtlineares Verhalten für die drei Farbkanäle unterschiedlicher Art. Diese müssen durch jeweils eine weitere Gammakorrektur ausgeglichen werden. Zum anderen verhalten sich die drei Leuchtstoffe eines Bildschirms nichtlinear. Die Farbkorrekturen sind bauteilbedingt und werden in der Regel schon in den Geräten selbst implementiert. Nur das Alter eines Geräts lässt das Resultat dieser Korrektur verschlechtern. Der Anwender bekommt von diesen Korrekturen in der Regel nichts mit. Ist die Korrektur veraltet, entsteht meist ein Farbkippen (ein Farbstich unterschiedlicher Färbung und Intensität über einem Graukeilverlauf).

Jedes abbildende System muss sich mit dem Problem der Helligkeitsempfindung auseinandersetzen. Dadurch ist eine Fülle von Gammakorrekturen entstanden. Die Farbfernsehsysteme PAL und NTSC, die Betriebssysteme Microsoft Windows und Mac OS Classic sowie unixoide Systeme, aber auch Druckerhersteller kennen das Problem.

Gammakorrektur zur Linearisierung

RGB-Monitore und TV-Geräte haben verschiedene Helligkeitsprofile und erfordern häufig eine Korrektur, um das Bild optimal darzustellen.

Idealerweise würde ein Ausgabegerät den Helligkeitswert 0 als Schwarz und den Helligkeitswert 1 als Weiß abbilden und alle dazwischen liegenden Werte linear zwischen Schwarz und Weiß als unterschiedliche Grauwerte darstellen. Dies entspräche einem Gamma von 1.

Aufgrund produktionstechnisch bedingter Faktoren ist eine solche Linearität bei Aufnahmegeräten (z.B. Kameras) oder Ausgabegeräten (z.B. Bildröhren) nicht zu erreichen. Meist spielt die nichtlineare Eingangskennlinie eines Bildwandlers (z.B. eines LCDs) oder eines Kamera-CCD-Chips die entscheidende Rolle. Das heißt, dass bei einem Bild mit konstanter Helligkeitsänderung von Schwarz nach Weiß bei einem Gamma abweichend von 1 entweder die hellen und dunklen Stellen überproportional detailliert abgebildet werden oder aber die mittleren Graustufen.

Damit im weiteren Produktionsweg keine Helligkeitsinformationen verloren gehen oder aber überbetont dargestellt werden, hat jedes Gerät, das eine nichtlineare Übertragungsfunktion besitzt, die Möglichkeit einer Gammakorrektur zur Linearisierung der Abbildungsleistung.

Besitzt ein Gerät mehrere Bildwandler für unterschiedliche Farben, wie z.B. eine Dreiröhrenkamera, so kann dort aufgrund unterschiedlicher Empfindlichkeiten eine Gammakorrektur für jeden einzelnen Farbkanal notwendig sein.

Die Gammakorrektur ist in der digitalen Bildverarbeitung auch als Potenztransformation bekannt.

Details

Der Zusammenhang zwischen den digitalen und den radiometrischen Daten wird in der Literatur als die Kathodenstrahlröhren-Übertragungsfunktion $\gamma$ (Gamma) bezeichnet. Der besseren Übersichtlichkeit halber werden wir diese Gesamtfunktion in zwei Teile, den digitalen Teil D (Grafikkarte) und den analogen Teil A (Monitoreingang, Bildschirm), aufspalten.

Der Zusammenhang zwischen der Monitoreingangsspannung und der resultierenden Helligkeit (Leuchtdichte) des einzelnen Bildpunktes, also unsere Funktion A, folgt einer allgemeinen Potenzfunktion. Im einfachsten Modell ist:

$A\sim E^{\gamma }$

mit : auf 1 normierte Eingangsspannung und : auf 1 normiert Helligkeit.

Grundlage dafür ist das Verhalten der beschleunigten Elektronen innerhalb der Bildröhre, wobei der Haupteffekt auf der abschirmenden Wirkung der Elektronenwolke in der Umgebung der Kathode beruht. Dieses einfache Modell wird durch die Hinzunahme von Konstanten erweitert, die diverse Monitorparameter abbilden. Das Optimum wäre ein linearer Zusammenhang mit Nullpunkt bei Null, maximales Ausgangssignal bei maximalem Eingangssignal sowie linearem Zusammenhang, d.h. $\gamma =1$ .

Die Leuchtdichteabhängigkeit der Farbphosphore bezüglich der Stromstärke ist ebenfalls mit einer Potenzfunktion beschreibbar, deren Exponent bei ca. 0,9 liegt. Daraus ergibt sich ein Gesamtexponent $\gamma$ zu 1,6 (Fernsehen) über 1,8 (Mac-Systeme) bis 2,2 (IBM-PC-kompatible Systeme) für Computermonitore.

Die resultierende Abhängigkeit kann beschrieben werden durch:

$A=H(aE+h)^{\gamma }$

mit den Parametern

: Intensität [0..H]

: maximale Helligkeit der Bildröhre

: Verstärkung (Kontrast)

: Offset (Helligkeit)

: normalisierter Pixelfarbwert, einfach zusammenhängende Teilmenge aus [0..1], typische Pixelfarbwerte liegen im Intervall [0..255]

$\gamma$ : Gammaexponent

Ursprung

D: optische Dichte / H: Belichtung

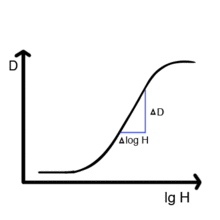
Der Begriff des Gammas wurde erstmals in der Sensitometrie, also zur Beschreibung der Empfindlichkeit von fotografischem Material, eingeführt, wobei es neben dem Gamma-Wert auch verschiedene andere, fotografisches Material in dieser Hinsicht charakterisierende Parameter gibt.

Zur Bestimmung des Gamma-Werts eines fotografischen Materials, z.B. Schwarzweiß-Films oder -Fotopapiers, untersucht man mit Hilfe einer Dichte- oder Gradationskurve (siehe Beispielbild) die Steilheit seiner optischen Dichte, d.h. Schwärzung, in Abhängigkeit von der Belichtung und definiert dabei als Gamma-Wert ( $\gamma$ ) die Steigung einer Tangente an den geradlinigen Teil dieser Kurve. Da die Schwärzung von Fotomaterial logarithmisch mit der Belichtung zunimmt, muss dabei in der mathematischen Formulierung dieses Zusammenhangs statt der Belichtung selbst ihr Logarithmus verwendet werden:

$\gamma ={\frac {\Delta D}{\Delta \log H}}$ .

Anhand des so ermittelten Gamma-Werts kann man anschließend z.B. Fotopapiere nach ihrer Gradation in „harte“ und „weiche“ unterscheiden, d.h. solche, die auf eine Zunahme der Belichtung empfindlicher als „normal“ reagieren, oder auch weniger empfindlich. Fälschlicherweise wird der dabei beobachtete Gamma-Wert oft auch zur Beschreibung linearer Tonwertkorrekturen (s.o.) herangezogen, obwohl er in diesem Zusammenhang eher ein Maß für den Kontrast des Bildes ist.

Simulation von „weichem“ Fotopapier mit linearem $\gamma =0{,}25$
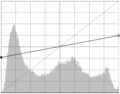Histogramm für eine „weiche“ lineare Tonwertkorrektur
Simulation von „hartem“ Fotopapier mit linearem $\gamma =4$
Histogramm für eine „harte“ lineare Tonwertkorrektur

Basierend auf einem Artikel in:

Wikipedia.de