
Exzentrizität (Mathematik)

Der Ausdruck Exzentrizität hat in der Mathematik zwei verwandte Bedeutungen im Zusammenhang mit nicht ausgearteten Kegelschnitten (Ellipsen, Hyperbeln, Parabeln):

- Die lineare Exzentrizität ist bei einer Ellipse
bzw. Hyperbel
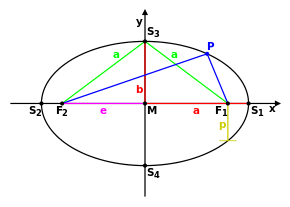
der Abstand eines Brennpunkts zum Mittelpunkt und wird mit
bezeichnet (s. Bild). Sie hat die Dimension einer Länge. Da ein Kreis eine Ellipse mit zusammenfallenden Brennpunkten ist
, gilt für den Kreis
.
- Die numerische Exzentrizität
ist für Ellipsen und Hyperbeln das Verhältnis
der linearen Exzentrizität zur großen Halbachse und damit eine dimensionslose Zahl.
-
- Für eine Ellipse gilt
. Im Fall
ist die Ellipse ein Kreis.
- Die numerische Exzentrizität beschreibt hier die mit wachsendem
zunehmende Abweichung einer Ellipse von der Kreisform.
- Für eine Hyperbel gilt
. Mit wachsendem
wird die Hyperbel immer offener, d.h., der Winkel zwischen den Asymptoten wächst. Gleichseitige Hyperbeln, also solche mit rechtwinkligen Asymptoten, ergeben sich für
.
- Für eine Parabel definiert man
(zur Motivation s. unten).
- Für eine Ellipse gilt
- Die Bedeutung der numerischen Exzentrizität ergibt sich aus dem Umstand,
dass Ellipsen bzw. Hyperbeln genau dann ähnlich
sind, wenn sie dieselbe numerische Exzentrizität aufweisen. Parabeln (
) sind immer ähnlich.
Bei Ellipsen und Hyperbeln wird der Abstand
der Brennpunkte vom Mittelpunkt auch Brennweite genannt. Bei einer
Parabel hingegen wird der Abstand des Brennpunkts vom Scheitel als
Brennweite bezeichnet.
In der Astronomie
wird meist nur die numerische Exzentrizität verwendet und einfach
Exzentrizität genannt, dabei aber abweichend von der Notation in der
Mathematik oft mit
bezeichnet.
Mathematische Behandlung

Mit Exzentrizität beschrieb man zunächst die Abweichung einer Ellipse
von der Kreisform.
Als Maß für diese Abweichung verwendete man den Abstand
eines Brennpunkts zum Mittelpunkt (siehe 1. Bild). Für
erhält man einen Kreis. Da eine Hyperbel auch einen Mittelpunkt und Brennpunkte
besitzt, wurde die Bezeichnung auf den Hyperbelfall ausgedehnt, obwohl man hier
nicht von der Nähe einer Hyperbel zu einem Kreis sprechen kann. Eine Parabel
besitzt keinen Mittelpunkt und damit zunächst auch keine Exzentrizität.
Eine weitere Möglichkeit, die Abweichung einer Ellipse von der Kreisform zu
beschreiben, ist das Verhältnis .
Es ist
.
Auch hier erhält man für
einen Kreis. Im Fall
ist der Parameter
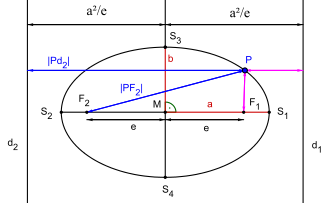
auch das zur Leitliniendefinition einer Ellipse verwandte Verhältnis zwischen
dem Abstand eines Ellipsenpunkts zum Brennpunkt und dem Abstand zu einer
Leitlinie (siehe 4. Bild). (Ein Kreis lässt sich nicht mithilfe einer
Leitlinie definieren.) Lässt man bei der Leitliniendefinition für
auch Werte gleich oder größer 1 zu, erhält man als Kurve eine Parabel, falls das
Verhältnis
ist, und Hyperbeln
im Fall
.
Der Parameter
erlaubt es also, Ellipsen, Parabeln und Hyperbeln mit einem gemeinsamen
Scharparameter zu beschreiben. Zum Beispiel beschreibt die Gleichung
(s. 3. Bild)
alle Ellipsen (incl. Kreis), die Parabel und alle Hyperbeln, die den
Nullpunkt als gemeinsamen Scheitel, die x-Achse als gemeinsame Achse und
denselben Halbparameter
(siehe 1. Bild) haben. (
ist auch der gemeinsame Krümmungskreisradius
im gemeinsamen Scheitel, s. Ellipse, Parabel, Hyperbel).
- Der Parameter
existiert nur im Falle von Ellipsen und Hyperbeln und heißt lineare Exzentrizität.
ist eine Länge.
- Für die Ellipse
ist
.
- Für
ist
und die Ellipse ein Kreis. Ist
nur wenig kleiner als
, d.h.
ist klein, dann ist die Ellipse sehr flach.
- Für die Hyperbel
ist
und damit für jede Hyperbel
.
- Der Parameter
existiert für Ellipsen, Hyperbeln und Parabeln und heißt numerische Exzentrizität.
ist das Verhältnis zweier Längen, ist also dimensionslos.
- Für Ellipsen und Hyperbeln gilt
, für Parabeln
.
Fasst man eine Ellipse/Parabel/Hyperbel als ebenen Schnitt eines senkrechten Kreiskegels auf, lässt sich die numerische Exzentrizität durch
ausdrücken. Dabei ist
der Neigungswinkel einer Kegelerzeugenden und
der Neigungswinkel der schneidenden Ebene (s. Bild).
Für
ergeben sich Kreise und für
Parabeln. (Die Ebene darf die Kegelspitze nicht enthalten.)
Literatur
- Kleine Enzyklopädie Mathematik. Verlag Harri Deutsch, 1977, ISBN 3-87144-323-9, S. 192, 195, 328, 330.
- Hans-Jochen Bartsch: Taschenbuch mathematischer Formeln für Ingenieure und Naturwissenschaftler. Hanser, 2014, ISBN 978-3-446-43735-7, S. 287–289.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.09. 2022