Parameterform
Die Parameterform oder Punktrichtungsform ist in der Mathematik eine spezielle Form einer Geradengleichung oder Ebenengleichung. In der Parameterform wird eine Gerade durch einen Ortsvektor (Stützvektor) und einen Richtungsvektor dargestellt. Jeder Punkt der Geraden wird dann in Abhängigkeit von einem Parameter beschrieben. Eine Ebene wird durch einen Stützvektor und zwei Richtungsvektoren dargestellt. Jeder Punkt der Ebene wird dann in Abhängigkeit von zwei Parametern beschrieben. Bei der Parameterform handelt es sich also um eine spezielle Parameterdarstellung.
Parameterform einer Geradengleichung
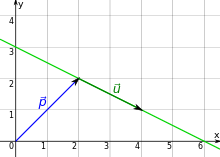
Darstellung
In der Parameterform wird eine Gerade in der Ebene durch einen Stützvektor
und einen Richtungsvektor
beschrieben. Eine Gerade besteht dann aus denjenigen Punkten in der Ebene, deren
Ortsvektoren
die Gleichung
mit
erfüllen. Der Stützvektor ist dabei der Ortsvektor
eines beliebigen Punkts auf der Geraden, der auch als Aufpunkt bezeichnet wird.
Der Richtungsvektor ist der Differenzvektor (Verbindungsvektor) zu einem
beliebigen weiteren Punkt der Geraden. In der Parameterform werden die Punkte
der Geraden in Abhängigkeit von dem Parameter
dargestellt. Jedem Wert von
entspricht genau ein Punkt der Geraden. Durchläuft der Parameter die reellen
Zahlen, so erhält man alle Punkte der Geraden. Ist
ein Einheitsvektor,
dann gibt
gerade den Abstand eines Punkts auf der
Geraden vom Aufpunkt an.
Beispiel
Ausgeschrieben lautet die Parameterform einer Geradengleichung
mit .
Im Bild oben ist der Stützvektor
und der Richtungsvektor
,
man erhält als Geradengleichung
.
Jede Wahl von ,
beispielsweise
oder
,
ergibt dann einen Geradenpunkt.
Berechnung
Aus der Zweipunkteform
Aus der Zweipunkteform
einer Geradengleichung lässt sich ein Richtungsvektor der Geraden als
Differenzvektor zwischen den Ortsvektoren
und
der beiden Punkte erhalten, das heißt
.
Als Stützvektor
kann der Ortsvektor eines der Punkte verwendet werden.
Aus der Normalenform
Aus der Normalenform
einer Geradengleichung kann ein Richtungsvektor der Geraden bestimmt werden,
indem die beiden Komponenten des Normalenvektors
der Geraden vertauscht werden und bei einer der beiden Komponenten das
Vorzeichen geändert wird, das heißt
.
Der Stützvektor
kann aus der Normalenform übernommen werden.
Aus der Koordinatenform
Aus der Koordinatenform
einer Geradengleichung mit den Parametern
und
lässt sich ein Normalenvektor der Gerade direkt als
ablesen und damit ein Richtungsvektor der Gerade analog zur Normalenform über
ermitteln. Einen Stützvektor der Gerade erhält man, je nachdem ob
oder
ungleich null ist, durch Wahl von
oder
.
Analog lassen sich auf diese Weise auch aus der Achsenabschnittsform und der hesseschen Normalform ein Stützvektor und ein Richtungsvektor berechnen.
Verallgemeinerung
Allgemein lassen sich durch die Parameterform nicht nur Geraden in der Ebene,
sondern auch Geraden im drei- oder höherdimensionalen Raum beschreiben. Im -dimensionalen
euklidischen
Raum besteht eine Gerade entsprechend aus denjenigen Punkten, deren
Ortsvektoren
die Gleichung
mit
erfüllen. Es wird dabei lediglich mit -komponentigen
statt zweikomponentigen Vektoren gerechnet.
Parameterform einer Ebenengleichung
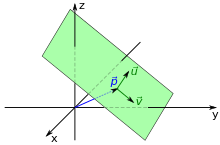
Darstellung
In der Parameterform wird eine Ebene im dreidimensionalen Raum durch einen
Stützvektor
und zwei Richtungsvektoren
und
beschrieben. Eine Ebene besteht dann aus denjenigen Punkten im Raum, deren
Ortsvektoren
die Gleichung
mit
erfüllen. Der Stützvektor ist dabei der Ortsvektor eines beliebigen Punkts in
der Ebene, der wiederum als Aufpunkt bezeichnet wird. Die beiden
Richtungsvektoren, hier auch Spannvektoren genannt, müssen in der Ebene liegen
und ungleich dem Nullvektor
sein. Sie dürfen auch nicht kollinear
sein, das heißt
darf sich nicht als Vielfaches
von
schreiben lassen und umgekehrt. In der Parameterform werden die Punkte der Ebene
in Abhängigkeit von den zwei Parametern
und
dargestellt. Jedem Wertepaar dieser Parameter entspricht dann genau ein Punkt
der Ebene. Die Richtungsvektoren spannen somit ein affines Koordinatensystem
auf, wobei
die affinen
Koordinaten eines Punkts der Ebene sind.
Beispiel
Ausgeschrieben lautet die Parameterform einer Ebenengleichung
mit .
Ist beispielsweise der Stützvektor
und sind die Richtungsvektoren
und
,
so erhält man als Ebenengleichung
.
Jede Wahl von ,
beispielsweise
oder
,
ergibt dann einen Ebenenpunkt.
Berechnung
Aus der Dreipunkteform
Aus der Dreipunkteform
einer Ebenengleichung lassen sich zwei Richtungsvektoren der Ebene als
Differenzvektoren zwischen den Ortsvektoren ,
und
jeweils zweier Punkte erhalten, also
und
.
Als Stützvektor
kann der Ortsvektor eines der Punkte verwendet werden.
Aus der Normalenform
Aus der Normalenform
einer Ebenengleichung können aus dem Normalenvektor
zwei Richtungsvektoren der Ebene durch Setzen von
und
bestimmt werden. Sollte einer dieser beiden Vektoren gleich dem Nullvektor sein, kann
stattdessen der Vektor
gewählt werden. Der Stützvektor
kann aus der Normalenform übernommen werden.
Aus der Koordinatenform
Aus der Koordinatenform
einer Ebenengleichung mit den Parametern
und
lässt sich ein Normalenvektor der Ebene als
ablesen und damit zwei Richtungsvektoren der Ebene über
und
ermitteln. Sollte einer dieser beiden Vektoren gleich dem Nullvektor sein,
kann stattdessen der Vektor
gewählt werden. Einen Stützvektor erhält man, je nachdem welche der Zahlen
ungleich null ist, durch Wahl von
oder
.
Analog lassen sich auf diese Weise auch aus der Achsenabschnittsform und der hesseschen Normalform ein Stützvektor und ein beziehungsweise zwei Richtungsvektoren berechnen.
Verallgemeinerung
Allgemein lassen sich durch die Parameterform nicht nur Ebenen im
dreidimensionalen Raum, sondern auch in höherdimensionalen Räumen beschreiben.
Im -dimensionalen
euklidischen Raum besteht eine Ebene entsprechend aus denjenigen Punkten, deren
Ortsvektoren
die Gleichung
mit
erfüllen. Es wird dabei lediglich mit -komponentigen
statt dreikomponentigen Vektoren gerechnet.
Siehe auch
Literatur
- Steffen Goebbels, Stefan Ritter: Mathematik verstehen und anwenden. Springer, 2011, ISBN 978-3-8274-2762-5.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 02.05. 2021