
Ortho- und Parawasserstoff
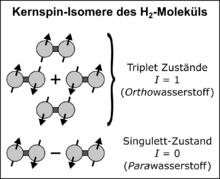
Ortho- und Parawasserstoff (kurz oH2 und pH2) sind zwei Formen des di-Wasserstoffmoleküls, die sich in der Symmetrie ihrer Kernspinkonfiguration und Rotationszustände unterscheiden. Obwohl sie die gleiche chemische Struktur haben, weisen sie teilweise verschiedene physikalische Eigenschaften auf. Wasserstoff ist im Allgemeinen ein Gemisch aus beiden Spezies; das Gleichgewichtsmischverhältnis ist dabei eine Funktion der Temperatur. Die Existenz der beiden Formen muss z.B. bei der Verflüssigung von Wasserstoff berücksichtigt werden, insbesondere, wenn dieser als Raketentreibstoff genutzt werden soll. Zudem kann die Symmetrie-Ordnung von Parawasserstoff für die Signalverstärkung der Kernspinresonanz (Hyperpolarisierung), für Kernspinresonanzspektroskopie (NMR) und Magnetresonanztomographie (MRT) ausgenutzt werden.
Physikalische Grundlagen
Da Wasserstoffkerne Spin-1/2-Teilchen sind, folgen sie der Fermi-Dirac-Statistik. Daher muss der quantenmechanische Zustand des ganzen Wasserstoffmoleküls (H2) antisymmetrisch bezüglich einer Vertauschung der beiden Protonen sein (Pauli-Prinzip). Dazu muss die Gesamt-Wellenfunktion der beiden Kerne antisymmetrisch sein. Diese ist als Produkt aus Orts- (Bahndrehimpuls) und Spin-Wellenfunktion der beiden Protonen des H2-Moleküls darstellbar und genau dann antisymmetrisch, wenn einer der beiden Faktoren des Produkts antisymmetrisch ist und der andere symmetrisch.
Nach Drehimpulsaddition des Kernspins finden sich vier Eigenzustände der
Kernspin-Wellenfunktion: drei Triplett-Zustände mit
Gesamtspin
I = 1 und magnetischen Spinquantenzahlen M = −1, 0, 1 sowie ein
Singulett-Zustand
mit I = 0 und M = 0. Die drei Triplett-Zustände sind symmetrisch
und werden Ortho-Zustände genannt (Orthowasserstoff, kurz
oH2); der Singulett-Zustand ist antisymmetrisch und wird auch
Para-Zustand genannt (Parawasserstoff, kurz
pH2). In der Dirac-Notation
schreiben sich die vier Eigenzustände so:
Da die Gesamtwellenfunktion antisymmetrisch bei Vertauschung der beiden
Protonen ist, muss die Ortswellenfunktion zum Bahndrehimpuls
beim Triplett- oder Ortho-Zustand (symmetrisch bezüglich des Kernspins der
Protonen) antisymmetrisch sein (
ungerade) und beim Singulett- oder Para-Zustand (antisymmetrisch bezüglich des
Kernspins) symmetrisch (
gerade).
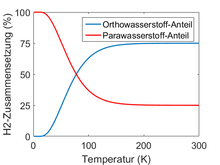
Im Allgemeinen ist Wasserstoff ein Gemisch aus oH2 und pH2 (bzw. aller vier Kernspin-Eigenzustände); die temperaturabhängige Gleichgewichtsverteilung genügt dabei der Boltzmann-Statistik. Da die Energieaufspaltung zwischen den Kernspinzuständen im Vergleich zu den Rotationsenergien vernachlässigbar klein ist, entscheiden Letztere effektiv über den energetischen Grundzustand des H2-Moleküls. Daher ist pH2 die energetisch günstigere und oH2 die energiereichere Form. Das temperaturabhängige Gleichgewichtsverhältnis von oH2/pH2 wird beschrieben durch
,
wobei
die Rotationstemperatur ist (
,
mit der Rotationskonstanten B). Der Grenzwert
für hohe Temperaturen ist also
und entspricht einer Gleichverteilung der vier Kernspin-Zustände (75 %
oH2 und 25 % pH2). Das entspricht
gerade dem Entartungsverhältnis
der Kernspin-Zustände (Ortho mit Gesamtspin 1 drei Zustände, Para
mit Gesamtspin 0 nicht entartet, das heißt, nur ein Zustand). Bei Raumtemperatur
ist dieses Verhältnis schon nahezu erreicht. Für niedrige Temperaturen (
)
gilt
,
der Grenzwert 0 entspricht 100 % pH2.
Die Übergänge zwischen oH2 und pH2 sind bei normalem Druck und nicht zu hoher Temperatur in der Gasphase aufgrund der Symmetrieerhaltung extrem selten (reine Kernspin-Übergänge sind sogar verboten) und die Umwandlung, also die Annäherung an die Gleichgewichtsverteilung, verläuft entsprechend langsam. Dieser Prozess kann jedoch mit homogener sowie heterogener Katalyse, etwa mit Aktivkohle, beschleunigt werden.
Physikalische Eigenschaften
Das Verhalten der spezifischen Wärme von Wasserstoff, insbesondere bei tiefen Temperaturen, blieb lange Zeit ungeklärt. 1912 hatte Arnold Eucken den Abfall des Rotationsanteils der spezifischen Wärme beim gasförmigen Wasserstoff zwischen 300 und 60 Kelvin beobachtet, was damals theoretisch nicht erklärt werden konnte. Ebenso hatte Reinhard Mecke um 1922 einen Intensitätswechsel im Verhältnis 1:3 in den Bandenspektren zweiatomiger Moleküle mit identischen Atomen entdeckt. Erst nach der Entwicklung der Quantenmechanik konnte Werner Heisenberg 1926 zeigen, dass die zwei Spin-Isomere des H2-Moleküls ursächlich dafür sind, wobei er in Analogie zu den Elektronen beim Ortho- und Para-Helium vorging. Heisenberg wurde später „für die Erschaffung der Quantenmechanik, deren Anwendung, unter anderem, zur Entdeckung der verschiedenen Formen des Wasserstoffs geführt hat“ mit dem Nobelpreis für Physik ausgezeichnet. Ortho- und Parawasserstoff unterscheiden sich in einigen grundlegenden physikalischen Eigenschaften. So weisen sie deutlich verschiedene Wärmekapazitäten, aber auch abweichende elektrische Leitfähigkeiten sowie verschiedene Temperaturabhängigkeiten dieser zwei Größen auf. Außerdem ist oH2 mit der Methode der Kernspinresonanz (NMR) messbar, während pH2 mit Gesamtspin I = 0 „NMR-unsichtbar“ ist. Abgesehen hiervon sind die physikalischen Eigenschaften nur geringfügig verschieden. Beispielsweise liegen der Schmelz- und Siedepunkt der para-Form etwa 0,1 K unter denen der ortho-Form.
Anwendungen
Herstellung und Lagerung von flüssigem Wasserstoff
Da die Zustände des Parawasserstoffs energetisch günstiger sind als die des Orthowasserstoffs, wird die Energiedifferenz bei der ortho-para-Umwandlung in Form von Wärme frei. Wie oben erwähnt, ist die Umwandlung jedoch langsam, wodurch sie beim Abkühlen und Verflüssigen (≈ 21 K) unter normalen Bedingungen zeitverzögert abläuft. Die frei werdende Energie (Umwandlungsenthalpie) ist mit 1544 J/mol größer als die Verdampfungswärme (904 J/mol), die notwendig ist, um flüssigen Wasserstoff in den gasförmigen Zustand zu überführen. Daher verdampft aufgrund der ortho-para-Umwandlung auch bei vollkommener Wärmeisolierung ein signifikanter Teil des flüssigen Wasserstoffs, wenn bei der Verflüssigung nicht entsprechende Vorkehrungen getroffen werden. Bei der industriellen Herstellung von flüssigem Wasserstoff wird die Umwandlung beim Abkühlen daher noch in der Gasphase katalytisch beschleunigt.
Raketenantrieb
Flüssiger Wasserstoff wird als Raketentreibstoff bei Wasserstoff-Sauerstoff-basierten Raketentechnologien verwendet, wodurch größere Mengen H2 mitgeführt werden können. Auch hier wäre eine beschleunigte Verdampfung durch die oH2-pH2 Umwandlung unerwünscht, weswegen flüssiger Wasserstoff im thermischen Gleichgewicht getankt wird.
Parawasserstoff bei NMR und MRT
Angereicherter Parawasserstoff wird in Chemie und Medizin genutzt, um das Kernspinresonanzsignal (Messgröße der NMR und MRT) um mehrere Größenordnungen zu verstärken (Hyperpolarisierung). Dabei wird der reine Zustand genutzt, um die Spin-Ordnung auf ein Zielmolekül zu übertragen. Der Effekt wurde von Bowers und Weitekamp entdeckt und „PASADENA“ (engl. Parahydrogen And Synthesis Allow Dramatically Enhanced Nuclear Alignment) genannt. Heute wird die Methode häufig als „PHIP“ (engl. ParaHydrogen Induced Polarization) bezeichnet. Die Methode wurde verwendet, um Abläufe von Hydrierungsreaktionen zu untersuchen. Aktuelle Forschungen zielen auf die Entwicklung von neuartigen MRT-Kontrastmitteln ab.
Ortho- und Parawasser
Wie beim H2-Molekül kann man auch beim Wassermolekül (H2O) einen Ortho- und einen Para-Zustand unterscheiden, je nachdem, ob die Spins der Wasserstoffkerne parallel oder antiparallel sind. (Der Sauerstoffkern hat, außer im Fall des sehr seltenen Isotops 17O, keinen Spin.) Durch quantenmechanische Effekte sind die Rotationszustände des Moleküls mit dem Kernspin verknüpft: Der Grundzustand von Para-Wasser hat die Rotationsquantenzahl j=0, der von Ortho-Wasser die Rotationsquantenzahl j=1. Para und Ortho-Wasser konnten mit Hilfe starker elektrischer Felder getrennt werden und es konnte nachgewiesen werden, dass die beiden Formen des Wassers unterschiedliche chemische Eigenschaften haben: Die Reaktion mit dem Diazenylium-Ion
verläuft bei Para-Wasser um 23±9 % schneller als bei Ortho-Wasser.
Siehe auch
Heliumatom: mit Ortho- und Parahelium als analogen Zuständen


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 07.12. 2025