
V-Lambda-Kurve
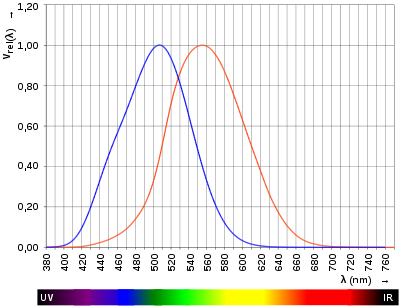
Die Hellempfindlichkeitskurve (auch: der relative spektrale
Hellempfindlichkeitsgrad)
beschreibt die spektrale Hell-Empfindlichkeit des menschlichen Auges bei
Tageslicht (photopischer
Bereich).
Hellempfindlichkeitsgrad
Elektromagnetische Strahlung im Wellenlängenbereich von etwa 380 bis 780 Nanometern (also im „sichtbaren Spektralbereich“) löst im menschlichen Auge eine Helligkeitsempfindung aus – diese Strahlung wird als Licht wahrgenommen. Das Auge ist jedoch nicht überall in diesem Bereich gleich empfindlich. Auf Wellenlängen am Rand des sichtbaren Bereiches ist eine höhere Strahlungsintensität nötig, um dieselbe Helligkeitsempfindung zu bewirken als in der Mitte des sichtbaren Bereiches.
Die Empfindlichkeit des Auges bei der Wellenlänge
wird beschrieben durch das pektrale
photometrische Strahlungsäquivalent
.
Die Kurve
gibt beispielsweise an, welche spektrale Leuchtdichte
bei der Wellenlänge
wahrgenommen wird, wenn eine bestimmte spektrale Strahldichte
in das Auge fällt, oder welche spektrale Lichtstärke
bei der Wellenlänge
erzielt wird, wenn eine bestimmte spektrale Strahlstärke
vorliegt. Allgemein stellt
den Zusammenhang zwischen den photometrischen
Größen und den zugehörigen radiometrischen
Größen her.
Es ist üblich, die -Kurve
zu schreiben als
,
sie also zu zerlegen in das Produkt aus
- dem Zahlenwert
, den sie in ihrem Maximum annimmt (den „Maximalwert des photometrischen Strahlungsäquivalents“) und
- der zwischen 0 und 1 variierenden Kurve
, welche den Verlauf der Empfindlichkeit für verschiedene Wellenlängen relativ zum Kurvenmaximum beschreibt (dem „relativen spektralen Hellempfindlichkeitsgrad“).
Tagessehen
Die -Kurve
wurde empirisch ermittelt, 1924 im „Internationalen Standard Beobachter“
veröffentlicht (Internationale Beleuchtungskommission, Commission Internationale de l'Éclairage, CIE) und
1983 in der CIE (CIE 018.2-1983 )
überarbeitet. Sie ist im Bereich 360 nm bis 830 nm in 1-nm-Schritten
für einen 2°-Standardbeobachter definiert. Die Werte von
gelten also nur für eine Beobachtung in einem 2° großen Gesichtsfeld, was dem zentralen Bereich des
scharfen Sehens beim Menschen entspricht. In Deutschland
ist sie unter DIN 5031 normiert.
Das Maximum der -Kurve
liegt bei 555 nm.
Wird die -Kurve
mit dem Faktor
multipliziert, ergibt sich das spektrale photometrische Strahlungsäquivalent für
Tagessehen
.
Dämmerungs- und Nachtsehen
Für das Dämmerungssehen (mesopischer
Bereich) wurde die -Kurve
und für das Nachtsehen (skotopischer
Bereich) die
-Kurve
definiert. Diese erlangen zum Beispiel im Rahmen der Blendungsbewertung bei
Automobilscheinwerfern im Dunkeln immer mehr an Bedeutung. Die spektrale
Verschiebung zwischen Tag- und Nachtsehen wird als Purkinje-Effekt
bezeichnet.
Das Maximum der -Kurve
liegt bei 507 nm.
Wird die -Kurve
mit dem Faktor
multipliziert, ergibt sich das spektrale photometrische Strahlungsäquivalent für
Nachtsehen
.
Hellempfindlichkeitskurve und Umwelt

Die Hellempfindlichkeit des menschlichen Auges liegt im Schwerpunkt des terrestrischen Sonnenspektrums. Vermutlich spielt auch eine von Pflanzen geprägte, grüne Umgebung eine Rolle. Insbesondere bei Mondlicht und in (algenreichem) Wasser ist der blaugrüne Spektralbereich von Bedeutung. Die Augen der Säugetiere ähneln denen des Menschen. Allerdings ist das Farbsehen von Tieren wenig erforscht.
Vögel und Insekten können jedoch besonders im violetten und sogar auch im nahen ultravioletten Spektralbereich sehen.
Sehempfindlichkeits-Zelltypen von Menschen und Tieren: Trichromat, Tetrachromat, Stäbchen (Auge), Zapfen (Auge).
Siehe auch


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 05.09. 2024