Airy-Formel

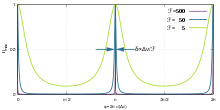
Die Airy-Formel gibt die Transmission eines Fabry-Pérot Interferometers (FPI) an. Für höhere Finessen ${\mathcal {F}}$ wird nicht-resonantes Licht besser unterdrückt. Die Linienbreite $\delta$ ist für große Finessen näherungsweise ${\frac {\Delta \nu }{\mathcal {F}}}$ mit dem Freien Spektralbereich $\Delta\nu$ .

Die Airy-Formel, benannt nach dem Mathematiker und Astronom George Biddell Airy, gibt den Verlauf der transmittierten Intensität elektromagnetischer Strahlung in einem Fabry-Pérot-Interferometer an, in Abhängigkeit vom Verhältnis der Wellenlänge oder Frequenz der Strahlung zum freien Spektralbereich des Interferometers.

Die Airy-Formel ergibt sich, wenn man die elektrischen Felder aller im Interferometer umlaufenden Teilwellen phasen- und amplitudenrichtig addiert.

Herleitung

Die Intensität der im Interferometer umlaufenden Strahlen ist proportional zur transmittierten Intensität. Bei der Berechnung muss die nicht-ideale Reflexion an den beiden Endspiegeln mit dem Amplituden-Reflexionskoeffizienten $r\neq 1$ berücksichtigt werden. Er ist über $r^{2}+t^{2}=1$ mit dem Amplituden-Transmissionskoeffizienten verknüpft. Nach Umläufen, also Reflexionen, ist der Betrag des elektrischen Feldes um den Faktor $r^{2m}$ kleiner.

Während eines Umlaufs, d.h. wenn eine Teilwelle das Interferometer einmal hin und zurück durchlaufen hat, akkumuliert diese einen Phasenwinkel $2\varphi$ (also $1\varphi$ pro zurückgelegter Resonatorlänge ). Diese Phase hängt ab

vom Verhältnis der Resonatorlänge zur Wellenlänge $\lambda$ des Lichts sowie
vom Brechungsindex des Mediums zwischen den Endspiegeln.

Dies lässt sich auch ausdrücken als Verhältnis von Lichtfrequenz $\nu$ zum freien Spektralbereich $\Delta \nu ={\frac {c}{2nL}}$ (Einheit Frequenz) des Fabry-Pérot-Interferometers:

$\varphi =n{\frac {2\pi L}{\lambda }}=2\pi {\frac {\nu }{\Delta \nu }}=-2\pi {\frac {\lambda }{\Delta \lambda }}$

Die elektrische Feldstärke im Innern des Resonators ist

${\begin{aligned}E&=E_{\mathrm {i} }t\left(1+\sum _{m=1}^{m=\infty }r^{2m}\exp \left(2im\varphi \right)\right)\\&=E_{\mathrm {i} }{\frac {\sqrt {1-r^{2}}}{1-r^{2}\exp \left(2i\varphi \right)}}\end{aligned}}$

mit der Feldstärke $E_{i}$ des einfallenden Lichts.

In der obigen Rechnung wurde nach einer Indexverschiebung die geometrische Reihe ausgewertet. Das Betragsquadrat dieses Ausdrucks ergibt mit verschiedenen trigonometrischen Identitäten die Airy-Formel:

${\begin{aligned}I=E\cdot E^{*}&={\frac {I_{\mathrm {i} }}{1-R}}\cdot {\frac {1}{1+\left({\frac {2{\sqrt {R}}}{1-R}}\right)^{2}\sin ^{2}(\varphi )}}\\&={\frac {I_{\mathrm {max} }}{1+\left({\frac {2{\mathcal {F}}}{\pi }}\right)^{2}\sin ^{2}(\varphi )}}\end{aligned}}$

In dieser Intensitätsdarstellung werden verwendet:

der Reflexionskoeffizient $R=r^{2}$
der Transmissionskoeffizient $T=t^{2}$
die Finesse ${\mathcal {F}}={\frac {\pi {\sqrt {R}}}{1-R}}$ .

Siehe auch

Fresnelsche Formeln

Basierend auf einem Artikel in:

Wikipedia.de