
Erlang-Verteilung
Die Erlang-Verteilung ist eine stetige Wahrscheinlichkeitsverteilung, eine Verallgemeinerung der Exponential-Verteilung und ein Spezialfall der Gamma-Verteilung. Sie wurde von Agner Krarup Erlang für die statistische Modellierung der Intervall-Längen zwischen Telefonanrufen entwickelt.
Die Erlang-Verteilung wird in der Warteschlangentheorie verwendet, um die Verteilung der Zeitspanne zwischen Ereignissen eines Poisson-Prozesses, beispielsweise der Ankunft von Kunden, zu erfassen, sowie in der Qualitätssicherung zur Beschreibung von Lebensdauern. In Callcentern wird diese Verteilung für die Personaleinsatzplanung genutzt, um die Anzahl der benötigten Agents auf Grund des erwarteten Anrufvolumens im Zeitintervall zu bestimmen.
Die Erlang-Verteilungsdichte liefert die Verteilung der Wahrscheinlichkeit
dafür, dass nach Verstreichen des Orts- oder Zeitabstands
das
-te
Ereignis eintritt, wenn man
Ereignisse pro Einheitsintervall erwartet (siehe Herleitung).
Sie beschreibt eine Kette von
nacheinander erfolgenden Ereignissen. Der wahrscheinlichste Abstand bis zum
-ten
Ereignis (Modus)
ist kleiner als der Mittelwert (Erwartungswert),
weil kürzere Ereignisabstände häufiger auftreten. Füllt man die der Größe nach
sortierten Abstände der jeweiligen Einzelereignisse in ein Histogramm, so zeigt dieses
dementsprechend eine Exponential-Verteilung.
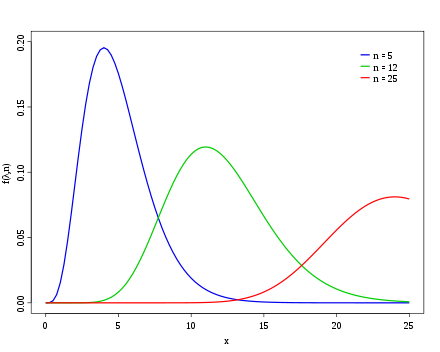
Definition
Die Erlang-Verteilung
mit den Parametern
(einer positiven reellen
Zahl) und
(einer natürlichen
Zahl) ist eine spezielle Gammaverteilung,
die durch die Dichtefunktion
festgelegt wird, und die sich von der allgemeinen Gammaverteilung durch die Beschränkung auf natürliche Zahlen im zweiten Parameter unterscheidet.
Für eine Erlang-verteilte Zufallsvariable
ist die Wahrscheinlichkeit, dass
innerhalb des Intervalls
liegt, durch die Verteilungsfunktion
gegeben, wobei
bzw.
die unvollständige
Gammafunktion bezeichnet.
Herleitung und Interpretation
Die Erlang-Verteilung kann interpretiert werden als die
Wahrscheinlichkeitsdichte, nach einer Zeit
das
-te
Ereignis zu erhalten. Dabei seien die Ereignisse poissonverteilt.
Betrachten wir die Wahrscheinlichkeit, dass das -te
Ereignis im Zeitintervall
ist. Dies ist offensichtlich die Wahrscheinlichkeit, dass
Ereignisse im Intervall
sind, multipliziert mit der Wahrscheinlichkeit, dass genau ein Ereignis in
ist. Da die Ereignisse poissonverteilt
und unabhängig in disjunkten Intervallen sind, ist dies:
.
Dies ist in erster Ordnung :
,
so dass sich die Erlang-Verteilung ergibt als:
.
Eigenschaften
Da eine Erlang-verteilte Zufallsvariable
die Summe von
unabhängig und identisch mit Parameter
exponentialverteilten
Zufallsvariablen
ist, ergeben sich die folgenden Eigenschaften.
Erwartungswert
Die Erlang-Verteilung besitzt den Erwartungswert
Varianz
Analog ergibt sich die Varianz zu
Modus
Der Modus, das Maximum der Dichte, liegt bei
Charakteristische Funktion
Aus der charakteristischen Funktion einer exponentialverteilten Zufallsvariablen erhält man die einer Erlang-verteilten Zufallsvariable:
Momenterzeugende Funktion
Analog ergibt sich für die momenterzeugende Funktion
Entropie
Die Entropie der Erlang-Verteilung beträgt
wobei ψ(p) die Digamma-Funktion bezeichnet.
Beziehungen zu anderen Verteilungen
Beziehung zur Exponentialverteilung
- Die Erlang-Verteilung
ist eine Verallgemeinerung der Exponentialverteilung, denn sie geht für
in diese über
.
- Es seien
viele, alle mit dem gleichen Parameter
exponentialverteilte Zufallsvariablen
, die stochastisch unabhängig sind, gegeben. Dann ist die Zufallsvariable
Erlang-verteilt mit den Parametern
und
.
Beziehung zur Poisson-Verteilung
- Für einen Poisson-Prozess
wird die zufällige Anzahl der Ereignisse bis zu einem definierten Zeitpunkt
mittels Poisson-Verteilung
bestimmt, die zufällige Zeit bis zum
-ten Ereignis ist Erlang-verteilt. Im Fall
geht diese Erlang-Verteilung in eine Exponentialverteilung über, mit der die Zeit bis zum ersten zufälligen Ereignis sowie die Zeit zwischen zwei aufeinanderfolgenden Ereignissen bestimmt werden kann.
- Die Erlang-Verteilung ist die zur Poisson-Verteilung konjugierte Verteilung.
Beziehung zur stetigen Gleichverteilung
Eine Erlang-Verteilung kann als Faltung
von
gleichmäßig
stetig verteilten Funktionen
erzeugt werden:
Beziehung zur Gamma-Verteilung
Die Erlang-Verteilung mit dem Parameter
und
Freiheitsgraden entspricht einer Gammaverteilung mit natürlichem Formparameter
(und inversem Skalenparameter
).


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 13.11. 2025