Ränderung
Als Ränderung (engl.: Bordering Method) bezeichnet man ein Verfahren zur Verbesserung der Lösungseigenschaften linearer Gleichungssysteme. Das Verfahren kommt in der linearen Algebra und der Numerik zur Anwendung.
Einem linearen Gleichungssystem
mit singulärer
oder schlecht konditionierter
Systemmatrix
kann man durch Hinzufügen von Zeilen und Spalten zu
und entsprechendes Vergrößern von
und
ein erweitertes lineares Gleichungssystem zuordnen, bei dem die Systemmatrix gut
konditioniert (also auch regulär) ist. Die einfachen Beispiele in den nächsten
zwei Abschnitten sollen das verdeutlichen. Die durch Zeilen und Spalten ergänzte
Systemmatrix bezeichnet man auch als geränderte Matrix.
Beispiel (Regularisierung)
Gegeben sei das Gleichungssystem
mit der -Systemmatrix
,
dem Einervektor
der Unbekannten und der rechten Seite
.
Dieses kann durch Ränderung der Systemmatrix mit der Spalte
und der Zeile
regularisiert werden:
Die zu dem ursprünglichen System hinzugekommenen Einträge sind überstrichen.
Das geränderte System hat die eindeutige Lösung
mit
.
Davon ist die durch die Ränderung dem ursprünglichen Problem zugeordnete Lösung
.
Die Größe von
drückt aus, wie stark der regularisierende Einfluss der Ränderung ist.
Beispiel (Verbesserung der Kondition)
In diesem Beispiel sei
ein bzgl. der euklidischen Norm mit 10 % Fehler behafteter Messwertvektor
aus dem mit Hilfe der Gleichung
die Größen
ermittelt werden sollen. Für
ergibt sich die Lösung
Für die um ca 10 % abweichende (also innerhalb der Fehlertoleranz
liegende) rechte Seite
ermittelt man die vollkommen andere Lösung
.
Ein Maß dafür, wie stark sich relative Fehler
in der Messung auf den relativen Fehler
des Rechenergebnisses auswirken, ist die Kondition
der Systemmatrix
Für die spezielle Wahl von
aus diesem Beispiel ergibt sich
.
Relative Fehler in den Messdaten
können sich also durch die schlechte Kondition der Matrix
ca. hundertfach im relativen Fehler der aus diesen Daten berechneten
Größen
niederschlagen.
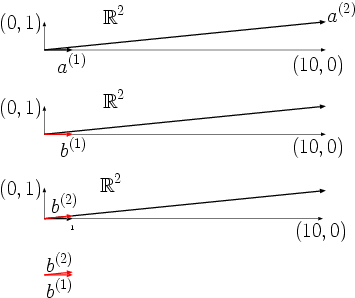
Dieser Effekt ist im folgenden Bild für die oben vorgegebenen rechten Seiten
grafisch veranschaulicht. Aus dem oberen Teil des Bildes erkennt man, dass die
zwei Spaltenvektoren
und
von
beinahe linear abhängig voneinander sind.
Dadurch fallen die im unteren Teil des Bildes rot dargestellten zwei rechten
Seiten
und
,
die sehr nahe beieinander liegen, in die Bildräume unterschiedlicher Spalten von
und die Koeffizienten
in
unterscheiden sich beim Wechsel von
zu
stark voneinander.
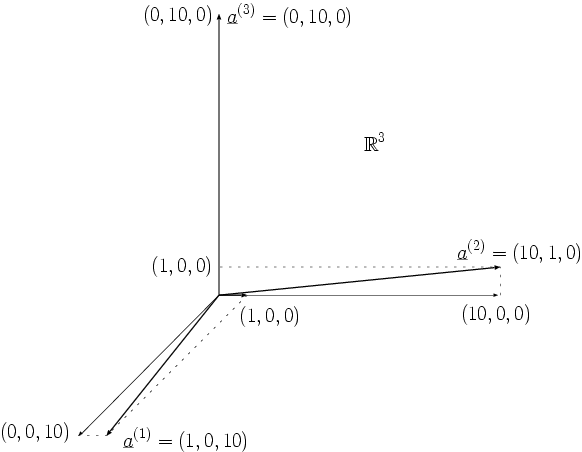
Effekt einer Ränderung: Das Hinzufügen einer zusätzlichen Zeile zu
entspricht der Erweiterung des Wertebereiches von
um eine Dimension vom
zum
und mit dem Ergänzen einer Spalte kommt ein neuer Spaltenvektor
hinzu. Durch geschickte Wahl der zusätzlichen Komponenten
und des zusätzlichen Spaltenvektors
erreicht man, dass die Spaltenvektoren der geränderten Matrix
wesentlich besser voneinander separiert werden. Genauer wählt man die neuen
Freiheitsgrade möglichst so, dass die Spalten
der geränderten Matrix
senkrecht aufeinander stehen und die gleiche Länge haben.
Im Beispiel erreicht man das näherungsweise mit der Ränderung
Die Lage der Spaltenvektoren der geränderten Matrix
im
ist im folgenden Bild veranschaulicht.
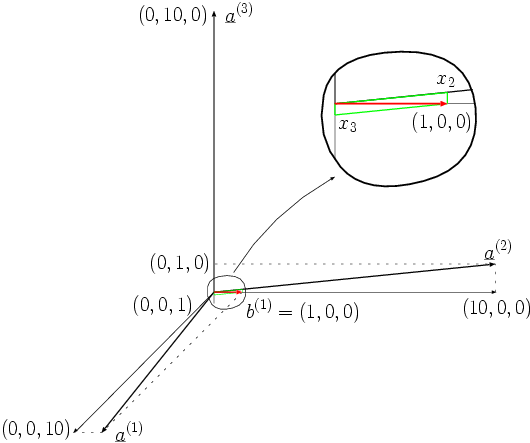
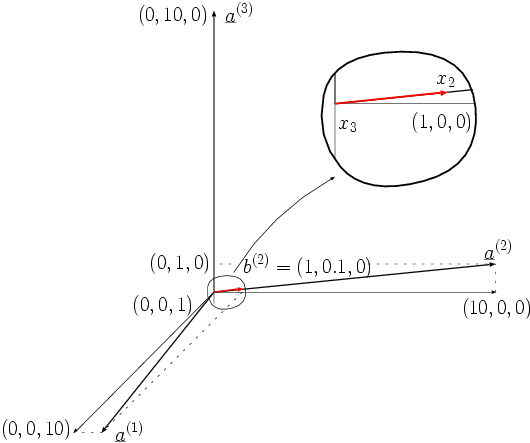
Für das geränderte System
ergeben sich mit den geränderten rechten Seiten
und
jeweils die Lösungen
bzw.
.
Die für die Messaufgabe wesentlichen Komponenten
und
ändern sich also durch die 10 %ige Störung von
überhaupt nicht.
Das ist in den folgenden zwei Bildern noch einmal veranschaulicht.
Die Konditionszahl der geränderten Matrix hat sich auf
verringert. Der relative Fehler wird sich durch die Berechnung von
aus den Messwerten
also nur noch höchstens um ca. 15 % verschlechtern.
In diesem motivierenden Beispiel wurde die Ränderung sehr einfach gehalten.
Durch eine geschicktere Wahl der Ränderung ist erreichbar, dass sich der
relative Fehler durch die Berechnung von
aus
überhaupt nicht mehr verschlechtert, dass also
gilt.
Regularisierung
Sei
eine reelle
-Matrix
und
ein dazu passender
-dimensionaler
Spaltenvektor. Eine geränderte Matrix
mit passenden Matrizen
und
ist genau dann regulär, wenn die Zeilen von
eine Basis des Kerns von
bilden und die Spalten von
ein minimales System von Spalten ist, das zusammen mit den Spalten von
den
aufspannt. In diesem Fall lässt sich das geränderte System
eindeutig lösen und die Dimension der (quadratischen) geränderten Matrix ist
(hierbei ist
der Defekt
von
).
Je nach Wahl der Matrizen
und
kann man verschiedene Aufgaben lösen. Spannen zum Beispiel die Zeilen von
den Kern
von
auf und die Spalten von
das orthogonale
Komplement des Bildes von
,
so ist
aus der Lösung des geränderten Gleichungssystems gerade
mit der Pseudoinversen
von
.
Den Kern von
kann man mit Hilfe des Gaußschen
Eliminationsverfahrens berechnen und das orthogonale Komplement des Bildes
von
berechnet man günstigerweise als Kern von
.
Optimale Ränderung
Die Idee aus dem letzten Abschnitt wird hier aufgegriffen und eine beliebige
Matrix
so gerändert, dass die Spalten der erweiterten Matrix
alle senkrecht aufeinander stehen und die gleiche euklidische Norm
haben. Die erweiterte Matrix
ist dann das Produkt des größten Singulärwertes
von
mit einer orthogonalen Matrix und hat damit die minimal mögliche Konditionszahl
eins.
Singulärwertzerlegung als Hilfsmittel zur Ränderung
Die Struktur der Systemmatrix kann man mit Hilfe einer aus der Singulärwertzerlegung
von
gewonnenen Koordinatentransformation
,
vereinfachen. Die neue Systemmatrix
hat dann sehr viele Nulleinträge. Nur die Elemente
sind mit Nichtnullelementen, nämlich den Singulärwerten
,
belegt. Hierbei ist
der Rang der Matrix
.
Die Transformationsmatrizen
und
sind orthogonal und damit normerhaltend
,
.
Daraus folgt, dass die transformierte Systemmatrix
die gleiche Kondition hat, wie die originale Systemmatrix
.
Eine Erweiterung
der Matrix
um Matrixblöcke (zueinander passender Dimensionen)
entspricht eine Ränderung der Matrix
,
wenn man die Transformationsmatrizen
und
passend durch Teile der Einheitsmatrix
ergänzt:
Die erweiterten Transformationsmatrizen
und
sind wieder orthogonal, womit die Kondition der erweiterten Systemmatrix
mit der der Matrix
übereinstimmt.
Im Folgenden brauchen also nur noch Matrizen untersucht werden, die eine Systemmatrix mit der (von der Singulärwertzerlegung her bekannten) Struktur
mit einer ganzen Zahl
haben.
Ergänzung einer rechteckigen Matrix zu einer quadratischen
Hier wird nur die Ränderung von Matrizen mit mehr Zeilen als Spalten
beschrieben ().
Durch Transposition kann man die Aussagen auf Matrizen mit mehr Spalten als
Zeilen übertragen. Mit den Aussagen aus dem vorhergehenden
Abschnitt ist klar, dass man sich auf die Untersuchung von Matrizen der Form
beschränken kann, wobei
eine positiv semidefinite
Diagonalmatrix und
eine Nullmatrix mit der gleichen
Anzahl an Spalten wie
ist. Zunächst wird vorausgesetzt, dass
keine Nullmatrix ist. Das maximale Diagonalelement
von
ist also größer null. Dann ist es günstig, die fehlenden Spalten durch die an
diese Spaltenpositionen gehörigen Spalten der mit
skalierten Einheitsmatrix zu ergänzen:
Falls
regulär ist, trifft das auch für die geränderte Matrix
zu. Man hat also die Matrix in diesem Falle regularisiert.
Nachdem man die Rechteckmatrix so zu einer quadratischen ergänzt hat, kann
man die im nächsten Abschnitt beschriebene Ränderung benutzen, um die Matrix
besser zu konditionieren (oder, falls
singulär ist, zu regularisieren). Dort wird sich herausstellen, dass die Wahl
von
als Skalierungsfaktor günstig ist, da man die Norm dieser Spalten dann nicht
mehr künstlich durch eine Ränderung vergrößern muss.
Optimale Ränderung einer quadratischen Matrix
Im vorhergehenden Abschnitt wurde beschrieben, wie man eine rechteckige Matrix durch Ränderung günstig zu einer quadratischen ergänzen kann. Hier wird nun darauf eingegangen, wie sich die Kondition einer quadratischen Matrix verbessern oder im singulären Fall die Matrix regularisieren lässt.
Der Unterabschnitt zur Singulärwertzerlegung
zeigt, dass man sich dabei auf die Ränderung von Diagonalmatrizen
beschränken kann.
Die Spaltenvektoren der Matrix
stehen bereits senkrecht aufeinander. Man muss sie nur noch geeignet verlängern,
damit sie normgleich werden. Dabei fängt man mit dem letzten Spaltenvektor an,
dessen Komponente
den kleinsten Wert der Diagonalelemente von
hat. Zunächst ergänzt man
durch eine Zeile
,
was einer Erweiterung des Spaltenvektorraumes um eine Dimension entspricht (der
Punkt
steht hier als Stellvertreter für den Spaltenindex). In dieser zusätzlichen
Dimension verlängert man den letzten Spaltenvektor der erweiterten Matrix so
weit, dass er die gleiche euklidische Länge wie der erste (längste)
Spaltenvektor von
bekommt (also die Länge
):
Die Spaltenvektoren der erweiterten Matrix
bleiben dadurch orthogonal zueinander. Um wieder eine quadratische Matrix zu
erhalten, muss man noch eine Spalte
ergänzen. Dazu wählt man günstigerweise eine Spalte mit
Die Spalte
hat die gewünschte Norm
und steht wiederum senkrecht auf allen anderen Spalten der erweiterten Matrix
.
Durch analoges Ergänzen weiterer Zeilen und Spalten kann man sukzessive die Norm aller Spaltenvektoren der erweiterten Matrix angleichen. Wie gewünscht, ist das Ergebnis eine Systemmatrix, deren Spalten alle orthogonal aufeinander stehen und die gleiche Norm haben.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 15.03. 2023