Ring (Mengensystem)
Ein Mengenring, auch einfach kurz Ring oder seltener Boole'scher Ring genannt, ist in der Maßtheorie ein spezielles Mengensystem und somit eine Menge von Mengen. Ringe und ihre Erweiterungen zu komplexeren Mengensystemen wie σ-Algebren spielen eine wichtige Rolle in dem axiomatischen Aufbau der Wahrscheinlichkeitstheorie und der Integrationstheorie.
Felix Hausdorff nannte aufgrund einer Ähnlichkeit zur algebraischen Struktur eines Ringes in der algebraischen Zahlentheorie einen Mengenverband „Ring“. Unter einem Ring versteht man heute in der Maßtheorie üblicherweise lediglich die hier definierten Mengensysteme.
Der hier verwendete Begriff des Ringes unterscheidet sich außerdem von dem eines Rings im Sinne der Algebra, beide stehen aber in einem Zusammenhang.
Definition
Sei
eine beliebige Menge. Ein Mengensystem
auf
,
also eine Menge von Teilmengen von
heißt ein Mengenring oder Ring über
,
wenn folgende Eigenschaften erfüllt sind:
: Der Ring enthält die leere Menge.
(Stabilität/Abgeschlossenheit bezüglich endlicher Vereinigung).
(Stabilität/Abgeschlossenheit bezüglich Differenz).
Äquivalent dazu ist, dass
ein Ring
im Sinne der Algebra mit Addition
und Multiplikation
ist. Hierbei bezeichnet
die symmetrische
Differenz.
Weitere äquivalente Definitionen befinden sich im entsprechenden unten stehenden Abschnitt.
Beispiele
Über jeder beliebigen Menge
ist
der kleinste mögliche Ring, denn er enthält die leere Menge, die Vereinigung der
leeren Menge mit sich selbst ergibt wieder die leere Menge und die Differenz der
leeren Menge und der leeren Menge ist ebenfalls die leere Menge.
Die Potenzmenge
ist der größte mögliche Mengenring, denn die Potenzmenge ist stabil bezüglich
allen Mengenoperationen, da sie per Definition alle Teilmengen der Obermenge
enthält.
Ist
eine beliebige Menge, so ist das System aller endlichen Teilmengen, also
ein Ring. dabei bezeichnet
die Mächtigkeit
der Menge
(Es gilt
und die leere Menge ist in jeder Menge enthalten). Dass
ein Ring ist, folgt aus der Tatsache, dass Vereinigungen und Differenzen
endlicher Mengen wieder endlich sind.
Ein in der Anwendung wichtiger Ring auf
ist
Er besteht aus Mengen, die sich als endliche Vereinigungen von halboffenen
Intervallen in
darstellen lassen und ist somit genau der von dem Halbring
erzeugte
Ring.
Eigenschaften
Stabilität bezüglich Mengenoperationen
Jeder Mengenring ist abgeschlossen bezüglich der Bildung der symmetrischen
Differenz ,
denn es ist
.
Daher ist ein Ring wegen
auch abgeschlossen bezüglich Durchschnittbildung.
Daraus folgt jeweils induktiv,
dass auch jede endliche Vereinigung und jeder nicht leere, endliche Durchschnitt
von Elementen des Mengenringes
in ihm enthalten ist, d.h. für alle
gilt:
- Sind
, so ist auch
- Sind
, so ist auch
Beziehung zu Ringen im Sinne der Algebra
Das Tripel
mit dem Mengenring
ist ein Ring
im Sinne der Algebra, wobei
und
für alle
(Stabilität/Abgeschlossenheit bezüglich symmetrischer
Differenz und Durchschnitt).
Die leere Menge
entspricht dem Nullelement
und
dem Einselement.
Ein Mengenring muss ein Nullelement enthalten, muss aber nicht ein Einselement
enthalten. Ist umgekehrt
ein Mengensystem, so dass
ein Ring im Sinne der Algebra ist, dann ist
wegen
und
für alle
auch immer ein Mengenring. Damit sich jeder Mengenring
als Ring im Sinne der Algebra darstellen lässt, darf
nicht leer sein, denn die leere Menge
kann kein Nullelement enthalten und daher keine Trägermenge eines Ringes im
Sinne der Algebra sein.
Äquivalente Definitionen
Wenn
ein System von Teilmengen von
ist und wenn
Mengen sind, dann sind wegen
und
folgende zwei Aussagen äquivalent:
und falls
auch
Ist außerdem ,
so sind wegen
und
sowie
für jede Menge
mit
ebenso äquivalent:
ist ein Mengenring.
ist ein Mengenverband und es gilt:
ist ein Mengenhalbring und es gilt:
und
ist eine abelsche Gruppe und
ist eine Halbgruppe.
ist ein Ring im Sinne der Algebra mit Addition
und Multiplikation
.
ist ein idempotenter (kommutativer) Ring im Sinne der Algebra.
und
und falls
existiert ein
mit
und es existiert ein
mit
Operationen mit Ringen
Schnitte von Ringen
Schnitte von zwei Ringen
und
,
also das Mengensystem
,
sind stets wieder Ringe. Denn sind exemplarisch ,
so ist
in
, da
auch in
sind.
in
, da
auch in
sind.
Somit ist
auch in
,
der Schnitt ist also stabil bezüglich Vereinigung von Mengen. Die Stabilität
bezüglich der Differenzbildung folgt analog.
Die Aussage gilt ebenso für den Schnitt einer beliebigen Anzahl von Ringen,
da sich die obige Argumentation dann auf alle dieser Ringe ausweiten lässt.
Somit gilt: ist
eine beliebige Indexmenge und sind
Ringe, die alle auf derselben Grundmenge
definiert sind, so ist der Schnitt aller dieser Ringe wieder ein Ring
:
.
Vereinigung von Ringen
Die Vereinigung zweier Ringe
und
,
also das Mengensystem
ist im Allgemeinen kein Ring mehr. Betrachtet man beispielsweise die beiden Ringe
sowie
,
so ist
.
Dieses Mengensystem ist aber weder vereinigungsstabil, da es
nicht enthält, noch ist es differenzstabil, da es
nicht enthält, und somit auch kein Ring.
Produkte von Ringen
Sind
und
Mengensysteme auf
und
und wird das Produkt von
und
definiert als
,
so ist das Produkt von zwei Ringen im Allgemeinen kein Ring mehr, sondern lediglich ein Halbring. Betrachtet man als Gegenbeispiel den Ring
,
so enthält das Mengensystem
sowohl die Mengen
als auch
.
Die Menge
ist jedoch nicht in
enthalten, da sie sich nicht als kartesisches
Produkt zweier Mengen aus
darstellen lässt. Somit ist das Produkt nicht stabil bezüglich
Differenzenbildung und damit auch kein Ring.
Definiert man das Produkt von Mengensystemen als
,
so ist das Produkt zweier Mengenringe
und
wieder ein Ring, der dann auf der Grundmenge
definiert ist.
Er ist genau das Tensorprodukt
der beiden Ringe, ebenso ist er der von
erzeugte
Ring.
Spur eines Rings
Die Spur
eines Rings
bezüglich einer Menge
,
also das Mengensystem
ist immer ein Ring, unabhängig von der Wahl von .
Der erzeugte Ring
Da beliebige Schnitte von Ringen wieder Ringe sind lässt sich der Hüllenoperator
definieren. Er ist per Definition der kleinste Ring, der das Mengensystem
enthält und wird der von
erzeugte Ring genannt.
Teilweise kann der erzeugte Ring direkt angegeben werden. So ist der von
einem Halbring
erzeugte Ring von der Form
,
ein explizites Beispiel dieser Form ist der Ring
im Abschnitt Beispiele.
Ebenso gilt für die oben besprochenen Produkte von Ringen
.
Verwandte Mengensysteme
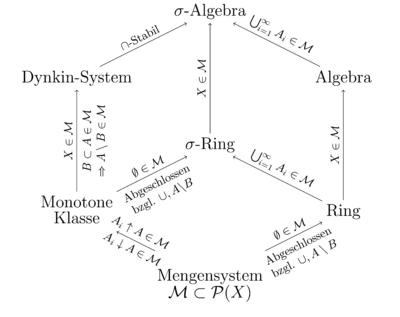
Aufbauende Begriffe
- Ein Ring, der abgeschlossen bezüglich abzählbare vielen Schnitten ist, wird ein δ-Ring genannt.
- Ein Ring, der abgeschlossen bezüglich abzählbare vielen Vereinigungen ist, wird ein σ-Ring genannt.
- Ein Ring über
, der die Grundmenge
enthält, wird eine Mengenalgebra über
genannt. Somit ist jede Mengenalgebra ein Ring, aber nicht jeder Ring eine Mengenalgebra.
Mengenverbände
Jeder Ring ist ein Mengenverband. Umgekehrt ist jeder differenzstabile Mengenverband ein Ring.
Halbringe
Jeder Mengenring ist ein Mengenhalbring, jedoch ist nicht jeder
Mengenhalbring ein Mengenring: Über der Grundmenge
ist das Mengensystem
ein Halbring, aber kein Mengenring, da es nicht Differenzstabil ist.
Monotone Klassen
Jeder Ring, der eine monotone
Klasse ist, ist ein σ-Ring (und damit auch ein δ-Ring). Denn sind die Mengen
im Ring enthalten, so ist auch
aufgrund der Eigenschaften des Ringes wieder im Mengensystem enthalten. Die
Mengen
bilden aber eine monoton
wachsende Mengenfolge, daher ist ihr Grenzwert
aufgrund der Eigenschaften der monotonen Klasse auch im Mengensystem enthalten. Das Mengensystem ist also abgeschlossen bezüglich abzählbaren Vereinigungen. Somit ist die von einem Ring erzeugte monotone Klasse immer ein σ-Ring.


© biancahoegel.de
Datum der letzten Änderung: Jena, den: 11.04. 2020